3. Случайные точки в многомерном пространстве

точек под кривой N_in к полному количеству точек N будет приближенно равно отношению площади под кривой к площади прямоугольника.

Рис. 11. Вычисление определенного интеграла статистическим моделиро­ванием.

Но площадь под кривой равна интегралу от функции f(x), поэтому

/ f{x)dx^S_{)^₎ (15)

где So = h(b — а) -площадь прямоугольника. Отметим, что метод может быть использован только в том случае, если величины h и Ь — а конечны. На рис.12 представлены результаты вычисления интеграла

1 / = / l-x² dx.

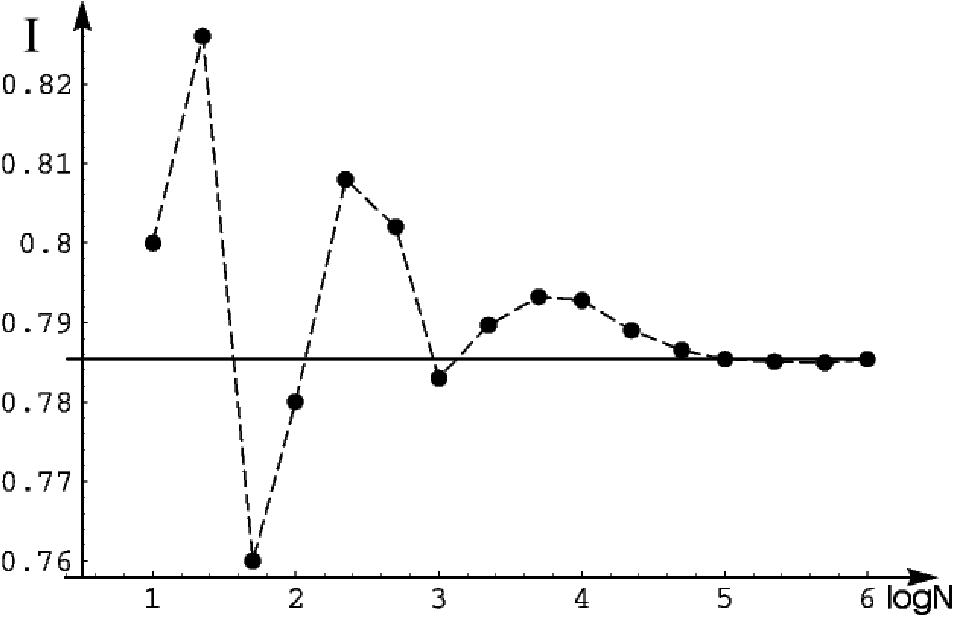
Рис. 12. Пример вычисления интеграла статистическим моделированием.

Из рис.12 видно, что с увеличением количества использованных слу-

N in чайных точек отношение —— стремится к точному значению, равному

тг/4.

Вопросы

27

Метод легко обобщается на случай многократных интегралов.

Вопросы

48. Опишите алгоритм моделирования равномерно распределенных слу­чайных точек в прямоугольнике и многомерном параллелепипеде.

49. Опишите алгоритм моделирования случайных точек, равномерно распределенных в круге и по объему шара.

50. Опишите алгоритм статистического метода вычисления площадей и объемов.

51. Опишите алгоритм статистического метода вычисления массы, по­ложения центра инерции и момента инерции тела заданной формы.

52. Опишите алгоритм статистического метода вычисления однократ­ных интегралов.

53. Предложите алгоритм статистического метода вычисления двух- и трехкратных интегралов.

Упражнения

1. Составить блок-схему и подпрограмму моделирования координат {x,y} случайных точек, равномерно распределенных в круге ради­уса R. Получить координаты нескольких точек.

2. Составить блок-схему и подпрограмму моделирования координат {x,y,z} случайных точек, равномерно распределенных по объему шара радиуса R. Получить координаты нескольких точек.

3. Составить блок-схему и подпрограмму моделирования координат случайных точек, равномерно распределенных в прямоугольнике (Ъ — а) х h и попадающих под кривую у = f(x), вписанную в пря­моугольник. Получить координаты нескольких точек.

Задачи

1. Составить программу для статистического вычисления числа тт. При­вести результаты вычислений при нескольких значениях N. Для вычисления отношения N_in/N использовать программу AVERAGE, усредняя случайную величину к , которая равна 1, если точка по­пала внутрь круга, и равна 0 для точек, не попавших в круг.

28

3. Случайные точки в многомерном пространстве

2. Составить программу для вычисления объема эллипсоида

х² у² z²

Ь ——I = 1

А² В² С²

Привести результаты вычислений при нескольких значениях N.

b

a

3. Составить программу для вычисления интеграла / = f f(x) dx.

Сравнить результаты вычислений с точным значением / для f(x) = л/1 — х² при нескольких значениях N.

54. Промоделировать равномерное распределение точек в круге радиуса R с помощью программы C-DISTRIBUTION для точек на плоско­сти.

55. Вычислить массу, положение центра инерции и момент инерции ша­ра радиуса г\ со сферической полостью радиуса Г2, (г2 < п), центр которой смещен относительно центра шара на величину d (d <r\).

Проблемы

1. Случайные точки в многомерном пространстве. Вычисление поверх­ностей и объемов тел. Вычисление определенных интегралов.

4. Неравномерно распределенные случайные числа

Случайные числа, получаемые в эксперименте, часто имеют нерав­номерное распределение. Для компьютерного моделирования статистиче­ски эквивалентных последовательностей используют несколько методов, основанных на преобразовании равномерно распределенных чисел. Неко­торые из этих методов рассматриваются ниже.

4.1. Метод функции распределения

Пусть случайные числа 7, равномерно распределенные в интервале (0,1) на оси Оу, переносятся на ось Ох с помощью монотонной функции F(x), удовлетворяющей условиям F(a) = 0, F(b) = 1 (рис.13). Легко видеть, что получаемые при этом числа х имеют неравномерное распре­деление в интервале (а, Ь) на оси Ох.

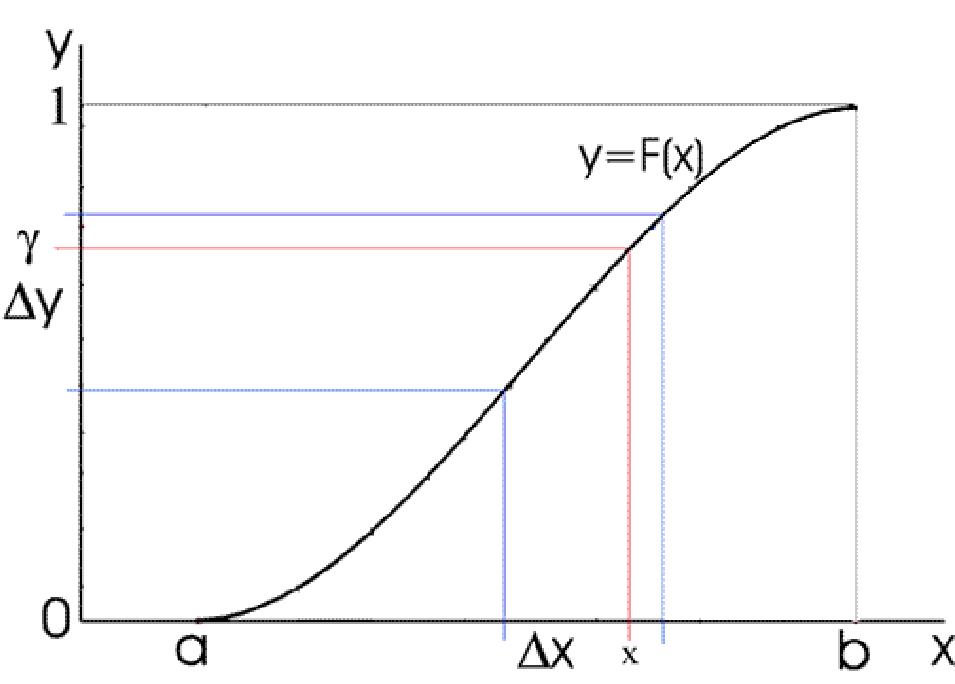
Рис. 13. Моделирование случайных чисел методом функции распределе­ния.

Плотность распределения этих чисел может быть вычислена следую­щим образом. Каждому числу 7 на оси Оу соответствует число х на оси Ох, поэтому количество чисел 7, которые попадут в интервал Ау, рав­но количеству чисел х в интервале Ах, границы которого соответствуют границам Ау :

N(x е Ах) = АГ(7 е Ау).

Но для равномерно распределенных чисел

7V(₇ е Ау) « N Ау, где N есть полное количество полученных чисел 7 , поэтому плотность

30

4. Неравномерно распределенные случайные числа

вероятности для чисел х равна

, Nix е Ах) Nh е Ay) Ay dF

w\x) « — = —— — « —- « —.

^y N Ax N Ax Ax dx

То есть для получения случайных чисел с плотностью w(x) в качестве функции F(x) на рис.13 необходимо брать такую функцию, для которой

^- = w(x)

или

F(x) = / w(x) dx. (16)

a

Такая функция F(x) называется функцией распределения случайной ве­личины х.

Из рис.13 видно, что числа 7 и ж связаны соотношением

l = F{x),

то есть

x = F-\₁),

где F-¹ - функция, обратная к F.

Для примера на рис.14 представлены результаты моделирования слу­чайных точек, распределенных по экспоненциальному закону w(x) = е~^х, О < х < оо.

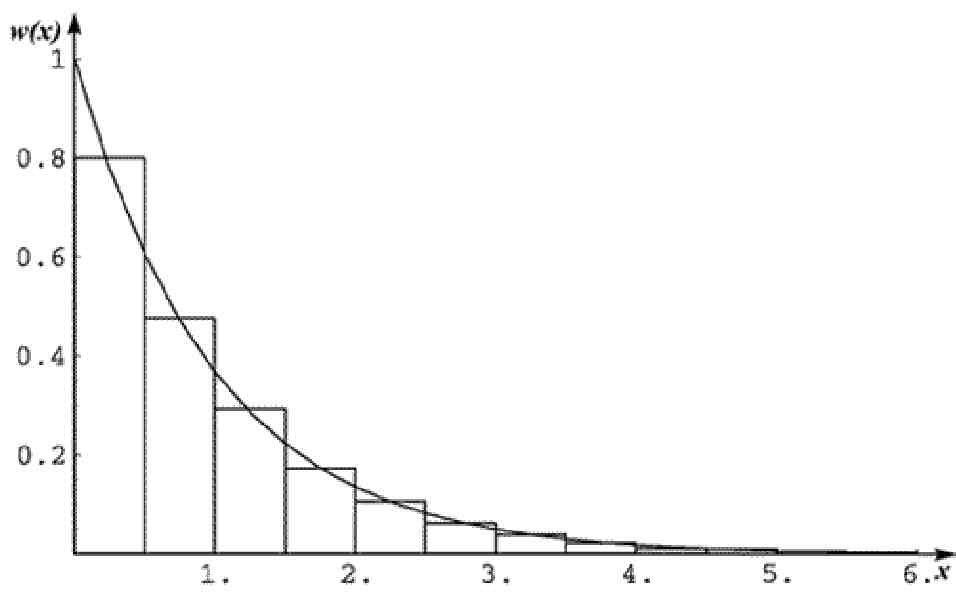
Рис. 14. Результаты моделирования экспоненциального распределения.

В этом случае

F(x) = 1-е~^х

и

z=-log(l-7).

4.1. Метод функции распределения

31

Отметим, что случайные числа 1 — 7 так же, как и числа 7, имеют равно­мерное распределение в интервале (0,1), то есть они статистически экви­валентны числам 7, поэтому при моделировании использовалась формула

z = -log7.

Еще раз об интегралах. Пусть случайные числа х выбираются из распределения w(x) на отрезке (а, Ь), для каждого из них вычисляется значение некоторой функции /(ж), и эти значения усредняются:

1 ^N

_{i=J2 /М- (17)}

г=1

Для вычисления величины / разделим область (а, Ь) на малые отрезки Axk и сумму по г преобразуем в сумму по этим интервалам, сгруппировав вклады от точек, попадающих в один интервал. Если при этом пренебречь изменением функции f(x) в интервале Ах_к, то

I~-^J2 Л^ж*) ЩхеАх_к),

к

где N(x е Ах_к)- количество случайных чисел х в интервале Ах_к. Про­стое преобразование этой суммы

к ^к

и учет формулы (3) дает

_{i ~ J2 Лж*) ад(ж*)Аж*-}

ь

f{x) w(x) dx. Это

При Дж_Л ->• 0 эта сумма станет интегралом f(x) w(x) dx. Это значит,

что формула (17) дает оценку этого интеграла.

Чтобы применить этот метод для вычисления интеграла

b

I

f{x)

dx,

32

4. Неравномерно распределенные случайные числа

где под интегралом нет второго сомножителя, преобразуем подынтеграль­ное выражение следующим образом:

_{j = ,Ш)т dx,}

w(x

где функция w˜(x) обладает свойствами плотности вероятности:

w˜(x) > 0, a ≤ x ≤ b,

w(x) dx = 1.

В соответствии с (17) оценкой интеграла I является сумма

1

I & — ^

f{Xi)

N w(xi)

где x_i-случайные числа с плотностью распределения w˜(x).

Пример такого вычисления представлен на рис.15. Для оценки инте­грала

oo

I

exp(-x²) dx

в качестве w˜(x) использовалась функция

w˜(x) = exp(-x).

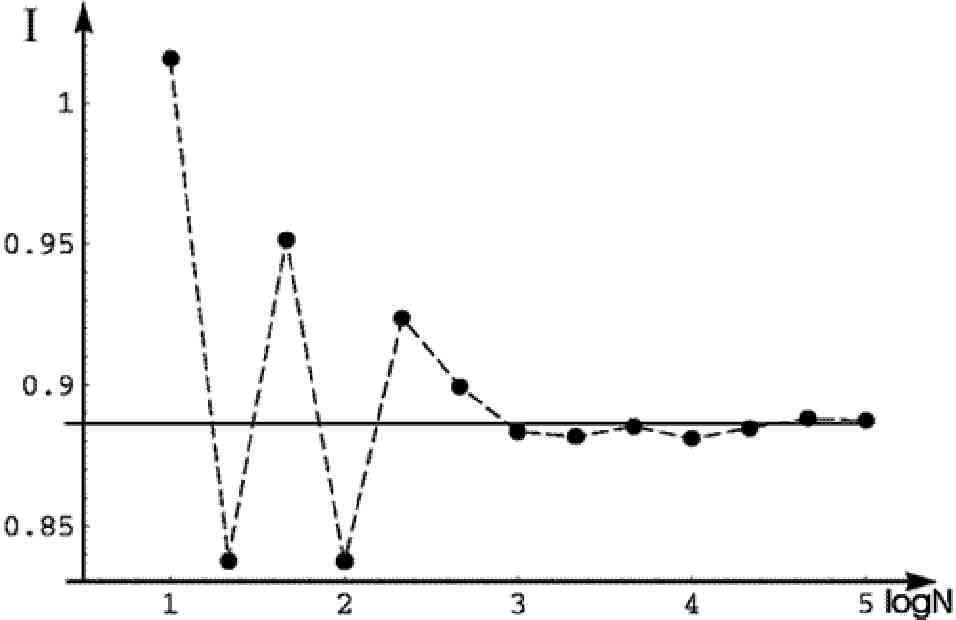
Рис. 15. Результаты вычисления интеграла модифицированным методом статистического моделирования.

4.2. Метод исключения

33

Из этого примера видно, что модифицированный метод можно исполь­зовать для вычисления несобственного интеграла с бесконечными преде­лами. Этого нельзя сделать рассмотренным ранее методом, где случайные точки были равномерно распределены в прямоугольнике, в который впи­сана подынтегральная функция.

4.2. Метод исключения

Метод функции распределения реально можно использовать лишь в том случае, если интеграл (16) и обратная функция F~^l(x) вычисляют­ся аналитически. В противном случае приходится использовать другие методы, одним из которых является метод исключения.

Пусть прямоугольник (Ь — а) х h заполняется случайными точками равномерно и ж–координаты тех из них, которые оказались под кривой v(x) > 0, называемой функцией сравнения , принимаются в качестве слу­чайных чисел (рис.16). Остальные точки отбрасываются. Плотность ве­роятности для принятых чисел х равна

_ N_in(x е Ах)

^W^ ~ N_m Ах '

где Ni_n - полное число точек под кривой, а Ni_n(x Е Ах) - число точек под кривой в интервале Ах. Последнее, в свою очередь, пропорционально величине площадки, опирающейся на Ах, которая при малом Ах равна v(x)Ax, поэтому

N_m{x GAx)^| v{x) Ах

и

Отсюда следует, что

N_m^^L v{x) dx.

w(x) = <*) ,

fb v(x)dx

то есть для получения случайных чисел x с плотностью w(x) в качестве функции сравнения v(x) следует брать функцию, совпадающую с w(x) с точностью до нормировочного множителя. Легко видеть, что метод мож­но использовать, если величины h и b - a конечны.

Эффективность метода исключения равна отношению площади под кривой v(x) к площади прямоугольника. Она будет велика, если v(x) близка к константе. Метод не может быть реализован, если функция w(x) не ограничена, а также если область, в которой распределены случайные

34

4. Неравномерно распределенные случайные числа

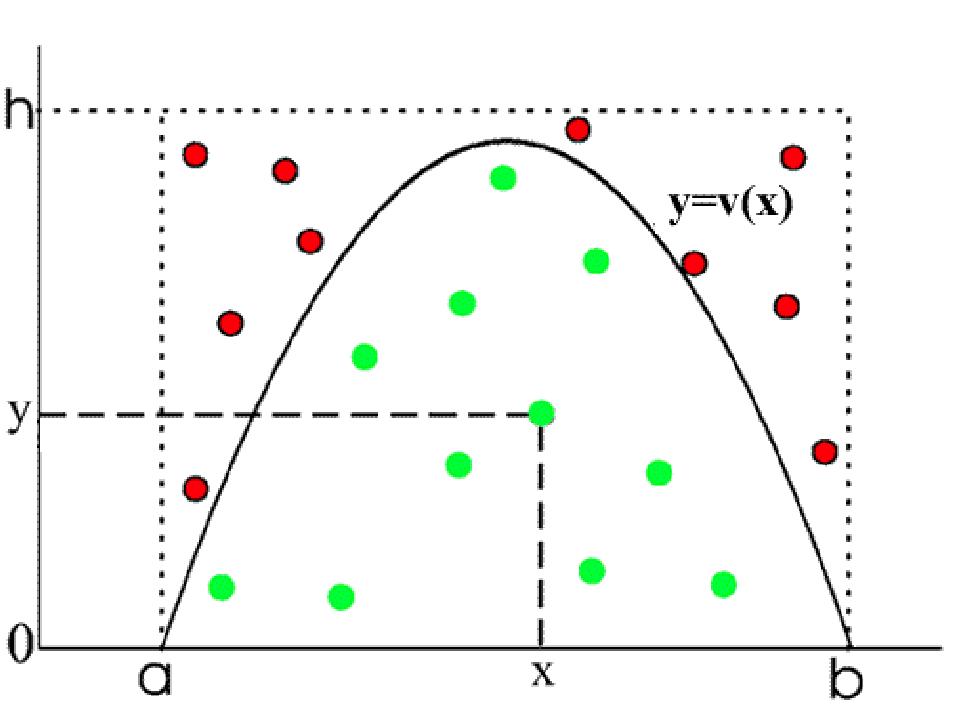
Рис. 16. Моделирование случайных чисел методом исключения.

числа x, бесконечна. В этих случаях или h, или (b - a) становятся беско­нечными.

Отметим, что описанный выше метод генерации случайных точек, рав­номерно распределенных в круге радиуса R, может служить примером, иллюстрирующим идею метода исключения.

Обобщение метода исключения. Если ж-координаты случайных

точек в прямоугольнике

выбирать на (a,b) не из равномерного

(b-a)xh

а (а, Ъ) не из ра распределения, как в предыдущем примере, а из распределения и(х), и использовать для отказов функцию v(x), разыгрывая у—координату, как и раньше, равномерно в (0, /г), то х– координаты оставшихся точек имеют плотность вероятности w(x), которая может быть найдена аналогично тому, как это сделано для метода исключения.

При моделировании ж—координаты из распределения и(х) в интервал Ах после N испытаний попадет Nu{x)Ax случайных точек, однако из них под кривой v(x) окажется и будет принято N и(х)Ах v(x)/h точек. Полное количество принятых точек равно интегралу от этого выражения

ь

(N/h) и(х) v(x) dx,

поэтому плотность вероятности равна

w(x)

u(x)v(x) ~ъ •

Ju(x)v(x)dx

Этот вариант метода исключения используется в тех случаях, когда плот­ность вероятности имеет вид произведения двух множителей.

4.2. Метод исключения

35

Пример такого моделирования для

w(x)

11

_TT^VI'

о <x < 1

представлен на рис.17. Моделирование величины x из распределения

u(x)

1

—— ₅

О < ж < 1

производилось методом функции распределения, а в качестве функции

сравнения использована функция v(x)

_гт^-

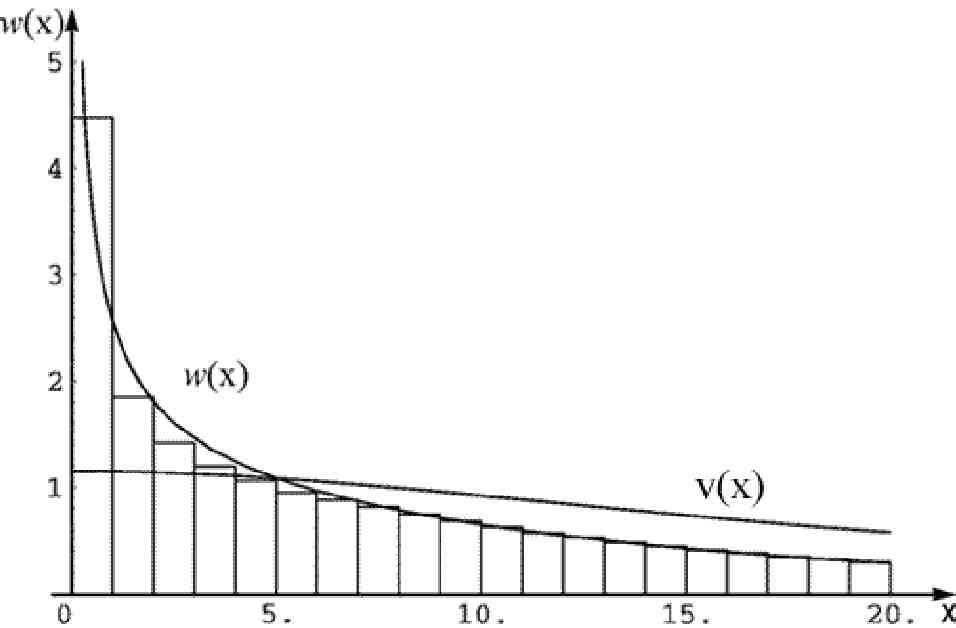
Рис. 17. Моделирование случайных чисел модифицированным методом исключения.

Из примера видно, что модифицированный метод исключения может быть использован и в том случае, если функция w(x) не ограничена. (В данном примере w(x) → ∞ при x → 0.)

Тождественное преобразование

Цж)

и(х)

позволяет моделировать распределение w(x), выбирая x из распределе-

ния u(x) и используя функцию

w(x)

в качестве функции сравнения. Для

w(x)

ф)

увеличения эффективности моделирования функцию u(x) следует выби-

было медленно меняющейся

рать таким образом, чтобы отношение

функцией, но выборку случайных чисел из распределения u(x) можно было провести методом функции распределения.

36

4. Неравномерно распределенные случайные числа

4.3. Метод суперпозиции

Пусть плотность вероятности случайных чисел х имеет вид суммы неотрицательных членов

w(x) = ^ u_k(x), «*(ж)>0, а<х<Ъ. (18)

к

Интегрируя обе части этого равенства по ж с учетом условия нормировки (1), получаем

У _j Ck = 1,

к где

ь

щ(х) dx.

Ск

Умножим и разделим на с_к каждый член суммы в (18) и запишем эту формулу в виде формулы полной вероятности (6):

w(x) = ^ c_kw_k(x), (19)

к

где

w_k(x) = щ(х)/с_к, ъ

w_k(x) dx = 1.

Отсюда следует, что алгоритм получения случайного числа x состоит в том, что числа c_k откладываются на отрезке (0,1), интерпретируются как вероятности и используются для определения ”номера дороги” k, а затем случайное число x разыгрывается из распределения w_k(x). Такой метод получения случайных чисел называется методом суперпозиции. Он легко обобщается на случай, когда ”номер дороги” в (19) пробегает непрерывный ряд значений и сумма заменяется интегралом:

w{x)= I с{к) w{x;k) dk.

4.4. Моделирование случайных точек в криволинейных координатах

Положение точки на плоскости можно задавать не только декарто­выми координатами х, у, но и полярными р, (р (рис.18).

4.4. Моделирование случайных точек в криволинейных координатах 37

Рис. 18. Полярные координаты.

Моделирование полярных координат случайных точек в некоторых случаях может оказаться предпочтительным. В качестве примера рас­смотрим обсуждавшуюся ранее задачу о моделировании точек, равномер­но распределенных в круге радиуса R.

Если в круге равномерно распределены N случайных точек, то их

средняя плотность равна ——г, количество точек на площадке ds равно

N(f<E ds) = ——г ds, а вероятность попадания в ds равна 7Г R^z

^ N(feds) ds

^p{r ^G ds) = N = VW'

Подставляя в эту формулу выражение для ds в полярных координатах

ds = dpdl = р dp dip,

видим, что вероятность P(f G ds) можно представить в форме

P(feds)=w_p(p)dpw_(p(if)dif,

где

_Wp(p) = |£, 0 < р < R

есть плотность вероятности для полярного радиуса р, а

_W(p(<p) = —, 0 < if < 2тг

есть плотность вероятности для азимута if.

Попадание случайной точки на площадку ds означает, что ее коор­дината р принадлежит интервалу dp, а координата ip - интервалу dip.

38

4. Неравномерно распределенные случайные числа

Поэтому вероятность P(f Е ds) оказалась равной произведению двух со­множителей, зависящих от р и р.

Случайные числа р и р с указанными распределениями могут быть по­лучены методом функции распределения из равномерно распределенных чисел 7 по формулам:

р = R л/т"? р = 2тт 7-

Случайные точки, равномерно распределенные на поверхно­сти сферы и в объеме шара. Если N случайных точек равномерно рас­пределены по поверхности сферы радиуса R, то их средняя плотность рав­на -—~2, количество точек на площадке ds равно N(f Е ds) = -——^ ds, а вероятность попадания в ds равна

^ N(feds) ds

^{Р{Г G} ds) = N = bT&'

Величина элементарной площадки ds, образованной близкими парал­лелями и меридианами, в сферических координатах равна

ds = R² sintfdtfdp,

поэтому

P(f е ds) = w${$)d$ w^{p)dp,

где

есть плотность вероятности для полярного угла #, а

_W(p(p) = —, 0 < р < 2тг

есть плотность вероятности для азимута р.

Здесь, как и в предыдущем примере, попадание случайной точки на площадку ds означает, что ее полярный угол # принадлежит интервалу dfi, а азимут р - интервалу dip. Поэтому вероятность P(f Е ds) равна произведению сомножителей, зависящих от углов # и р. Случайные числа $ и р с указанными распределениями легко могут быть получены методом функции распределения из равномерно распределенных 7 .

Равномерное распределение точек на сфере означает, что единичный вектор Q = г/г с проекциями

O^sintf cos (£,

4.4. Моделирование случайных точек в криволинейных координатах 39

£\ = sintf sinp, ft_z = costf

имеет изотропное распределение. Такое распределение имеют, например, направления вылета частиц при радиоактивном распаде, и эти формулы можно использовать для моделирования начального направления движе­ния частицы.

Аналогичные рассуждения для случайных точек, равномерно распре­деленных в объеме шара, дают

P(fe dV) = w_r(r)dr w<>(ti)d& w^dif,

где

_Wr[r) = ^L.^ Q<r<R,

_W(p(<p) = —, 0 < (f < 2тг

- плотности вероятности для сферических координат г, #, (/?, для моде­лирования которых также можно использовать метод функции распреде­ления.

В задачах теории переноса равномерное распределение могут иметь точки, где частицы рождаются в источнике. Их сферические координаты можно моделировать с помощью описанного метода.

Моделирование нормального (гауссовского) распределения.

Представим себе, что маленькие кусочки бумаги падают на пол с некото­рой высоты. Траектория и место падения каждого кусочка будут, очевид­но, случайными, однако форма ”горки”, образуемой ими на полу, облада­ет статистической устойчивостью. Плотности вероятности, описывающие распределения х и у - координат случайных точек в таких задачах, обыч­но считаются гауссовскими, и если начало координат находится в центре ”горки”, то

w_x(x) = _l=exp(-Aj), -оо < х < оо,

wJy) = —l=exp(-JL-), -оо < у < оо, о\р2ж 2а²

где а² - дисперсия - параметр, характеризующий ”ширину горки”.

40

4. Неравномерно распределенные случайные числа

Выделим на плоскости площадку ds = dx dy. Тогда вероятность того, что точка попадет в ds, равна

P(r е ds) = Р(х е dx) Р{у е dy) = -1_техр(-^Ж + 2^У ) dx dy. В полярных координатах х² + у² = р², ds = р dp dip, поэтому

P(f е ds) = -JL _ехр(-^)р dp dp.

Это значит, что плотности вероятности случайных величин р и р имеют вид

_Wp(p) = -L ехр(—^Р—) р, 0 < р< оо,

«v(<rf = ^-, 0 < р < 2тг. С такими плотностями вероятности метод функции распределения дает

V

p = <7-21og7,

V9 = 2тг7,

где числа 7 равномерно распределены в (0,1).

Если от полученных моделированием полярных координат р, р перей­ти к декартовым, то случайные величины

х = xq + р cosp,

у = у₀ + р _Sin р

будут иметь нормальное распределение со средними значениями жо, Уо и дисперсией а².

Результат моделирования нормального распределения представлен на рис.19.

Отметим, что нормальное распределение часто встречается при ре­шении научных и прикладных задач, где описанный метод может быть использован для моделирования.

Вопросы

41

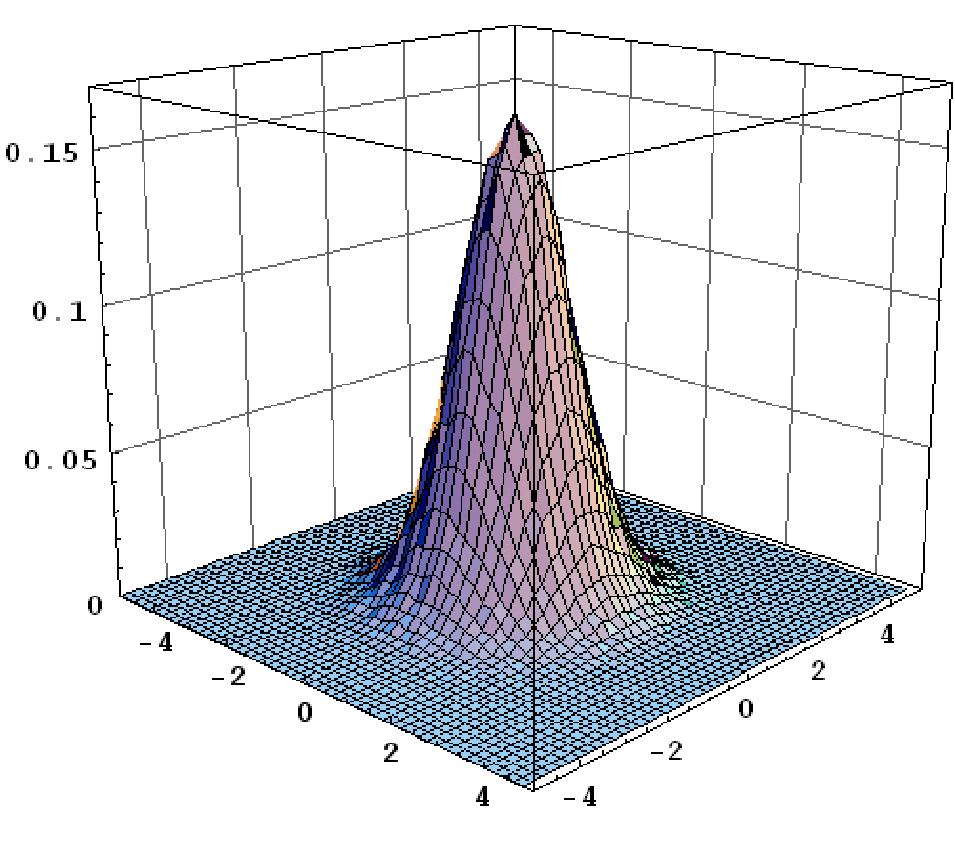
Рис. 19. Результаты моделирования двухмерного нормального распреде­ления.

Вопросы

56. Опишите алгоритм получения случайных чисел методом функции распределения. Объясните, в каких случаях он не может быть ис­пользован.

57. Опишите два способа вычисления определенных интегралов мето­дом Монте-Карло.

58. Опишите алгоритм получения случайных чисел методом исключе­ния.

59. Опишите способы увеличения эффективности метода исключения.

60. Опишите алгоритм получения случайных чисел методом суперпо­зиции.

61. Получите формулы, связывающие декартовы координаты с цилин­дрическими и сферическими. Запишите выражения для длины ду­ги, элемента поверхности и элемента объема в криволинейных ко­ординатах.

62. Опишите алгоритм получения случайных точек, равномерно рас­пределенных в круге, на поверхности сферы и в объеме шара с ис­пользованием криволинейных координат.

63. Опишите алгоритм получения случайных точек, распределенных на плоскости по нормальному закону.

42

4. Неравномерно распределенные случайные числа

Упражнения

1. Проверить нормировку и построить графики распределений w(x)

• mexp(—тх), (0 < х < оо) — экспоненциальное распределение,

• -^i, (1 < ж < оо)-распределение Парето,

• , 1 (-1<ж<1). ^8(1-ж) ~ ~

Исследовать, как меняется вид распределений с изменением пара­метров.

64. Составить блок-схему и подпрограмму моделирования случайных чисел методом функции распределения для плотностей вероятно­сти Упражнения 1. Привести результаты моделирования несколь­ких случайных чисел.

65. Проверить нормировку и построить график плотности вероятности

Цж) = 5(1-ж2 ), (-1<Ж<1).

Составить блок-схему и подпрограмму для генерации случайных чи­сел х методом исключения. Привести результаты моделирования нескольких случайных чисел.

4. Проверить нормировку и построить график плотности вероятности

оо

w(x) = [ с к~^с ехр(-хк) dk, (0<х< ос).

Исследовать, как меняется вид распределения с изменением пара­метра c. Получить моделирующие формулы, составить блок-схему и подпрограмму выборки случайных чисел из этого распределения методом суперпозиции, используя для вычисления ”номера дороги” k предэкспоненциальный множитель подынтегрального выражения. Привести результаты моделирования нескольких случайных чисел.

5. Получить моделирующие формулы, составить блок-схему и подпро­грамму для получения случайных точек, равномерно распределен­ных на поверхности сферы, используя сферические координаты. При­вести результаты моделирования координат нескольких случайных точек.

Задачи

43

Задачи

66. Составить программу моделирования случайных чисел методом функ­ции распределения для плотностей вероятности Упражнения 1. При­вести результаты моделирования распределений.

67. Составить программу для вычисления определенного интеграла

оо

/= fexp{-ax)sm{bx)dx 0

методом Монте-Карло, используя первый множитель подынтеграль­ного выражения для генерации случайных значений х. Сравнить результаты моделирования при различных N с точным значением I.

3. Составить программу для генерации случайных чисел х из распре­ деления

w(x) = -х2 ), (-1<ж<1)

методом исключения. Привести результаты моделирования распре­деления.

4. Составить программу для получения случайных чисел с плотностью вероятности

оо

w(x) = [ с к~^сехр(-хк) dk, (0 < х < ос) 1

методом суперпозиции, используя для вычисления ”номера дороги” к предэкспоненциальный множитель подынтегрального выражения. Привести результаты моделирования распределения.

5. Составить программу и провести моделирование распределения слу­ чайных чисел у, если

• у есть сумма двух случайных чисел х, распределенных с плот­ностью Цж),

• у есть разность двух случайных чисел х, распределенных с плотностью w(x),

• у есть меньшее из двух случайных чисел х, распределенных с плотностью w(x),

44

4. Неравномерно распределенные случайные числа

• y есть большее из двух случайных чисел x, распределенных с плотностью w(x).

В качестве w(x) использовать равномерное и экспоненциальное распределения.

6. Использовать программу C-DISTRIBUTION для получения случай­ных точек, распределенных на плоскости по нормальному закону.

Проблемы

1. Методы моделирования неравномерно распределенных случайных чисел.

5. Распределение Пуассона

5.1. Прохождение частиц через вещество

Пусть поток частиц с плотностью потока Фо 1/(см² сек) падает на поглотитель, состоящий из хаотически расположенных атомов с попереч­ником (7 см², а среднее количество атомов в единице объема равно щ 1/см³ (рис.20).

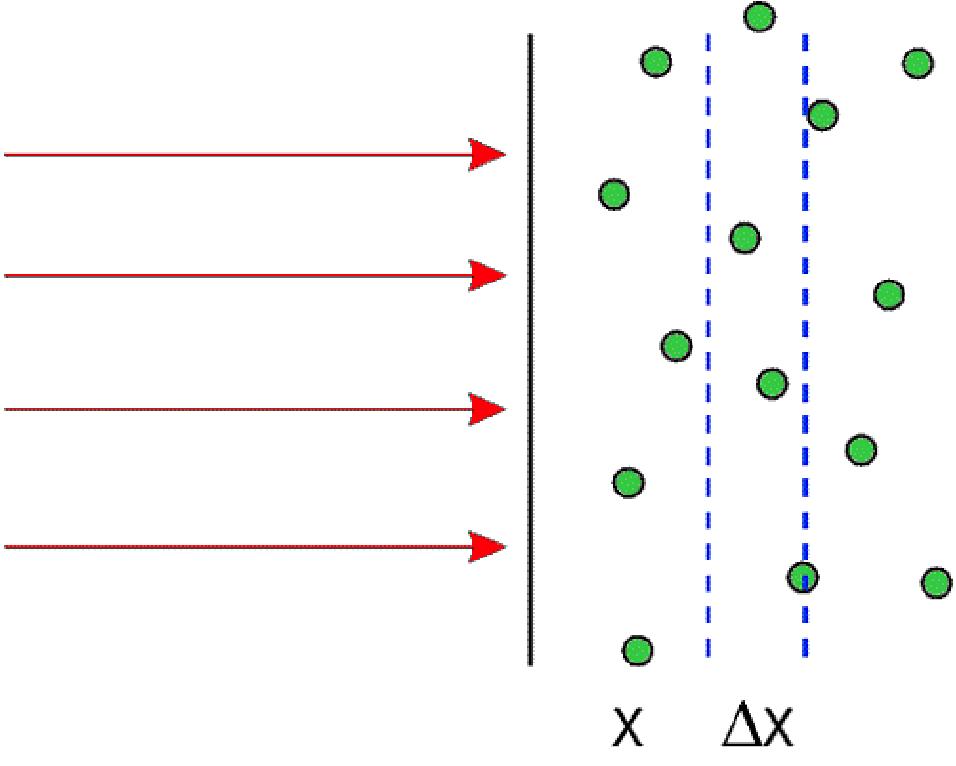
Рис. 20. Прохождение частиц через вещество.

Если при столкновении с атомами частицы поглощаются, то плот­ность потока Ф(х) будет случайной функцией глубины: после каждого столкновения количество частиц уменьшается на единицу и Ф(ж + Ах) = Ф(х) — Q(Ax), где Q(Ax) - количество частиц, поглощенных на квадрат­ном сантиметре в слое Ах в единицу времени. Очевидно, что это равен­ство остается справедливым и после усреднения по многим эксперимен-

там:

Ф(х + Ах) = Ф(х) - Q(Ax

(20)

Легко видеть, что среднее количество столкновений потока частиц Ф(х) с одним атомом в единицу времени равно аФ(х), а щАх есть коли­чество атомов на 1 см ² в слое Ах, поэтому Q(Ax) равно их произведению:

Q(Ax) = Ф(х) ащ Ах.

(21)

Отношение среднего числа столкновений в слое Ах к среднему числу частиц, падающих на этот слой,

Q(Ax) Ф(х)

fiAx

46

5. Распределение Пуассона

есть среднее количество столкновений на пути Ах, приходящихся на одну частицу, а /i = ащ - среднее число столкновений на единице пути.

Подставляя (21) в (20) и переходя к пределу Ах ->• 0, получим диф­ференциальное уравнение для Ф(х) :

(1Ф -

dx ^f '

Его решением, удовлетворяющим очевидному граничному условию Ф(0) = Ф₀, является функция

Ф(х) = Ф₀е^^х. (22)

Из (22) видно, что 1/ц численно равно глубине, на которой средняя плотность потока Ф убывает в е раз, поэтому величина /i называется линейным коэффициентом ослабления.

Отношение среднего числа частиц, которые прошли путь х без взаи­модействия, к числу частиц, падающих на поглотитель,

Р₀(_ж) = ^М. = _е-и*

есть вероятность пройти этот путь без взаимодействия.

Пусть теперь частицы в веществе не только поглощаются, но и рассеи­ваются, то есть меняют направление движения при столкновениях. В этом случае путь частицы представляет собой ломаную линию, состоящую из звеньев случайной длины. Обозначим через х длину пути, пройденного частицей вдоль траектории, мысленно вытянув траекторию в прямую ли­нию. На этом пути частица испытывает случайное количество столкнове­ний, поэтому среднее число частиц, прошедших путь х, можно записать в виде суммы

ф(_ж) = ф₀(_ж) + ф^х) + Ф₂(х) + ...,

где Фк(х) - среднее количество частиц, испытавших к столкновений на пути х. Разделив обе части этого равенства на Ф(х), получим условие нормировки

оо

к=0 Фи(х)

где Р_к(х) = - ; / - вероятность испытать к столкновений. Ф(х)

Легко видеть, что, как и раньше, Pq{x) = е~^мж, а для малого пути Ах, когда можно пренебречь возможностью испытать более одного столкно­вения, с учетом (21) получается, что

P_l(Ax) = fiAx,

5.2. Радиоактивный распад

47

то есть /i есть вероятность столкновения на единице пути. Вид вероят­ностей Р_к(х) для произвольных ки х обсуждается ниже.

Путь ж, пройденный частицей в веществе до первого столкновения, случаен, и вероятность того, что это столкновение произойдет в интерва­ле (ж,ж + Ах), можно найти, если учесть, что для частицы, вылетевшей из начала координат, первое столкновение в интервале (ж, х + Ах) можно считать композицией двух случайных событий: ”отсутствие взаимодей­ствий на пути ж” (вероятность этого события равна е~^^х) и ”столкновение в Аж” (соответствующая вероятность равна цАх). Поэтому Р(х G Ах) равно произведению двух указанных сомножителей:

Р(х е Ах) = е'^цАх.

Плотность вероятности того, что столкновение произошло в точке х, найдем по формуле (3)

w(x) = ц е""*, 0 < х < оо. (23)

Функция w(x) описывает распределение частиц по пробегам.

Генерируя случайные числа х из распределения (23), мы моделируем длину пробега частицы. Их можно использовать для вычисления средней длины пробега частицы:

, i^

< I > = — > Xi.

N ^ i=i

В соответствии с (17) такое среднее можно записать в виде интеграла

оо

/ х /j, е~^^х dx, который равен l//i, следовательно, величина 1//J, есть o средний пробег частицы до столкновения.

5.2. Радиоактивный распад

Пусть мы имеем Щ радиоактивных атомов. Время жизни каждого из них случайно, поэтому количество нераспавшихся атомов N(t) является случайной функцией времени: после каждого распада количество атомов уменьшается на единицу. Как и в задаче о поглощении частиц, для сред­него по многим экспериментам справедливо равенство

N(t + At) = N{t)-Q{At),

где Q(At) - среднее количество атомов, распавшихся за время At. Оно пропорционально количеству нераспавшихся атомов в момент t и вели­чине промежутка At:

Q(At) = fiAtN(t),

48

5. Распределение Пуассона

поэтому, как и в предыдущем примере,

dN

-fiN,

dt

N(t) = Noe-*.

Величина /i называется постоянной распада. Ее физический смысл анало­гичен тому, что говорилось в предыдущем примере: /j, - это среднее число распадов в единицу времени и вероятность распада в единицу времени, а l//i- время, за которое количество атомов уменьшается в е раз, и среднее время жизни атома.

Момент распада атома можно изобразить точкой на временной оси, и попадание точки в интервал (t,t + At) считать композицией двух слу­чайных событий: ”выживание атома за время (0,*)” (вероятность этого

события равна ^ = е""*) и ”распад за время АГ (соответствующая

вероятность равна fiAt). Поэтому если атом существовал при t = 0, то вероятность распада в момент t Е At равна произведению двух указан­ных вероятностей:

P(t Е At) = е-* fiAt,

а плотность вероятности распада в момент t равна

w(t) = /le-*.

Моделируя t из этого распределения, можно находить случайное время жизни атома.

В системе, состоящей из нескольких радиоактивных атомов, случай­ным является момент первого распада, и вероятность того, что этот рас­пад произойдет в интервале (t,t + At), можно найти как композицию вероятностей двух случайных событий: ”выживание всех атомов в интер­вале (0, t)” и ”распад одного из атомов за время At”. Если в начальный момент имелось N радиоактивных атомов, то (е~^и1)^м есть вероятность того, что к моменту t все они выжили (не распались и первый, и второй, ...и N-й атомы), а NfiAt - вероятность того, что за At распадется один из них (или первый, или второй, ... или N-й). Поэтому

_WN(t) = fiN e~^^Nt

есть плотность вероятности для моделирования момента первого распада в системе, состоящей из N атомов. Уменьшая N после каждого распада на единицу, можно моделировать случайное N(t).

Результат моделирования радиоактивного распада представлен на рис.21.

5.3. Многоканальный и сложный радиоактивный распад 49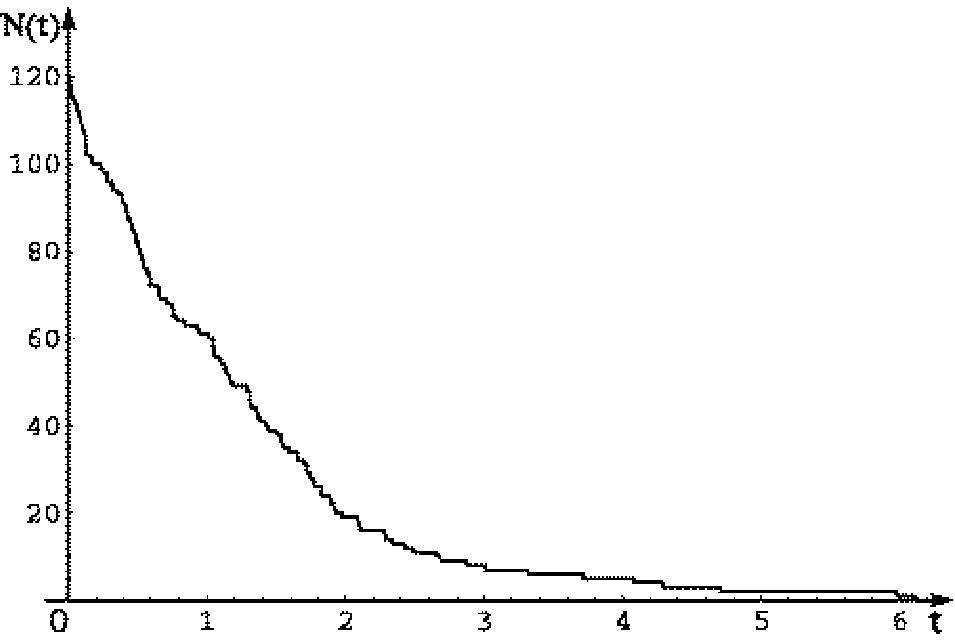

Рис. 21. Результат моделирования кривой радиоактивного распада.

При больших значениях N статистическим характером процесса рас­пада можно пренебречь и считать, что количество радиоактивных атомов убывает по экспоненциальному закону. При малых N экспоненциальный закон справедлив только для среднего по большому количеству экспери­ментов.

Распад радиоактивных ядер приводит к образованию дочерних ядер - продуктов распада, и их накопление может автоматически подсчиты-ваться при моделировании.

5.3. Многоканальный и сложный радиоактивный распад

Для атомов с несколькими способами (каналами) распада постоянная распада /i равна сумме парциальных постоянных /i^, соответствующих различным каналам:

/i = 2.1М)

г

и Pi = fii/fi есть вероятность распада по i-му каналу. Зная эти вероятно­сти, тип распада можно находить моделированием. Для этого вероятно­сти Pi надо отложить на отрезке (0,1) и по равномерно распределенному случайному числу 7 определять номер канала. Совместное моделирова­ние случайной функции N(t) и типа распада является моделированием такого распада и накопления его продуктов.

Если какие-то продукты распада сами радиоактивны (сложный ра­диоактивный распад), то момент распада очередного дочернего ядра мо­делируется по той же схеме с учетом того, сколько ядер данного элемента существовало до этого распада. В этом случае динамика процесса носит более сложный характер, так как некоторые ядра могут не только распа­даться, но рождаться в результате предыдущих распадов.

50

5. Распределение Пуассона

Сам расчет сложного радиоактивного распада проводится следующим образом. Составляется список всех веществ, которые могут образоваться на разных этапах распада, и задается начальное количество каждого из этих элементов. Для каждого из них по описанной выше схеме вычисля­ется момент первого распада. Они сравниваются между собой для того, чтобы определить, какой именно распад произойдет первым. Количество атомов распавшегося элемента уменьшается на единицу, а количество со­ответствующих дочерних атомов на единицу увеличивается. После этого процесс моделирования повторяется. Расчет ведется до тех пор, пока в системе есть радиоактивные атомы.

5.4. Моделирование процесса размножения-гибели

В задачах биологии и медицины организмы не только умирают но и рождаются. Пусть fiAt есть вероятность гибели за время At, а и At - вероятность рождения за то же время. Тогда (/i + и)At - вероятность

рождения или гибели за At. Обозначим Е = /i + v, тогда отношения —

и — определят относительные вероятности гибели и рождения. Последо­вательное моделирование момента времени, когда происходит изменение количества организмов в системе, и типа процесса (рождение или гибель) позволяет моделировать процесс эволюции популяции. В тех случаях, ко­гда у одного организма возможно рождение нескольких близнецов, алго­ритм моделирования дополняется розыгрышем количества потомков по известным вероятностям иметь к потомков, как это делалось в разделе 2. Результат моделирования эволюции популяции при различных соот­ношениях между вероятностями рождения и гибели организмов представ­лен на рис.22.

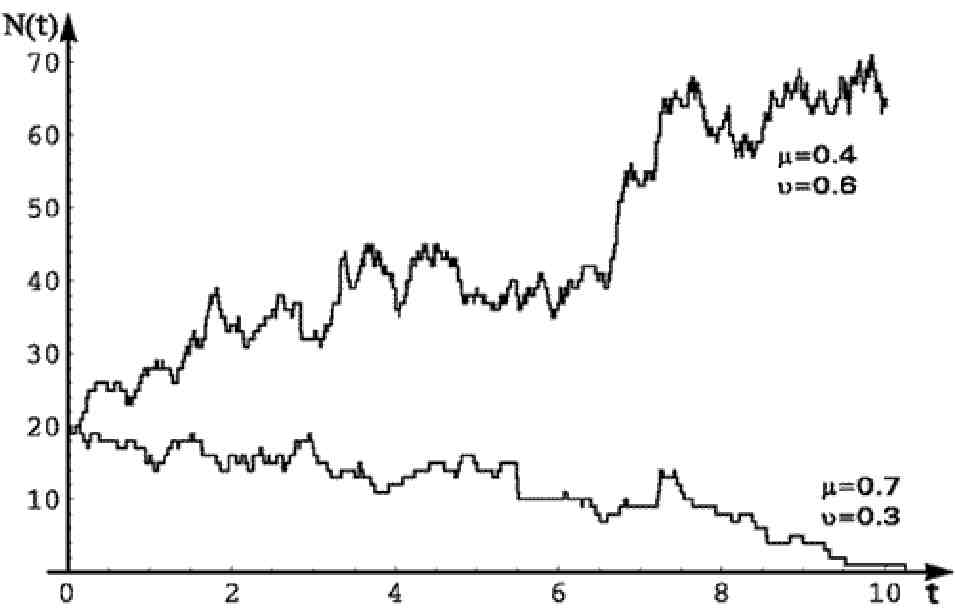
Рис. 22. Результаты моделирования эволюции популяции во времени.

Из рисунка видно, что при /j, < v численность популяции в среднем растет, а при /j, > v - уменьшается.

5.5. Распределение Пуассона

51

Аналогичные задачи типичны для физики космических лучей, где приходится рассматривать каскады высокоэнергетических частиц, каж­дая из которых при взаимодействии с атомом вещества может поглотить­ся или родить случайное количество вторичных частиц.

5.5. Распределение Пуассона

Пусть капли дождя падают на выделенный участок дороги (или ча­стицы космических лучей падают на детектор) в случайные моменты вре­мени t_ht₂,.... Количество капель, упавших за время At, случайно, оно может быть равно 0,1, 2,..., и для соответствующих вероятностей можно записать условие нормировки:

оо к=0

Так же, как и в задачах о поглощении частиц в веществе или радиоак­тивном распаде, будем считать, что при малом At вероятность Pi(At) пропорциональна At :

P_l{At) = vAt, (24)

а Р2,-Рз, ••• имеют более высокий порядок малости, и ими в условии нор­мировки можно пренебречь. В этом приближении

P₀{At) = 1 - vAt. (25)

Для того чтобы найти вероятность Ро для временного интервала ко­нечной длительности, будем считать отсутствие капель в интервале (0, t + At) композицией двух случайных событий: ”отсутствие капель в (О,*)” и ”отсутствие капель в At .” Тогда

P_{){t + At) = P_{){t) P₀{At).

Подставляя в эту формулу выражение (25) для P₀(At) и переходя к пре­делу At —>■ 0, получим формулу, аналогичную тем, что были получены в задачах о прохождении частиц через вещество и радиоактивном распаде:

"^v ' + vP₀{t) = 0.

Из (25) следует, что Ро(0) = 1, поэтому

Po(t) = e~^vt.

52

5. Распределение Пуассона

Величина v называется интенсивностью потока и равна среднему числу капель, падающих в единицу времени.

Промежуток времени между двумя каплями случайный и по аналогии с выше рассмотренными примерами вероятность того, что его длитель­ность будет лежать в интервале (t, t + At), равна

Pit е At) = e7^vt vAt,

плотность вероятности, которую можно использовать для моделирования величины промежутка времени между каплями, имеет вид

w(t) = ve-",

а среднее значение промежутка времени между двумя каплями равно 1/v. Для того чтобы найти вероятность Р\ для конечного временного ин­тервала, отметим, что падение одной капли за время (0,£ + At) означает, что ”одна капля упала за время (0, t) и нет капель за At” или ”нет капель за время (0, t) и одна капля упала за At.” Поэтому

Piit + At) = P_x{t) P₀{At) + P₀{t) Pi{At).

Используя формулы (25), (24) для P₀(At) и Pi(At) и переходя к пределу Д£ ->■ 0, получим неоднородное дифференциальное уравнение

⁽M^l + _vp_l(t) = vP₍₎{t).

Начальное условие для функции P^t) в соответствии с (24) имеет вид Pi(0) = 0.

Аналогичным образом можно показать, что при к > О

Щ^1 + _vP_k{t) = vPk.^t),

Pk{0) = 0.

Подстановка

P_k{t) = e'^Pkit) приводит это уравнение к виду

= V' Ph 1 ( t ) ,

dt

Р_Л(0) = 0.

Вопросы

53

Последовательное интегрирование этого уравнения при к = 1,2,.. с уче-том того, что Po(t) = 1, дает Pk(t) = ———, откуда следует, что

т = &£*■*. (26)

Полученное решение называется распределением Пуассона. Легко прове­рить, что вероятности Puit) удовлетворяют условию нормировки:

оо

j2Pk{t) = i,

к=0

поэтому, отложив числа Pk на отрезке (0,1), по равномерно распределен­ному случайному числу 7 можно моделировать случайное число к.

Цепочка случайных событий с экспоненциальным распределением вре­менных интервалов между ними или со случайным к и вероятностями Pk, которые определяются формулой (26), называется пуассоновским пото­ком событий.

Установлено, что распределение Пуассона описывает количество про­данного товара, пойманных рыб, забастовок или войн, опечаток в тексте, звонков на телефонной станции, травм на производстве, распавшихся ра­диоактивных ядер или вышедших из строя тракторов. После замены вре­мени t на пройденный путь оно описывает количество проколов колеса или количество столкновений частицы в веществе. А после замены (наг его используют при анализе числа частиц, упавших на одинаковые пло­щадки AS, испытавших взаимодействия в одинаковых объемах AV, и т.д. Все эти процессы могут быть исследованы методами статистического мо­делирования.

Вопросы

68. Опишите основные величины, характеризующие ослабление потока частиц в веществе: среднее количество частиц, поглощенных в слое Ах, закон ослабления, средняя длина свободного пробега.

69. Опишите физический смысл коэффициента /i в задаче о прохожде­нии частиц через вещество.

70. Частицы стартуют из начала координат. Какой вид имеет вероят­ность столкновения в интервале (х, х + Ах) и плотность вероятно­сти для пробегов? Опишите физический смысл сомножителей этой функции. Как моделировать длину пробега частицы в веществе?

54

5. Распределение Пуассона

71. Опишите основные величины, характеризующие процесс радиоак­тивного распада: среднее количество атомов, распавшихся за время At, закон распада, период полураспада и среднее время жизни ра­диоактивного атома.

72. Опишите физический смысл постоянной распада.

73. Какой вид имеет плотность вероятности распада в момент t? Опи­шите физический смысл сомножителей этой функции. Как модели­ровать время жизни радиоактивного атома?

74. Какой вид имеет плотность вероятности для момента первого рас­пада в системе из N атомов? Опишите физический смысл сомно­жителей этой функции. Как моделировать изменение количества радиоактивных атомов во времени?

75. Как моделировать изменение количества радиоактивных атомов и продуктов распада во времени, если атомы распадаются по несколь­ким каналам? Как моделируется сложный радиоактивный распад?

76. Перечислите вероятностные характеристики процесса размножения и гибели живых организмов и опишите способ моделирования этого процесса.

77. Опишите вероятностные характеристики пуассоновского потока со­бытий для малого интервала At.

78. Как выводятся дифференциальные уравнения для вероятностей

79. Какой вид имеет плотность вероятности для промежутка времени между событиями в пуассоновском потоке?

80. Приведите примеры задач, где можно пользоваться распределением Пуассона.

Упражнения

81. Вывести и решить дифференциальные уравнения для распределе­ния Пуассона. Проверить нормировку распределения.

82. Составить таблицы и построить графики распределения Пуассона при нескольких значениях параметра т = vt. Исследовать зависи­мость вида распределения от параметра т = vt.

Задачи

55

83. Используя формулу (26), вычислить Р₀, получить рекуррентную формулу (10), составить блок-схему и подпрограмму моделирова­ния номера интервала к, в который попадает равномерно распре­деленное в интервале (0,1) число 7, для распределения Пуассона. Использовать подпрограмму для получения нескольких значений к.

84. Составить блок-схему и подпрограмму моделирования времени жиз­ни радиоактивного ядра. Использовать ее для получения несколь­ких значений t.

Задачи

85. Составить программу для моделирования времени жизни радиоак­тивного ядра. Привести результаты моделирования соответствую­щей плотности вероятности w{t).

86. Составить программу для вычисления времени Т, за которое рас­падутся N_t радиоактивных ядер. Получить несколько значений Т.

87. Составить программу для вычисления среднего времени, за которое распадутся N_t радиоактивных ядер. Исследовать зависимость этой величины от N_t.

88. То же для периода полураспада.

89. Составить программу для моделирования момента распада каждого из N_t радиоактивных атомов. Использовать эти данные для постро­ения случайной кривой N(t).

Указание. Создать массив Т = {0,£_ь*2, •••%}, где t_k - момент распада к-го атома, и преобразовать его в случайную кривую N(t) командами

« Graphics¹ Graphics¹

Т_р = Table[{l/2{T[[k]]+T[[k+l}}), N_t+l-k,T[[k+l]}-T[[k}}}, {к, N_t}}-

GeneralizedBarChart[T_p].

Исследовать изменение характера случайной функции N(t), опреде­ляющей количество нераспавшихся ядер, при увеличении начально­го количества ядер.

6. Количество бактерий в популяции N{t) является случайной функ­ цией. Ее вид определяется интенсивностями рождения и гибели, ко­ торые равны v и /i, соответственно. Провести моделирование N(t) (N(0) = N_t, 0 < t < Т) при [i>v, jJL = v, [i<v.

56

5. Распределение Пуассона

Проблемы

90. Прохождение частиц через вещество, радиоактивный распад, про­цесс размножения-гибели.

91. Распределение Пуассона.

6. Основные понятия теории переноса частиц

Сложный процесс прохождения частиц через вещество в большинстве случаев можно представить в виде последовательности элементарных эта­пов: испускание частицы источником, одно или несколько взаимодействий с атомами, в промежутках между которыми частица движется свободно, и, наконец, поглощение или вылет из рассматриваемой системы. Ниже пе­речислены основные понятия, которые используются для описания каж­дого из этих этапов.

6.1. Плотность распределения источников

Состояние частицы в определенный момент времени t будем описы­вать набором переменных f,Q,E, представляющих собой радиус-вектор точки, где находится частица, направление ее движения и энергию, соот­ветственно. Совокупность этих переменных будем обозначать буквой г и называть фазовыми координатами. Множество их значений называется фазовым пространством, а произведение At = AV AQ АЕ - элемен­тарным фазовым объемом.

Количество частиц, испускаемых реальными источниками, и их на­чальные фазовые координаты обычно являются случайными. Их распре­деление описывается функцией S(f, Q, Е, t), которая равна среднему чис­лу частиц, испускаемых в единицу времени единичным фазовым объемом около точки (г, Q, Е):

N(t g Ar, At)

S(f,Q,E,t)= lim

Дт->о,д*->о At At

где N(t G Ar, At) - среднее количество частиц с энергией Е G АЕ и направлением движения Q G AQ, испущенных в объеме AV за время At. Она называется дифференциальной плотностью источников.

Если функция S(f,Q, E,t) не зависит от t, f или Q, то источник на­зывается стационарным, однородным или изотропным, соответственно. Если зависимость этой функции от своих аргументов f,Q,E,t описыва­ется соответствующей (^-функцией:

S(r,U,E,t) = S _r (U,E,t) S(r-r ₀ ),

Syr,\l, Е,t) = Sq[t, E ,t) o[i} — "o) ?

S{f, U, E, t) = S_E{f, U, t) 6{E - E₀),

S(f, П, E, t) = S_t(f, П, E) 5(t - to),

58

6. Основные понятия теории переноса частиц

то источник называется точечным, мононаправленным, моноэнергети­ческим, мгновенным. Источник, обладающий всеми этими свойствами одновременно:

S(f, й, Е, t) = S_s 8{f- f₀) 8(U - й₀) 8(Е - Е₀) 8{t - to),

называется 8 -источником.

При решении задач переноса плотность распределения источников считается известной.

6.2. Полное и дифференциальное сечения взаимодействия

Пусть поток частиц с плотностью потока Фо 1/(см² сек) падает на атом. Будем считать, что силы, действующие между частицей и атомом, быстро убывают с расстоянием и столкновение испытают только те ча­стицы, у которых прицельный параметр меньше радиуса действия сил. Среднее количество столкновений Q в единицу времени пропорциональ­но плотности потока: Q = а Фо, где коэффициент пропорциональности

называется сечением взаимодействия. Для наглядности эту величину можно представлять как площадь круга, радиус которого равен радиусу действия сил. Однако при этом следует помнить, что в задачах атомной и ядерной физики радиус действия сил и сечение взаимодействия зави­сят не только от атома-мишени, но и от типа налетающей частицы и ее энергии.

Если при столкновении с атомом частица может поглощаться и рас­сеиваться, то количество столкновений Q представляется в виде суммы

Q = Q_c + Q_S} (28)

где Q_c и Q_s - количество поглощений и рассеяний в единицу времени, соответственно. Из формул (27) и (28) видно, что сечение взаимодействия о" можно записать как сумму

a(E) = a_c(E)+a_s(E),

где

а_с(Е) = ^

6.2. Полное и дифференциальное сечения взаимодействия 59

- сечение поглощения, а

а_а(Е) = ^

- сечение рассеяния.

Если кроме поглощения и рассеяния возможны другие типы взаимо­действия, например, деление, то сечением взаимодействия типа г называ­ется отношение

а_г(Е) = Q-,

где Qj— количество взаимодействий типа г в единицу времени.

В процессах рассеяния энергия частицы обычно меняется: Е —>■ Е', (Е'_тт < Е' < Е'_тах), и, разделив область изменения переменной Е' на интервалы АЕ', количество рассеянных частиц Q_s можно записать в виде суммы по интервалам:

q_s = J2Q_s(E' е АЦ), (29)

г

где Q_S{E' G АЕ[)- количество рассеяний с Е' е АЕ[.

Разделив обе части равенства (29) на плотность потока Фо, получим:

o-_s(E) = J2-fQs(E' £ АЕ[).

г

Преобразование

0-JE) = ^QJE' G АЩ) ^Ц ^v ^ Фо АЕ\

и переход к пределу АЕ[ —>■ 0 дают

_m

dE',

<r*{E)=

da_s(E';E) dW^f

Em^′ in

где

da_s(E';E) ₁ 1 Q_a(E' G AE')

dE' = a^o T₀ АЁ> (30)

-дифференциальное по E' сечение рассеяния, которое характеризует рас­пределение рассеянных частиц по энергии.

Разность q = Е — Е' представляет собой энергию, потерянную ча­стицей при столкновении, и по аналогии с (29), где рассеянные частицы сортировались по величине Е', их можно рассортировать по величине q.

60

6. Основные понятия теории переноса частиц

Распределение частиц по величине потерянной энергии характеризуется дифференциальным сечением

da_a(q\E) _ 1 Q_s{q G Aq)

dq ~ Aq^o Ф Aq '

где Q_s(g G Aq) - количество рассеяний с потерей энергии q G Aq.

При рассеянии частицы меняется не только ее энергия, но и направ­ление движения Q: Q —>■ Q', и по аналогии с (29) количество рассеянных частиц Q_s можно записать в виде суммы

q_s = J2Q_s(U' е AQ'i), (32)

г

где Qs($l' £ Л^) - количество частиц, рассеянных в телесный угол АО!_{. Это позволяет легко получить формулу:

а_а(Е)= jd^(T^'^E) d_n^

где

Щ*ЬЗ. = lim I Q.We*tt) (33)

- дифференциальное по Q' сечение рассеяния, характеризующее угловое распределение рассеянных частиц. В большинстве случаев оно зависит от полярного угла в между векторами Q и Q' и энергии налетающей частицы.

6.3. Макроскопические коэффициенты взаимодействия

Если поток частиц Фо падает на ”тонкую” мишень, состоящую из Щ не экранирующих друг друга атомов, заполняющих объем AV, то среднее количество столкновений в мишени в единицу времени будет равно

Q(AV) = N₀ (т(Е)Фо = щ а(Е) Ф₀ AV,

где щ = Nq/AV - плотность атомов. Величина

£(Я) = щ а(Е) (34)

называется макроскопическим сечением взаимодействия. В задачах пе­реноса гамма-излучения ее чаще называют коэффициентом ослабления. В п.5.1 было показано, что она представляет собой среднее количество столкновений на единице пути частицы в веществе.

6.4. Основные характеристики радиационных полей

61

Среднее количество поглощений и рассеяний на единице пути опреде­ляется формулами

Е_с(Я)=тю<7_с(Я),

Т,_а(Е)=ща_а(Е).

По аналогии с (34) величины

^{ЧЕ,Е)^Щ<Щ^1,}

dE>

называются макроскопическими дифференциальными сечениями. Они рав­ны количеству столкновений на единице пути с изменением энергии Е —>■ Е', с потерей энергии q и изменением направления движения Q —>■ ГУ, соответственно.

Учитывая физический смысл макроскопического дифференциального сечения T,(q;E), легко понять, что величина

(3(E) = qZ(q;E)dq (35)

есть средняя энергия, теряемая частицей на единице пути в веществе (тормозная способность вещества).

6.4. Основные характеристики радиационных полей

Источники излучения обычно испускают огромное количество ча­стиц, и целью экспериментального и теоретического исследования явля­ется определение некоторых средних характеристик потока этих частиц. Дифференциальная плотность частиц. В различных разделах физики и химии широко используется понятие плотность частиц, ко­торая в нестационарном случае определяется как среднее число частиц, находящихся в единичном объеме около точки г в момент t :

n(f,t) = lim

N(fe AV,t)

ду^о AV

где N(f E AV, t) - среднее количество частиц, находящихся в объеме AV в момент времени t. В теории переноса, где важным является то,

62

6. Основные понятия теории переноса частиц

что в момент t частицы могут иметь различные энергии Е и направления движения ft, обобщением понятия плотности является дифференциальная по Е и ft плотность частиц:

пУД^НПш^^ (36)

где N(r Е Ar, t) - среднее количество частиц в элементарном фазовом объеме Аг, то есть частиц с энергией Е Е АЕ и направлением движе­ния ft Е Aft, находящихся в момент времени t в объеме AV. Поэтому n(f, ft, Е, t) есть плотность частиц в фазовом пространстве.

Если распределение источников излучения и свойства среды не зави­сят от t, то и дифференциальная плотность частиц не будет зависеть от времени. Такие задачи называются стационарными.

Дифференциальная плотность потока частиц. С дифференци­альной плотностью частиц тесно связано понятие дифференциальной по ft и Е (или дважды дифференциальной) плотности потока частиц Ф(г, ft, E,t), которая определяется как

Ф(г, ft, Е, t) = v(E) n(f, ft, E, t), (37)

где v{E) - скорость частицы, имеющей энергию Е.

Если учесть, что v - это путь, который проходит частица в единицу времени, а n(f, ft, E,t) - количество частиц в единичном фазовом объеме около точки (г, ft, Е) в момент времени t, то Ф(г, ft, Е, t) - это путь частиц из единичного фазового объема в единицу времени.

Рассмотрим элементарную площадку As, с центром в точке г и нор­малью п. Из рис.23 видно, что за время At эту площадку пересекают только те частицы с энергией Е и направлением движения ft, которые находятся внутри параллелепипеда с основанием As и боковым ребром v At, направленным по ft. Объем этого параллелепипеда равен произве-

Рис. 23. Пересечение частицей площадки As.

6.4. Основные характеристики радиационных полей

63

дению площади основания на высоту:

AV = Asv At \(ttn)\,

а количество находящихся в нем частиц ”сорта tt, £” равно произве­дению дифференциальной плотности частиц на величину этого объема: n(f,tt,E,t) AV. Поэтому количество частиц с энергией Е е АЕ и на­правлением движения tt G Att, пересекающих площадку As за время At, равно

N{tt eAtt,EeAE, As, At) = <&{f,U,E,t)\{tt ft)\ Att AE As At, (38)

а дифференциальная плотность потока Ф(г, tt, Е, t) связана с числом пе­ресечений соотношением

^ N{Ue Att,Ее AE,As,At)

' ' ~~ ап^оае-$А8^о,аь^о \(tt п)\ Att AE As At

То есть Ф(г, tt, E,t) есть количество частиц с энергиями из единичного интервала около Е и направлением движения из единичного телесного угла около tt, пересекающих в единицу времени единичную площадку, перпендикулярную вектору tt.

В стационарных задачах, которыми мы в дальнейшем и ограничимся, дифференциальная плотность потока не зависит от времени.

Плотность потока частиц и плотность потока энергии. Радиа­ционное воздействие на вещество, находящееся в некотором объеме V, за­висит от того, сколько частиц падает на этот объем. Их количество можно выразить через определенную выше дифференциальную плотность пото­ка частиц. Для примера вычислим количество частиц, падающих в еди­ницу времени на поверхность сферы радиуса R, которую будем считать детектором (счетчик падающих частиц) (рис.24). Для этого мысленно разделим поверхность сферы на элементарные площадки ds и воспользу­емся приведенным выше выражением (38) для числа частиц, падающих на малую площадку в единицу времени. Суммирование (интегрирование) по всем площадкам, а также направлениям движения tt и энергиям Е частиц дает

I_N(t)= fdttfdE f ds\(ttn)\<£(f,tt,E,t). (39)

(Шг)<0

Условие (ttn) < 0 показывает, что для каждого направления tt интеграл по пространственным координатам берется по той части поверхности сфе­ры, для которой эти частицы являются входящими, то есть оно выделяет

64

6. Основные понятия теории переноса частиц

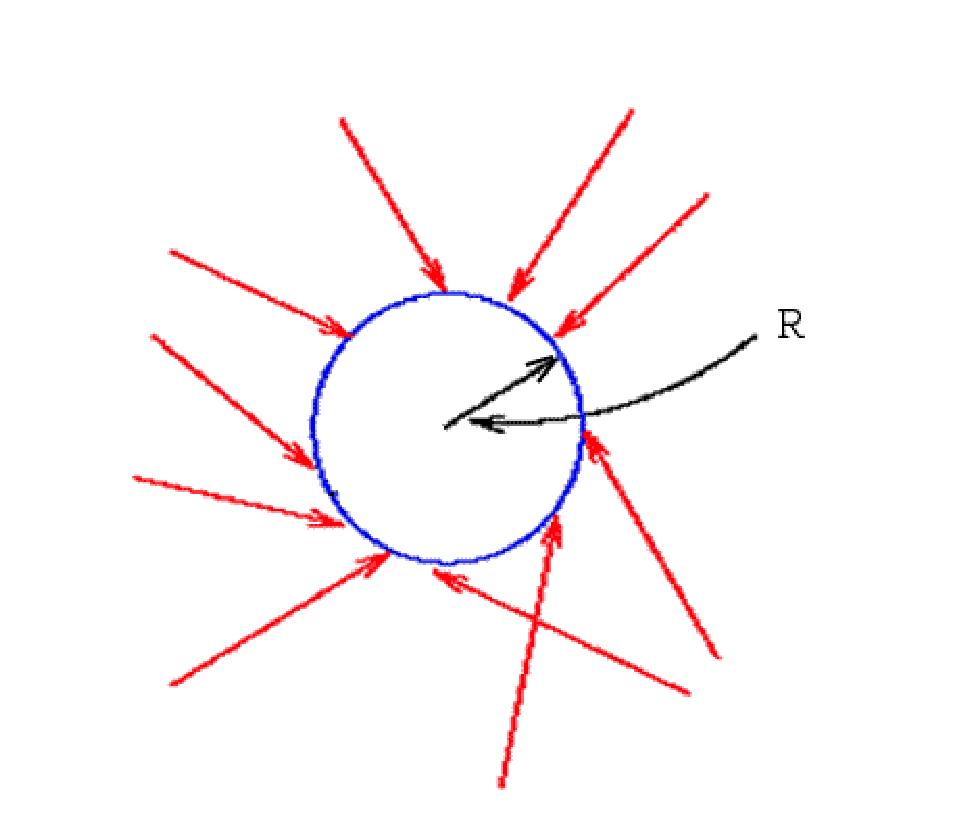
Рис. 24. Счетчик падающих частиц.

из всего потока частиц те, которые падают на поверхность сферы снару­жи.

Если размеры детектора малы, то изменением дифференциальной плот­ности потока частиц на его поверхности можно пренебречь и вынести Ф из под знака интеграла по поверхности, который после этого может быть вычислен. Он равен площади поперечного сечения сферы:

/ \(Пп)\ ds = AS = ttR ² .

(Ωn)<0

Таким образом,

I_N(t) = <&{r,t) AS,

где

Ф(г;t) = ^^ = f d£l f dE Ф(г,й,Е,t) (40)

- плотность потока частиц в точке г в момент времени t - количество частиц, падающих в единицу времени на поверхность сферы с единичным поперечным сечением.

Плотности потока (40) можно дать и другое физическое толкование. Для этого вычислим суммарный путь, который проходят частицы внутри сферы малого радиуса. Эта величина описывается формулой, аналогич­ной (39):

I_s(t)=fdnfdE f ds\{Un)\<&{f,U,E,t)l{f,U),

(Ωn)<0

6.4. Основные характеристики радиационных полей

65

где /(г, Q) - лучевые размеры детектора для частиц с направлением дви­жения Q, падающих на сферу в точке г (рис. 25).

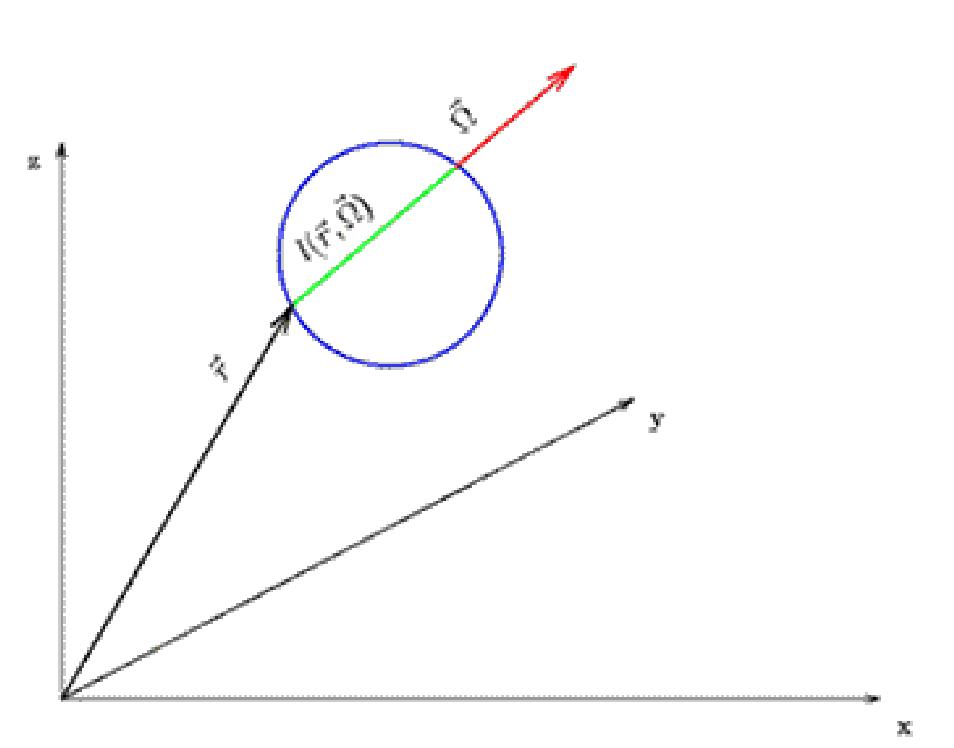
Рис. 25. Лучевые размеры детектора.

Для малого детектора изменением дифференциальной плотности по­тока частиц в его объеме можно пренебречь, и интеграл по поверхности легко вычисляется:

/ |(Ш)| 1(г,П) ds = AV,

(Qn)<0

где AV - объем детектора. Поэтому с учетом (40)

Is{?,t) = AV Ф(г,£),

W,t)

то есть

Ф(г,£) = lim

ду-о AV

Это значит, что плотность потока можно интерпретировать как путь ча­стиц в единице объема в единицу времени.

В некоторых задачах важно знать не количество частиц, падающих на детектор, а их суммарную энергию. Легко видеть, что поток энер­гии определяется такими же формулами, что и поток частиц, если в них дифференциальную плотность потока частиц Ф заменить на произведение Е Ф. Например, количество энергии, падающей на сферический детектор в единицу времени, равно

I_E(t)

dQ

dQ dE

ds \{Un)\ ЕФ(г_}П_}Е_}г).

(Qn)<0

(41)

66 6. Основные понятия теории переноса частиц

Для малого детектора эта формула принимает вид

I_E(t) = I(f,t)As,

где

/(f,t)= f dQ fdE ЕФ{г,П,Е,t) (42)

- плотность потока энергии в точке f в момент времени t, которая на­зывается интенсивностью излучения и представляет собой количество энергии, падающей в единицу времени на поверхность сферы с единич­ным поперечным сечением.

Интегрируя выражения (40), (42) по времени от 0 до Т, можно найти количество частиц и количество энергии, которые падают на детектор за время наблюдения Т. Эти величины называются флюенсом частиц и флюенсом энергии частиц, соответственно.

Интегралы от дифференциальной плотности потока

<&(f,E,t)= [<&{f,U,E,t) dQ

и

Ф(гД*)= [<&{f,U,E,t) dE

называются, соответственно, спектром частиц и угловым распределени­ем частиц в точке г в момент t. Иногда их называют дифференциальной по Е и дифференциальной по П плотностью потока частиц. Их физи­ческий смысл определяется аналогично смыслу величин (40) или (42).

Детектор числа столкновений. Через дифференциальную плот­ность потока частиц можно выразить количество столкновений, происхо­дящих в единицу времени в чувствительном объеме детектора V. Для этого напомним, что дифференциальная плотность потока - это путь, который проходят частицы, находящиеся в единичном объеме фазово­го пространства, в единицу времени, а макроскопическое сечение - это количество столкновений на единице пути. Поэтому показание детектора числа столкновений равно интегралу от произведения дифференциаль­ной плотности потока на сечение по объему детектора, по всем энергиям и всем направлениям движения:

I_c{t)= fdtt f dE [dVY,{E)<&{f,U,E,t). (43)

v

Для детектора малого объма AV, когда изменением функции Ф в нем можно пренебречь,

6.4. Основные характеристики радиационных полей 67

I_c(t) = AV F(f,t), где

F(r,t)= f dQ [ dEY,(E)$(r,U,E,t) (44)

- плотность столкновений - количество столкновений в единичном объ­еме в единицу времени.

Заменяя величину Т,(Е) в формуле (44) на Т,_С(Е) или T,_s(E), мы по­лучим плотность поглощений или плотность рассеяний - количество поглощений или количество рассеяний в единице объема в единицу вре­мени.

Перечисленные выше величины часто называют потоковыми харак­теристиками радиационных полей. Однако в некоторых задачах исполь­зуются другие - токовые характеристики.

Токовые характеристики радиационных полей. Важным поня­тием в теории электричества является сила тока, которая определяется как величина заряда, пересекающего поперечное сечение проводника в единицу времени. Аналогичная характеристика используется и в теории переноса частиц, где током частиц через поверхность S называется раз­ность

J = J₊-J_,

где J+ и J_ - прямой и обратный ток частиц (рис.26). Прямой ток -

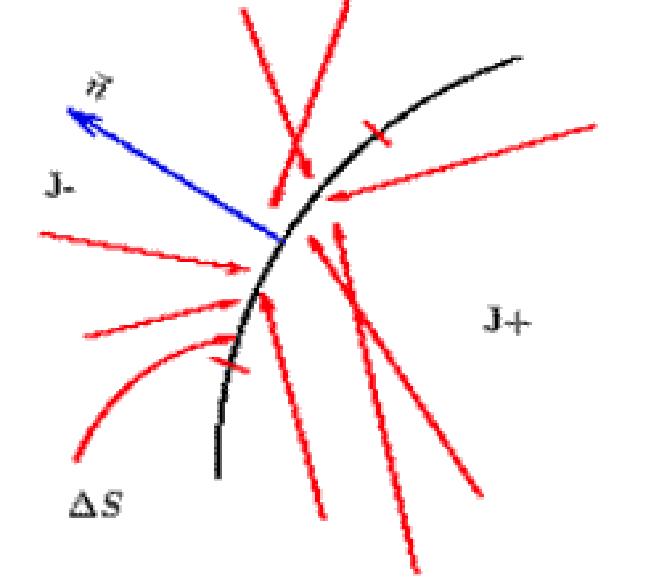
Рис. 26. Ток частиц.

это количество частиц, пересекающих в единицу времени некоторую по­верхность S в положительном направлении. У этих частиц угол между направлением движения и нормалью к S в точке пересечения - острый. Для частиц обратного тока этот угол тупой.

68

6. Основные понятия теории переноса частиц

Используя формулу (38), ток частиц можно выразить через диффе­ренциальную плотность потока Ф(г, Q, Е, t):

J(t) = (dQ fdE Ids (Un) Ф(гД £,£).

s

В этом интеграле область, где (Qn) > 0, соответствует прямому току, тогда как для обратного тока (Un) < 0.

Плотностью тока в теории электричества называют вектор, направ­ление которого указывает направление движения заряда, а величина рав­на количеству электричества, пересекающего в единицу времени единич­ную площадку, перпендикулярную направлению движения. Дифференци­альная по Q и Е плотность тока частиц в точке г в момент t в теории переноса определяется формулой

j(f, Q, E,t) = Q Ф(г, Q, E,t),

а интегралы от нее

j(f, E,t) = f П Ф(г, U, Е, t) dQ

и

j(f, U,t)= f П Ф(г, U, Е, t) dE

называются дифференциальной по Е и дифференциальной по U плотно­стью тока частиц, соответственно.

Плотностью тока частиц в точке г в момент t называют вектор

Э\Т

t) = f dQ f dEU$(r,U,E,t).

Ток частиц J выражается через дифференциальную плотность тока j формулой

J(t)= fftj(f,E,t)ds. s Показания аддитивного детектора. Функция чувствительно­сти детектора. При решении задач теории переноса частиц часто пред­полагают, что показания детектора могут быть записаны в виде суммы вкладов отдельных столкновений в его чувствительном объеме (аддитив­ный детектор). Если вклад от столкновения частицы с энергией Е и на­правлением движения Q в момент t обозначить q(f, Q, Е, t), то показания

6.4. Основные характеристики радиационных полей

69

такого детектора имеют вид интеграла по времени регистрации частиц, по объему детектора, по всем энергиям и всем направлениям движения от произведения числа столкновений на вклад одного столкновения:

I_A= fdtfdQ I dE (dV q(f,U,E,t)T,(E) $>(f,U,E,t). (45)

v

Эту формулу можно переписать в виде

I_A= fdtfdQ I dE (dV D(f,U,E,t)$>(f,U,E,t), (46)

v

где

D(f_}U_} E_} t) = q(f, U,E,t) £(£) (47)

- функция чувствитеьности детектора - вклад в показания детектора от единицы пути частицы в чувствительном объеме детектора.

Подынтегральное выражение в (46) представляет собой произведение пути частиц из единичного объема фазового пространства на вклад в сигнал детектора от единицы пути частицы.

Из (43) видно, что для детектора числа столкновений D(f,U,E,t) = Т,(Е). Для детектора поглощенной энергии D(F, U, Е, t) = (3(E), где /3(E)

- тормозная способность вещества (35).

Если детектор измеряет характеристики потока частиц, падающих на его поверхность S (поверхностный детектор), то интеграл по чувстви­тельному объему в формуле (46) заменяется на интеграл по его поверх­ности:

I_s= fdtfdQ I dE f ds D(f,U,E,t) $>(f,U,E,t). (48)

s

Для точечного детектора, измеряющего локальные характеристики радиационного поля, такие как плотность потока частиц или интенсив­ность излучения, в точке г* функция чувствительности будет иметь мно­жителем ^-функцию:

D(f₎ U, Е, t) = 6(f- 7*)D_r{U, Е, t).

70

6. Основные понятия теории переноса частиц

Вопросы

92. Объясните смысл терминов ”фазовые координаты”, ”фазовое про­странство” и ”элементарный фазовый объем”.

93. Объясните физический смысл понятия ”дифференциальная плот­ность источников”. Перечислите простейшие типы источников.

94. Объясните физический смысл понятий ”сечение взаимодействия”, ”сечение рассеяния”, ”сечение поглощения”.

95. Объясните физический смысл понятия ”дифференциальное сечение взаимодействия”. Перечислите типы дифференциальных сечений.

96. Объясните физический смысл понятий ”макроскопическое сечение взаимодействия”, ”дифференциальное макроскопическое сечение вза­имодействия”.

97. Объясните физический смысл понятий ”дифференциальная плот­ность частиц”, ”дифференциальная плотность потока частиц”.

98. Запишите и объясните формулу для показаний счетчика числа па­дающих частиц и их суммарной энергии.

99. Объясните физический смысл понятий ”плотность потока частиц” и ”интенсивность излучения”.

100. Запишите и объясните формулу для показаний счетчика числа столк­новений.

101. Перечислите основные токовые характеристики поля излучения и объясните их физический смысл.

102. Запишите и объясните формулу для показаний аддитивного детек­тора.

103. Объясните физический смысл понятия ”функция чувствительности детектора”. Приведите примеры.

104. Запишите и объясните формулу для показаний поверхностного де­тектора.

Упражнения 71

Упражнения

105. Объяснить физический смысл подинтегральных выражений в фор­мулах для показаний счетчика падающих частиц, детектора числа столкновений и в общей формуле для показаний аддитивного детек­тора.

106. Доказать, что

/ \Un\ ds = AS,

Un<0

f 1(г,П) \Пп\ ds = AV.

3. Записать формулу для вычисления плотности потока и интенсивно­ сти излучения в точке г* и определить вид соответствующих функ­ ций чувствительности.

Задачи

107. Частица с прицельным параметром р падает вдоль оси Oz на сфери­ческий детектор радиуса R. Вычислить лучевые размеры детектора.

108. Однородный поток частиц падает вдоль оси Oz на сферический де­тектор радиуса R. Вычислить методом статистического моделиро­вания среднее значение прицельного параметра р и средние лучевые размеры детектора.

109. Для предыдущей задачи найти распределение частиц по прицель­ному параметру и по лучевым размерам.

Проблемы

110. Плотность распределения источников. Полное и дифференциальное сечения взаимодействия. Макроскопические коэффициенты взаимо­действия.

111. Основные характеристики радиационных полей. Функция чувстви­тельности детектора.

7. Сечения взаимодействия основных электромагнитных процессов

7.1. Взаимодействие заряженных частиц с веществом

Основными процессами взаимодействия заряженных частиц с веще­ством являются упругое и неупругое рассеяние, а также тормозное излу­чение.

Сечения упругого рассеяния. Кулоновская энергия взаимодействия налетающей заряженной частицы с атомом представляет собой сумму энергий взаимодействия с ядром и электронной оболочкой. В большин­стве задач переноса атомное ядро можно считать точечным, поэтому пер­вый член энергии взаимодействия ведет себя как 1 /г, где г - расстояние между частицей и атомом. При малых г этот член является основным, то есть электрическое поле, создаваемое атомом, практически совпадает с полем ядра. Но на больших расстояниях из-за электрической нейтраль­ности атома энергия взаимодействия убывает значительно быстрее, чем 1/г, то есть электронная оболочка экранирует атомное ядро.

Учет экранирования иногда производится с помощью феноменологи­ческих потенциалов. Например, с помощью потенциала, предложенного Бором:

Щг) = ^-*, (49)

Г

где ez - заряд налетающей частицы, eZ - заряд ядра атома,

а = aoZ-* (50)

- радиус экранирования, а₀ = ^ = 0.53 10"8см - боровский радиус

водорода, т_е - масса электрона. На малых расстояниях (г <С а), когда экспоненциальный множитель мало отличается от единицы, потенциал Бора ведет себя как zZe^z/r. При г > а он быстро убывает (рис.27). Для практических расчетов формулу (49) удобно переписать в виде

W(r) = zZm_ec^^,

а г/а

где го = 2 = 2.818 10~¹³ см - величина, которая имеет размерность

длины и называется классическим радиусом электрона.

7.1. Взаимодействие заряженных частиц с веществом

73

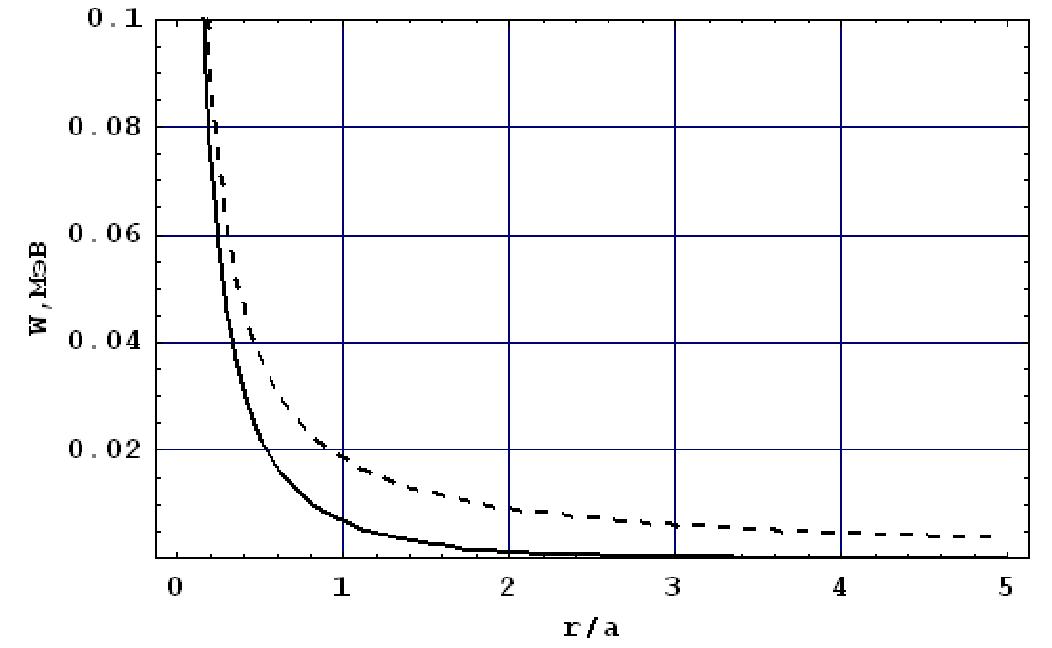
Рис. 27. Энергия взаимодействия а - частицы с атомом Аи. Пунктирная линия - без учета экранирования.

С учетом эффекта экранирования дифференциальное сечение упру­гого рассеяния нерелятивистских частиц имеет вид

1

\Z-F(q)\²

(51)

da_R z²e⁴

dtl 16Щ sin⁴ 6/2

где E_c и О - суммарная кинетическая энергия частиц и угол рассеяния в системе центра инерции, соответственно, F(q) - зависящий от структу­ры электронных оболочек атомный фактор рассеяния. Аргументом этой функции является величина импульса, передаваемого при столкновении:

ТЬО —— Т)п — Т)

где р_с и $_с - импульс налетающей частицы до и после столкновения в системе центра инерции (рис.28).

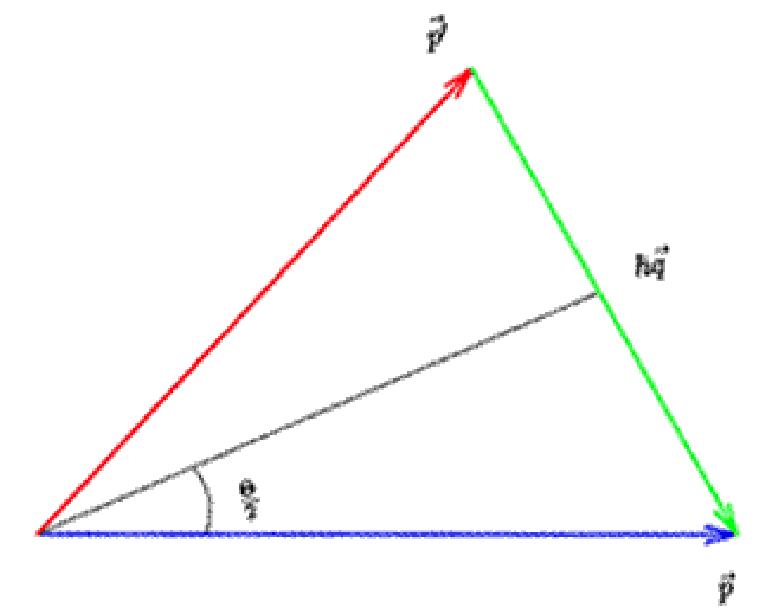
Рис. 28. Передаваемый импульс.

При упругом рассеянии величина импульса не меняется, то есть \р_с \$_с\, поэтому передаваемый импульс связан с углом рассеяния:

в Па = 2р_с sin-. ^{4 Fc} 2

74 7. Сечения взаимодействия основных электромагнитных процессов

Множитель . ₄ в формуле (51) говорит о том, что большая часть

налетающих частиц рассеивается на малые углы, то есть угловое распре­деление сильно вытянуто вперед.

Разность Z - F(q) в формуле (51) можно рассматривать как эффек­тивный заряд ядра, величина которого уменьшена экранированием. При рассеянии на большие углы, что соответствует столкновениям с малым прицельным параметром, F(q) -► 0 (экранирование отсутствует), и фор­мула (51) превращается в формулу Резерфорда, описывающую рассеяние частицы на точечном ядре. Это отражает то, что при рассеянии с малыми прицельными параметрами облако атомных электронов симметрично по отношению к траектории налетающей частицы, поэтому силы, с которы­ми электроны действуют на частицу, взаимно компенсируются, и рассея­ние обусловлено только взаимодействием с ядром. И наоборот, при боль­ших прицельных параметрах, соответствующих малым углам рассеяния, ядро сильно экранируется электронной оболочкой, и сечение оказывается существенно меньше резерфордовского.

Дифференциальное сечение рассеяния, вычисленное с потенциалом Бора (49), имеет вид

dan _ z²Z²e^A 1

dn ~ Щ (1-cos в+ ^2/2)²' ( )

где $_s - угол экранирования, который равен отношению дебройлевской длины волны налетающей частицы А ~ h/p_c к радиусу экранирования.

Энергия Е_с связана с энергией налетающей частицы в лабораторной системе координат Е:

2 т ' где т - масса частицы, /j, - приведенная масса системы частица + атом,

тМ

11 =

т + М'

а М - масса атома. Поэтому формулу (52) можно переписать в удобном для практических вычислений виде:

m + M²

_м

da_R z²Z²rl (т_ес²\2 (т + М\2 1

dQ 4 Е М (1- cos6 + #2/2)2

Импульс налетающей частицы в системе центра инерции р_с выража­ется через импульс в лабораторной системе р:

М

Рс = 11V = Р,

т + М

7.1. Взаимодействие заряженных частиц с веществом

75

поэтому, используя формулу (50) и выражая импульс р через энергию Е: р = уЪпЕ, угол экранирования $_s можно записать в виде

П „_тт + М I т_е/т

17 г, = = (x/i А /

^s р_са М у Е/т_ес²'

е² 1 где а = — = —- - постоянная тонкой структуры. Tie 137 Дифференциальное сечение упругого рассеяния а - частиц на атомах

Аи, вычисленное по формуле (52) с учетом и без учета экранирования, приведено на рис.29. Из рис.29 видно, что экранирование уменьшает ко­личество частиц, рассеянных на малые углы.

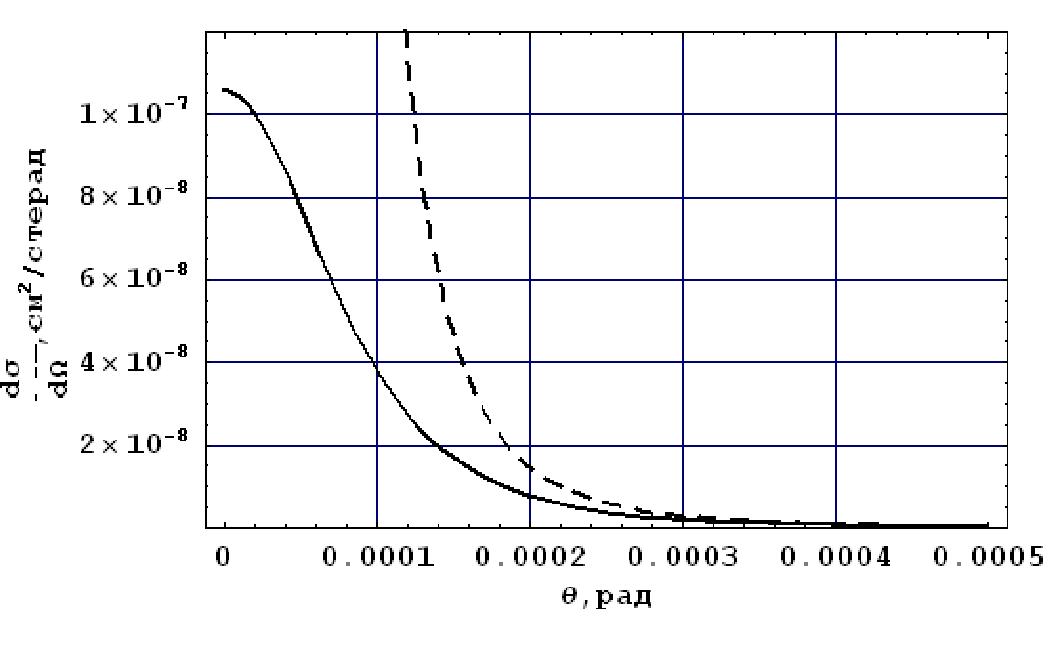
Рис. 29. Дифференциальное сечение рассеяния а - частиц с энергией 4.78 МэВ на атомах Au. Пунктирная линия - без учета экранирования.

Интегрируя дифференциальное сечение по направлениям, получим полное сечение упругого рассеяния:

a_R(E) = z 2 Z4rl ^ ¹¹^^-²

+ М

M #2(1+^2/4)

С ростом энергии частицы оно убывает.

Для релятивистских электронов дифференциальное сечение упругого рассеяния было получено Моттом с учетом их спина. Соответствующие данные обычно приводят в виде отношения сечения Мотта к сечению Резерфорда. Это отношение (множитель Мотта) зависит от атомного номера Z, энергии Е и угла рассеяния G.

Неупругое рассеяние заряженных частиц. В процессе неупруго­го столкновения заряженной частицы с атомом часть ее энергии тратится на возбуждение или ионизацию электронных оболочек. При качественном квазиклассическом описании этого процесса пренебрегают связью атом­ных электронов с ядром и неупругое столкновение с атомом рассматрива-

76 7. Сечения взаимодействия основных электромагнитных процессов

ют как упругое рассеяние на Z атомных электронах. Дискретность энер­гетического спектра атома учитывается введением минимальной энергии / (потенциал ионизации), которую может потерять частица при столк­новении с электроном атома. В этом приближении дифференциальное по потерям энергии Q сечение рассеяния на электроне имеет вид

da_m 7гг²е⁴ т 1 _Т „ „

где m - масса налетающей частицы, Q_max - максимальная энергия, кото­рую может потерять частица при столкновении с электроном:

Е - кинетическая энергия налетающей частицы в лабораторной системе координат.

Полное сечение неупругого рассеяния на i-м электроне получается ин­тегрированием этого выражения по переменной Q:

, nz 2 e^A m /1 1 \ ₉ Jm_ec 2 ) 2 m /1 1 \

^{^Е) = —^ U - qzJ = ^ ^г~с U - q^J • (53)}

Из этой формулы следует, что при

ионизация невозможна. В точке Е = 2E_mi_n функция o~i(E) имеет мак­симум и при увеличении Е - убывает. Зависимость сечения ионизаци К-электрона Au от энергии а-частицы, вычисленная по формуле (53) с k = 80кэВ, приведена на рис.30.

Полное сечение неупругого рассеяния на атоме с Z электронами равно сумме сечений (53):

где /* - средний потенциал ионизации, определяемый формулой

1 1^1

⁼⁼ 7

/* Z^I{

С ростом энергии сечение убывает как 1/Е, потому что с ростом ско­рости частицы уменьшается время ее взаимодействия с атомом.

7.1. Взаимодействие заряженных частиц с веществом

77

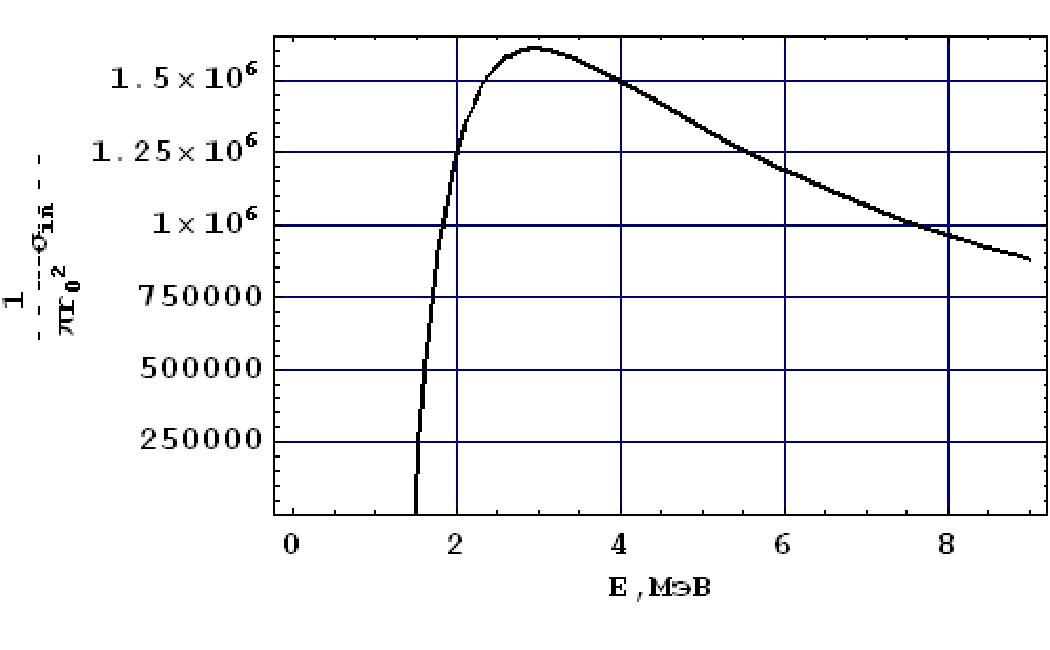
Рис. 30. Зависимость сечения ионизации K-электрона Au от энергии а -частицы.

Угловое распределение частиц после неупругого рассеяния зависит от величины передаваемого импульса. При больших передаваемых импуль­сах q (большие углы рассеяния) сечение неупругого рассеяния совпадает с резерфордовским сечением рассеяния на Z свободных электронах. При малых q сечение ведет себя как I/O² и заметно превосходит сечение упру­гого рассеяния, которое с учетом экранирования выходит на константу при 6^0.

В расчетах методом Монте-Карло неупругие столкновения заряжен­ных частиц с атомами обычно делят на две группы: близкие столкнове­ния, то есть столкновения с большой передачей энергии (Q > Q_t), кото­рые рассматриваются индивидуально и моделируются в соответствии с их сечениями, и далекие столкновения - столкновения с Q < Q_t, которые учитываются в приближении непрерывного замедления. В этом прибли­жении считается, что энергия частицы меняется вдоль траектории непре­рывно, и потери энергии на единице длины пути равны

o_t

P_<(E;Q_t)= f QY,(Q;E)dQ.

о

Для релятивистских частиц потери энергии в далеких столкновениях описываются формулой Бете-Блоха:

_К5^-'

[З^Е- Q_t) = 2^lz²Zn_Q-^p- log

2 2 rn^ 2m_ec²(3²Q_t

/З² °g (1-/3²)Р

где / - средняя энергия возбуждения атомов среды, /3 = v/c, v - скорость налетающей частицы. График функции /3<(£;Q_t) для электронов в Al при Q_t = 500 эВ приведен на рис.31.

С увеличением энергии частицы потери энергии убывают из-за умень­шения времени взаимодействия. Но в релятивистской области энергий они

78 7. Сечения взаимодействия основных электромагнитных процессов

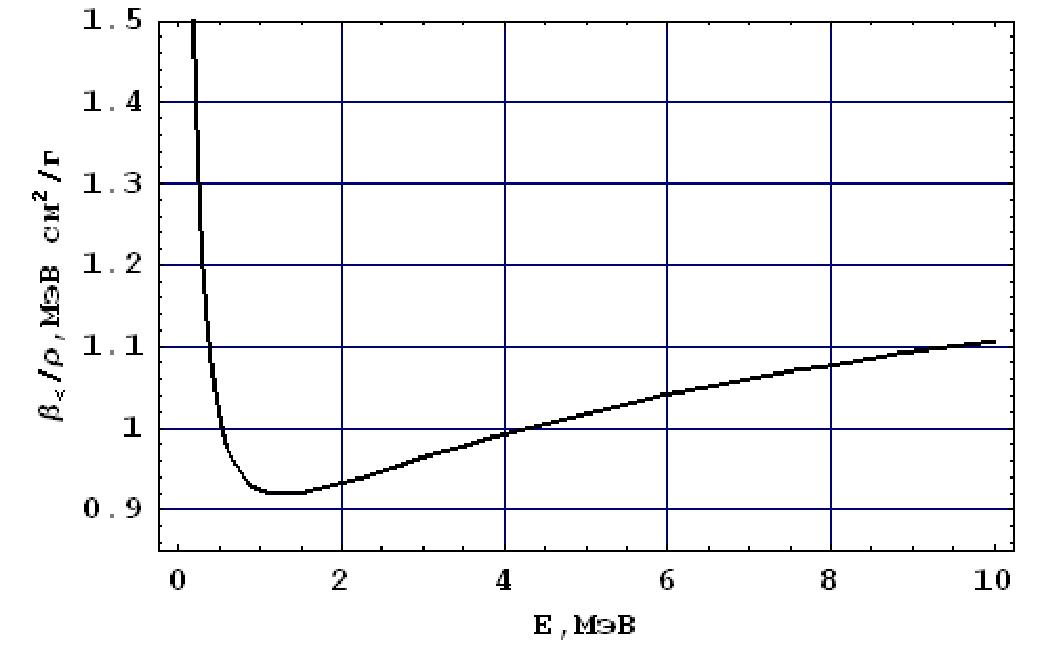
Рис. 31. Потери энергии электронами в Al за счет столкновений с Q_t = 500 эВ.

начинают расти, так как при этом увеличивается величина максимальной энергии, которую может потерять частица при столкновении, а также по­тому, что в соответствии с преобразованиями Лоренца для электромаг­нитных полей растет радиус действия электрических сил и частица вза­имодействует с большим количеством атомов мишени. При дальнейшем увеличении энергии рост потерь замедляется, так как при большом радиу­се действия сил атомы, оказывающиеся в области действия сил, экраниру­ют друг друга и взаимодействие частицы с каждым из них уменьшается. Этот эффект называется эффектом плотности.

Для моделирования близких столкновений релятивистских электро­нов с электронами атома в качестве дифференциального сечения рассея­ния используется формула Меллера, описывающая рассеяние на свобод­ных электронах, то есть без учета их связи с ядром:

do-_M 2ш1 f(l-lf 1/1 2₇

dx /3²(₇ - 1) V 7² х х ₇²

1 1 27-1

Н Ц.— ,

1 — ж 1 — х 7

1/1 27

где х = ;г, 7 = о) Р = ~- График функции — приведен на

Е — т_ес^г т_ес^г с dx

рис.32.

Из рис.32 видно, что преобладающими являются столкновения, при которых Q близко к нулю или к начальной кинетической энергии, то есть когда одна из частиц после столкновения имеет малую энергию. Однако следует отметить, что в квантовой механике при столкновении тожде­ственных частиц вторичной считается частица с меньшей энергией, по­этому относительная потеря энергии х в формуле Меллера изменяется в

интервале (x_t) 1/2), где x_t = — ~.

Ej — 7TL_eC

7.1. Взаимодействие заряженных частиц с веществом

79

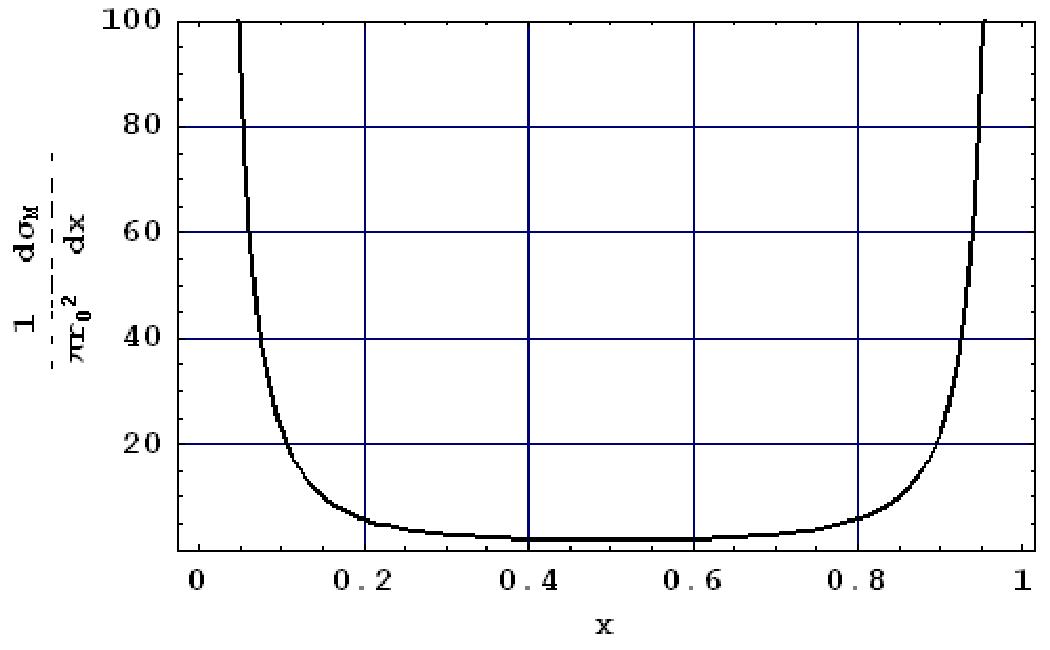
Рис. 32. Дифференциальное сечение рассеяния электронов на электронах. 7 = 10.

Полное сечение столкновений с передачей энергии Q > Q_t, полученное интегрированием формулы Меллера, имеет вид

/3²(₇ 1

(Jm(E; Q_t)

1

2nr 2 Z /(₇-i) 2/i

t

1)

27

-хЛ

x_t

%t H

%t

Г

С ростом энергии оно убывает (рис.33).

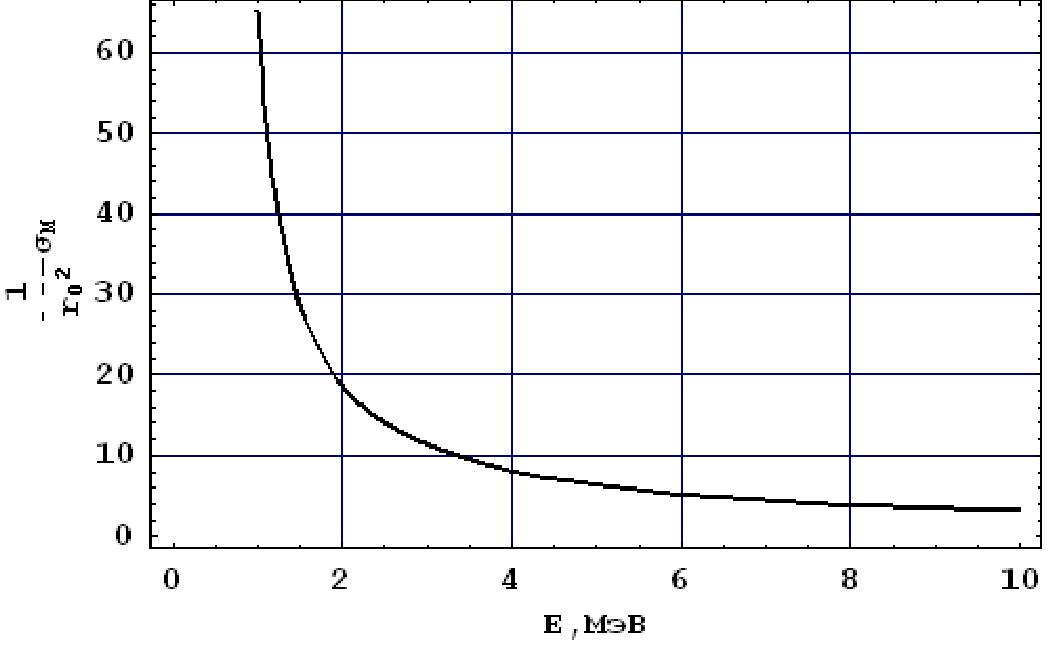
Рис. 33. Зависимость полного сечения меллеровского рассеяния от энер­гии налетающего электрона. x_t = 0.1.

Для тяжелых частиц моделирование потерь энергии в близких столк­новениях проводится с помощью дифференциального сечения, которое зависит от спина налетающей частицы. Для частиц со спином 1/2 оно имееет вид

du_in 2nrlm_ec²Zz² 1 dQ (З² Q²

l-(3²

+

Q Q²

Q_max 2£2

Qt < Q < Q_maXi

80 7. Сечения взаимодействия основных электромагнитных процессов

где

Qmax

2m_ec²(₇² - 1)

1 + 2₇m_e/m + (m_e/m)

- максимальная энергия, передаваемая свободному электрону частицей с массой т. График кривой -^ для протонов приведен на рис.34.

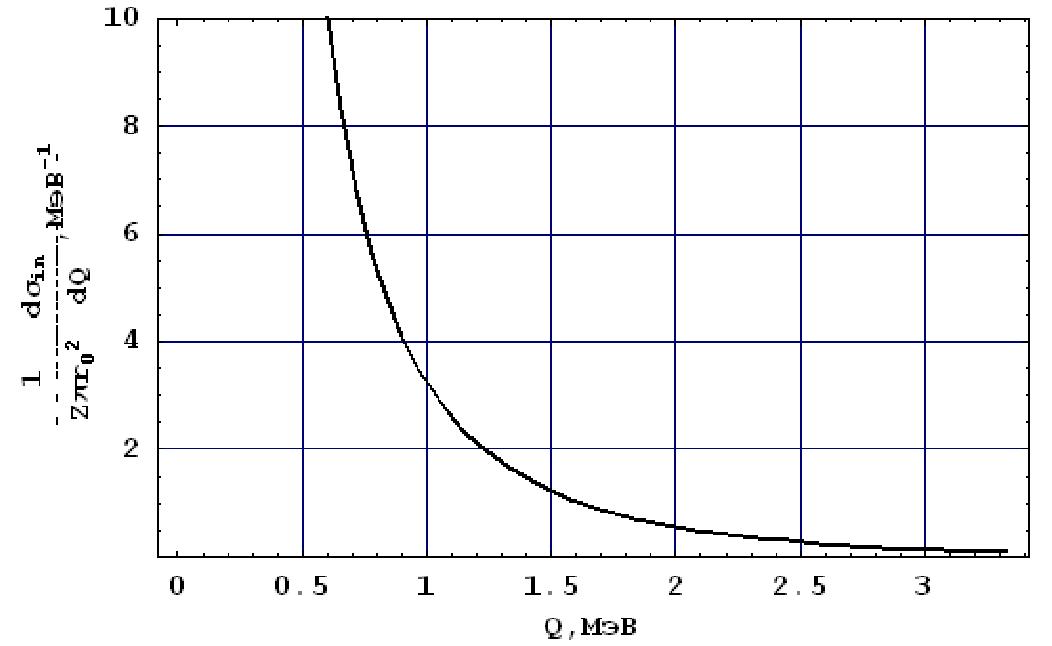
Рис. 34. Дифференциальное сечение неупругого рассеяния протонов с ки­нетической энергией 1000 МэВ.

Для частиц со спином 0

Q

1-/3²-

da_m 2nr²_Qm_ec²Zz² 1

dQ [З² Q² Q_max

Qt<Q< Q_max.

Вид сечения для а-частиц показан на рис.35.

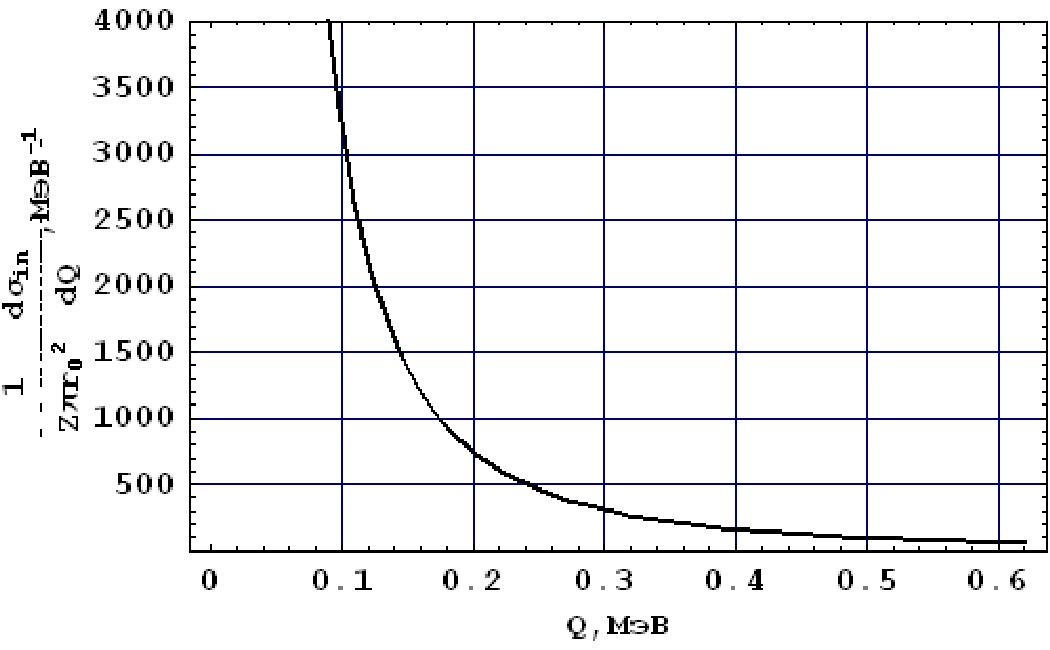
Рис. 35. Дифференциальное сечение неупругого рассеяния а - частиц с кинетической энергией 1000 МэВ.

Полное сечение неупругого рассеяния также зависит от спина: для частиц со спином 1/2

0in(E', Qt)

+

2nrlm_ec²Zz² l-y + {3²ylogy Q_max

[3²

Qt

2E²

Qt\

У

Qt

_QU7X

7.1. Взаимодействие заряженных частиц с веществом

81

и для частиц со спином 0

С ростом энергии налетающей частицы сечение убывает.

Тормозное излучение. В соответствии с законами электродинамики заряженная частица, движущаяся с ускорением, должна излучать элек­тромагнитные волны. Примером является тормозное излучение, которое испускается частицами при прохождении через вещество. Ускорение ча­стицы, взаимодействующей с атомами, обратно пропорционально ее мас­се, поэтому испускание тормозного излучения существенно влияет на дви­жение легких заряженных частиц - электронов и позитронов. Для тяже­лых частиц им обычно пренебрегают.

Тормозное излучение имеет непрерывный энергетический спектр, и энергия испущенных фотонов лежит в интервале 0 < Е₁ < Е, где Е -кинетическая энергия частицы.

На тормозное излучение, как и на рассеяние заряженных частиц, су­щественно влияет экранирование ядра атомными электронами, которое уменьшает эффективный заряд ядра при столкновениях с большими при­цельными параметрами. Макроскопическое дифференциальное сечение тормозного излучения в ультрарелятивистском случае (Е, £", Е₁ ^> тс²) и без учета экранирования описывается формулой Бете-Гайтлера:

о ₂1 Е' Е¹ Е 2

_{AZar^U U + Ё> - з 0°g}

da_{br 2} 1 Я' (Е¹ Е 2\ ( 2ЕЕ'

dE₁ ^VE₇E Е Е' З тс²Е₁ 2

где Е' = Е- Е_Т

В приближении полного экранирования

S-4^if((f+l-8ⁱo^ⁱ83^z-ⁱ/3 )+J)-

Вид дифференциальных сечений тормозного излучения с учетом и без учета экранирования показан на рис.36.

Из рис.36 видно, что сечение является быстро убывающей функцией Е₁ и что экранирование сильно уменьшает количество низкоэнергетиче­ских фотонов.

При качественных оценках иногда считают, что спектр фотонов тор­мозного излучения описывается функцией 1/Е₁.

При решении задач переноса электронов методом Монте-Карло ис­пускание фотонов с энергией выше некоторого порогового значения Q_t моделируется в соответствии с вероятностями, вид которых определяется

82 7. Сечения взаимодействия основных электромагнитных процессов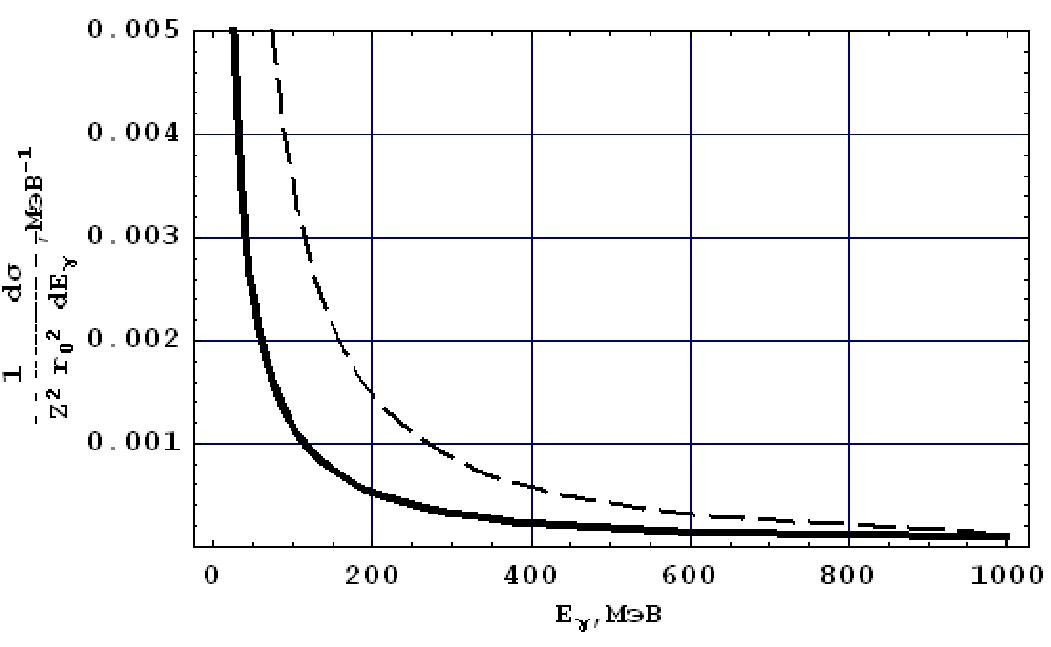

Рис. 36. Дифференциальные сечения тормозного излучения с учетом (сплошная линия) и без учета экранирования (пунктирная линия). Воль­фрам, 1000 МэВ.

дифференциальным сечением процесса, а испускание фотонов меньших энергий рассматривается в приближении непрерывного замедления.

Угловое распределение тормозного излучения релятивистских частиц вытянуто вперед:

da_br 1

то есть сосредоточено, в основном, в конусе с углом раствора ~ тс²/Е около направления движения первичной частицы.

Тормозное излучение может испускаться не только в поле ядра, но и в поле атомных электронов. Однако сечение этого процесса пропорциональ­но числу электронов Z, тогда как сечение на ядре пропорционально Z². Поэтому роль тормозного излучения на электронах может быть заметной только в веществах с малым Z.

7.2. Взаимодействие гамма-квантов с веществом

Основными процессами взаимодействия гамма-излучения с веществом являются фотоэффект, преобладающий в области низких энергий, обра­зование электрон-позитронных пар, важное только при высоких энерги­ях, и комптоновское рассеяние, играющее существенную роль для фото­нов промежуточных энергий.

Комптоновское рассеяние. Электромагнитное излучение, падаю­щее на атом, взаимодействует с его электронной оболочкой. При описании этого процесса в рамках классической физики считается, что ускорение электронов, вызванное взаимодействием, приводит к излучению расходя­щихся от атома электромагнитных волн, которые называют рассеянными волнами. Их частота, очевидно, равна частоте колебаний электронов, ко-

7.2. Взаимодействие гамма-квантов с веществом

83

торая, в свою очередь, равна частоте падающего излучения. То есть ча­стота рассеянного излучения должна быть равна частоте падающей элек­тромагнитной волны. Однако при изучении рассеяния рентгеновского из­лучения экспериментально было обнаружено, что частота излучения при рассеянии уменьшается и величина эффекта (эффект Комптона) растет с увеличением угла рассеяния. Этот результат легко объясняется с кор­пускулярной точки зрения, когда электромагнитное излучение считается потоком частиц - квантов с энергией Е и импульсом р, которые связаны с волновыми характеристиками - частотой си и длиной волны излучения

2тг

Т'

Л:

Е = hcu, р = fik, к

Е

При рассеянии кванта на атомном электроне последнему передает­ся часть энергии налетающего кванта. Если передаваемая энергия много больше энергии связи электрона, то электрон можно считать свободным. В этом случае из законов сохранения энергии и импульса следует, что энергия рассеянного фотона Е' связана с углом рассеяния G соотноше­нием

Е'

(54)

l + (£/m_ec²)(l-cos6)

где т_ес² - энергия покоя электрона. Из рис.37 видно, что относительное изменение энергии фотона растет с увеличением начальной энергии.

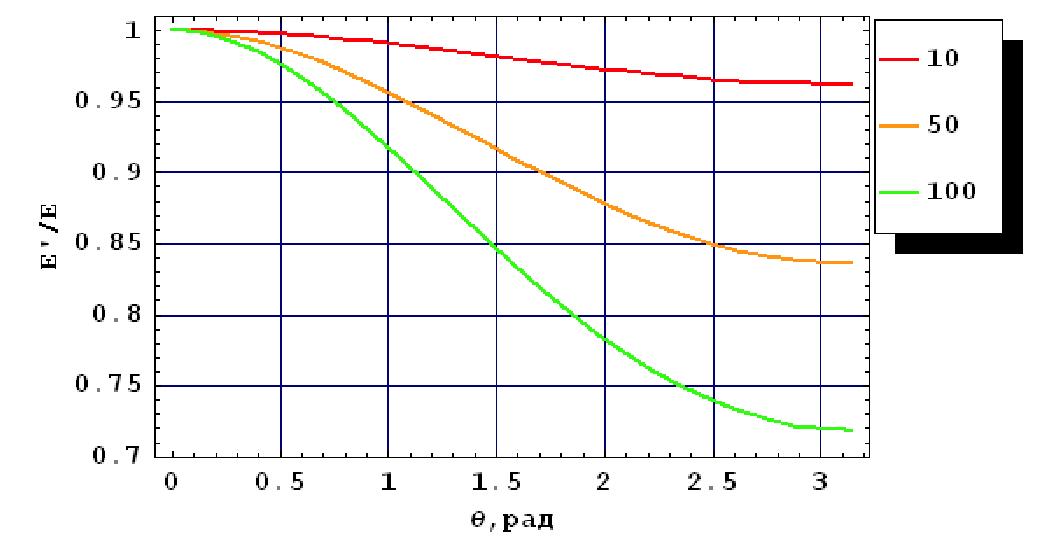
Рис. 37. Изменение энергии фотона при комптоновском рассеянии для £₇ = 10 кэВ, 50 кэВ и 100 кэВ.

Кинетическая энергия электрона (энергия отдачи) равна разности энер­гий фотона до и после рассеяния:

Т = Е-Е',

а угол, под которым летит электрон отдачи, определяется формулой:

Т(Е + т_ес²)

COStf_e

_W'

ET(T + 2m_ec²)

84 7. Сечения взаимодействия основных электромагнитных процессов

Угол отдачи электрона может быть выражен через угол рассеяния кванта:

ctg^a + tgf).

Угловое распределение неполяризованных квантов, рассеянных на сво­бодном электроне, описывается формулой Клейна-Нишины-Тамма:

da_c

г_1Е_ 2 Е

2

Е Е'

sin² в

(55)

где Е' - энергия рассеянного фотона, которая определяется формулой (54).

Из формулы (55) следует, что при рассеянии фотонов низких энергий (Е <С т_ес²), когда в соответствии с (54) Е' « Е, распределение по углам симметрично относительно направления G = 7г/2 (вероятности рассея­ния вперед и назад равны). С увеличением энергии количество фотонов, рассеянных под нулевым углом, остается неизменным, а количество рассе­янных назад - уменьшается, то есть угловое распределение вытягивается вперед (рис.38).

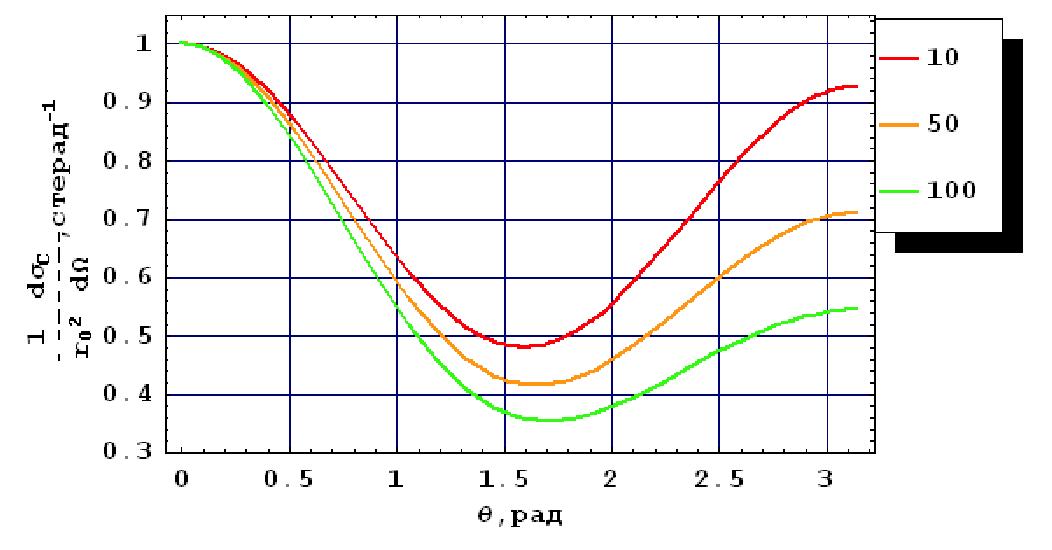
Рис. 38. Дифференциальное сечение комптоновского рассеяния при Е₁ = 10 кэВ, 50 кэВ и 100 кэВ.

Дифференциальное сечение рассеяния гамма-квантов на атоме часто получают, умножая (55) на количество электронов в атоме, пренебрегая тем самым связью электронов с ядром. При более точном рассмотрении следует учитывать, что рассеяние может быть упругим, то есть без изме­нения состояния атома, и неупругим, то есть с возбуждением или иони­зацией атома. Первый тип рассеяния называют когерентным. Энергия фотона при таком рассеянии остается неизменной, так как масса ато­ма велика, и поэтому потеря энергии на отдачу пренебрежимо мала. Во втором случае рассеяние называется некогерентным, и оно происходит с изменением энергии.

7.2. Взаимодействие гамма-квантов с веществом

85

Для когерентного рассеяния, которое преобладает при низких энерги­ях фотонов, дифференциальное сечение рассеяния описывается форму­лой

^ = -(l+cos²e)|F(g)|², dQ 2 ^{v W}

где F(q) - упоминавшийся в п.7.1 атомный фактор рассеяния, который определяется структурой электронной оболочки атома. Если длина вол­ны падающего излучения много больше размеров атома, то F —> Z и

— ~ Z 2 . Это означает, что волны, рассеянные различными электронами,

оказываются в фазе, поэтому амплитуда рассеянной волны увеличивает­ся в Z раз, а сечение возрастает в Z² раз. В другом предельном случае сечение рассеяния на атоме равно сумме сечений рассеяния на отдельных электронах и поэтому пропорционально Z.

Дифференциальное сечение некогерентного рассеяния, относительная роль которого растет с увеличением энергии, обычно представляют в ви­де произведения формулы Клейна-Нишины-Тамма (55) и функции неко­герентного рассеяния S, которая зависит от атомного номера вещества и энергии, передаваемой атому при рассеянии. При больших передачах энергии S —>■ 1, то есть связь электрона с ядром становится несуще-ственой. При малых передачах S —>■ 0, указывая на то, что рассеяние с малыми передачами энергии (малые углы рассеяния) невозможно из-за дискретного характера энергетического спектра атома.

Полное сечение комптоновского рассеяния монотонно убывает с ро­стом энергии фотонов. Без учета связи электронов с ядром оно описыва­ется формулой

,_c(_B) = 2^i((l-|-l)log(l + ,) + I + |-_ml^),

где х = 2 -. Для низкоэнергетических фотонов оно убывает по линей­ ному закону, а в области высоких энергий - обратно пропорционально Е (рис.39).

Фотоэффект. Электромагнитное излучение может поглощаться ато­мами. При этом энергия фотона передается одному из электронов, кото­рый покидает атом. В нерелятивистском приближении угловое распреде­ление фотоэлектронов, выбиваемых с К-оболочки, описывается прибли­женной формулой

da_ph г ₂ 4 5 fm_ec²\^7/2 sin² в

Ж = 2^л/2^Гоа Z [-Ё-) (1-v/ccosSr

86 7. Сечения взаимодействия основных электромагнитных процессов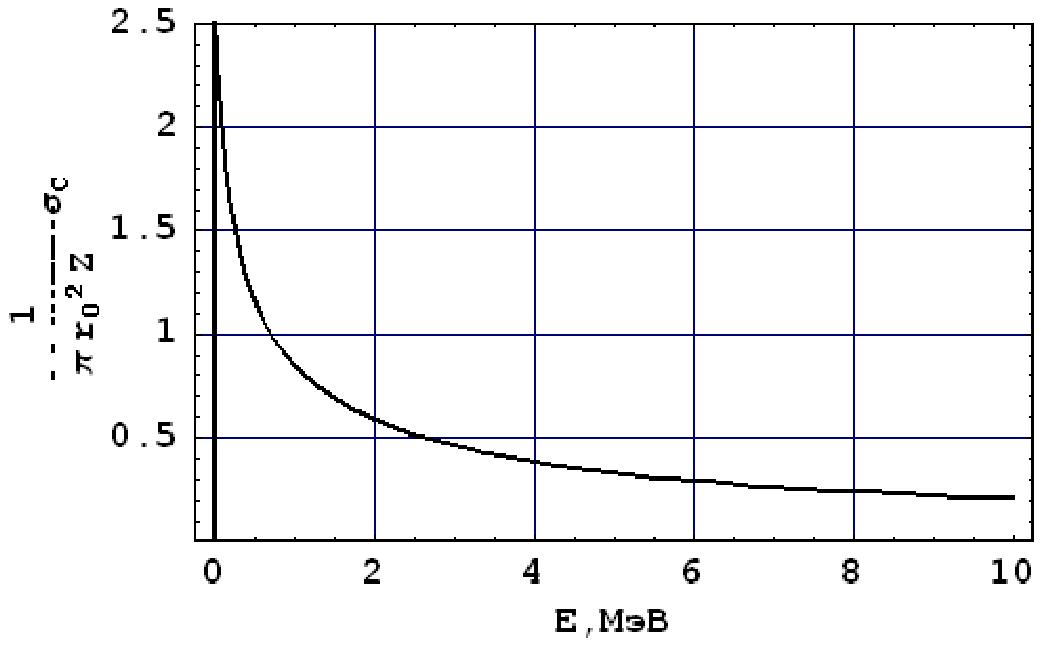

Рис. 39. Зависимость полного сечения комптоновского рассеяния от энер­гии фотона.

где v - скорость фотоэлектрона, которую можно выразить через энер­гию фотона с помощью закона сохранения энергии. Из этой формулы следует, что из-за поперечности электромагнитной волны электроны вы­летают, в основном, перпендикулярно к направлению распространения волны (G ~ тг/2), то есть вдоль вектора напряженности электрического поля. С увеличением энергии квантов максимум углового распределения смещается в сторону меньших углов (рис.40).

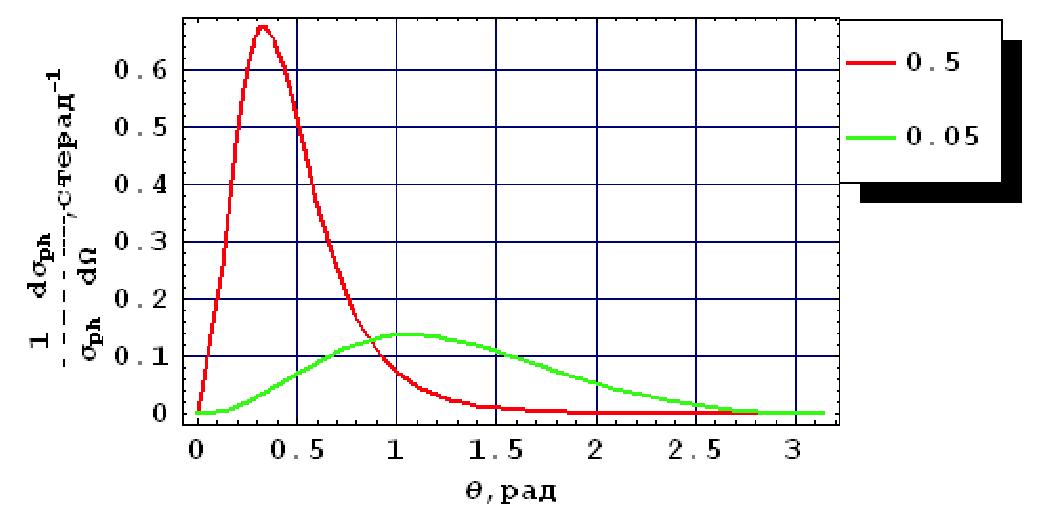
Рис. 40. Угловое распределение фотоэлектронов, выбиваемых из олова фотонами с энергиями 0.05 МэВ и 0.5 МэВ.

Полное сечение фотоэффекта в среднем быстро убывает с ростом Е и растет с увеличением атомного номера вещества:

где п ~ 3 при низких энергиях (Е < 150 кэВ) ип~1 при высоких энер­гиях (Е > 5 МэВ), а т меняется от 4 при Е = 100 кэВ до 4.6 при Е = 3 МэВ. Такое поведение сечения обусловлено тем, что с ростом энергии фо­тона и уменьшением Z уменьшается относительная роль связи атомного электрона с ядром, а поглощение фотона свободным электроном запре­щено законами сохранения энергии и импульса. Поэтому, чем больше Е

7.2. Взаимодействие гамма-квантов с веществом

87

и меньше Z, тем меньше вероятность фотопоглощения. По той же при­чине наиболее вероятным является выбивание электронов с самых ниж­них оболочек. У тяжелых атомов около 80% фотоэлектронов выбивается с K оболочки.

Следует, однако, иметь в виду, что процесс фотопоглощения имеет по­роговый характер - энергия фотона должна быть больше энергии связи электрона в атоме, поэтому в области низких энергий энергетическая за­висимость фотоэффекта имеет характерную пилообразную форму с рез­кими краями поглощения на пороге ионизации каждой электронной обо­лочки (рис.41).

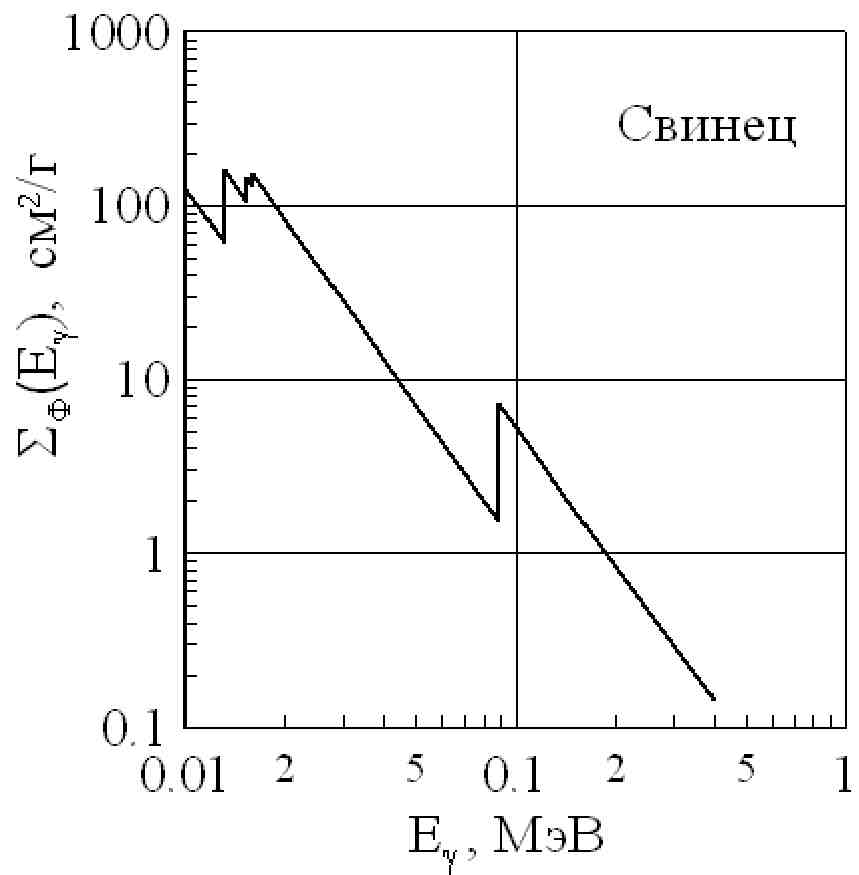
Рис. 41. Сечение фотоэффекта для свинца.

Кинетическую энергию фото-электрона Т можно найти из закона со­хранения энергии

Т = Е-1_Ь,

где 1_Ъ - энергия связи электрона на внутренней оболочке атома. Энергия связи электрона на К—оболочке равна 13.6 эВ для водорода, 7.11 кэВ для железа, 88 кэВ для свинца и 116 кэВ для урана.

Образование электрон-позитронных пар. Если энергия фотона превышает пороговое значение 2т_ес², то при столкновении с ядром он может превратиться в электрон-позитронную пару:

7 ->• е" + е⁺.

При этом

Е₁ = Е_ + Е₊,

где Е- и Е₊ - полные энергии электрона и позитрона.

88 7. Сечения взаимодействия основных электромагнитных процессов

Дифференциальное по энергии вторичных частиц сечение образова­ния пар симметрично относительно энергий электрона и позитрона и в ультрарелятивистском случае без учета экранирования имеет вид

£"»-**(«f**I"0(*!SSH)-

При полном экранировании

^ = < a Z²-^ (е²₊ + Е²_ + \е-е\ (log (183Z"¹/³) - ±) .

Вид дифференциальных сечений образования электрон-позитронных пар с учетом и без учета экранирования показан на рис.42.

Рис. 42. Дифференциальное сечение образования электрон-позитронных пар без учета (сплошная линия) и с учетом (пунктирная линия) экрани­рования. Вольфрам, £₇ = 100 МэВ.

Из рис.42 видно, что эффект экранирования существенно изменяет количество низкоэнергетических частиц.

Полное сечение образования пар без учета экранирования имеет вид

а_р(Е,) = aZ 2 r 2 (™ log^ - ™\ .

Оно растет с ростом энергии кванта (рис.43).

В приближении полного экранирования сечение не зависит от энергии:

а_р(Е,) = aZ²rl (flog (183Z"¹/³) - |Л .

Для фотонов высокой энергии направления импульсов вторичных ча­стиц, как и в случае тормозного излучения, лежат в узком конусе около

т_ес² первичного направления с углом раствора ~ ——.

Вопросы

89

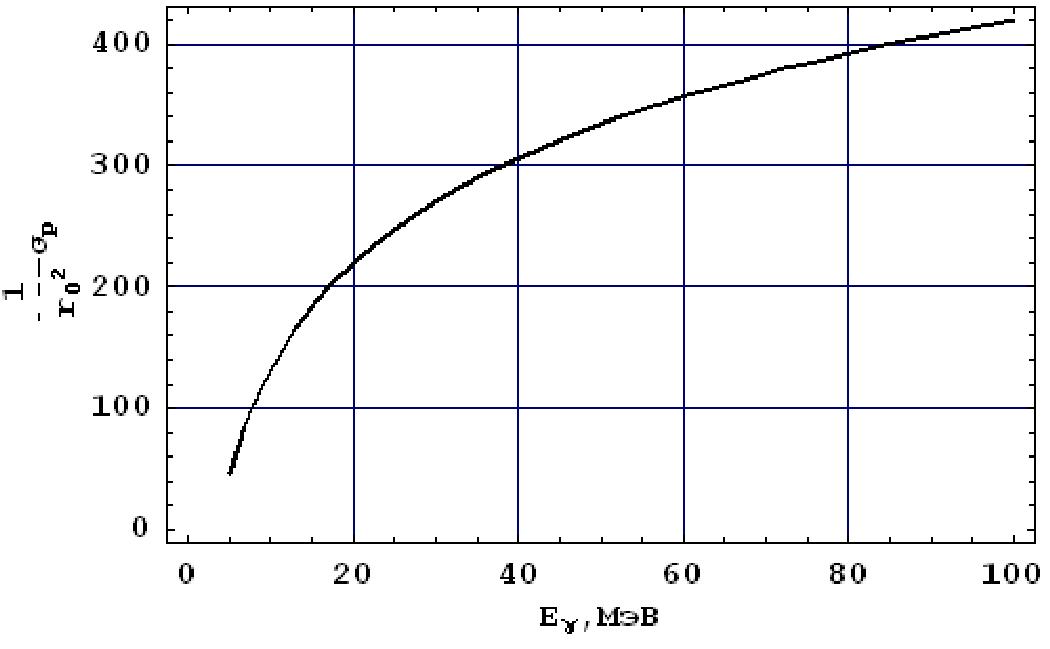
Рис. 43. Зависимость полного сечения образования электрон-позитронных пар от энергии фотона (без учета экранирования). Вольфрам.

Так же, как генерация тормозного излучения, рождение электрон-позитронных пар возможно в электрическом поле атомных электронов. Пороговая энергия этой реакции равна 4m_ec², а сечение меньше, чем се­чение в поле ядра, и в расчетах им часто пренебрегают.

Вопросы

112. Объясните физический смысл термина ”экранирование”. Как влияет этот эффект на вид энергии взаимодействия налетающей частицы с атомом и на дифференциальное сечение упругого рассеяния?

113. Опишите квазиклассическую модель неупругого рассеяния заряжен­ных частиц на атомах.

114. Объясните, как зависит сечение ионизации от энергии налетающей частицы.

115. Объясните, как зависит ионизационная тормозная способность ве­щества от энергии налетающей частицы и атомного номера мишени.

116. Объясните смысл термина ”приближение непрерывного замедления”.

117. Опишите процесс тормозного излучения и его основные характери­стики.

118. Назовите основные процессы взаимодействия электромагнитного из­лучения с веществом.

119. Опишите механизм рассеяния электромагнитного излучения с вол­новой и корпускулярной точки зрения.

90 7. Сечения взаимодействия основных электромагнитных процессов

9. Опишите процессы когерентного и некогерентного рассеяния элек­тромагнитного излучения и их основные особенности.

120. Опишите механизм и основные особенности фотоэффекта.

121. Опишите механизм и основные особенности процесса образования электрон-позитронных пар.

122. Опишите зависимость полных сечений взаимодействия гамма-излучения с веществом от энергии квантов.

Задачи

1. Построить график индикатрисы резерфордовского рассеяния — ^

<тд ail с учетом экранирования. Исследовать, как меняется вид этой кри­вой с изменением энергии частицы.

123. Исследовать на экстремум и построить график сечения неупругого рассеяния заряженной частицы на электроне ai_n(E).

124. Построить график дифференциального сечения тормозного излуче­ния с учетом и без учета экранирования.

125. Построить график индикатрисы тормозного излучения —£-. Ис-

а_Ъг ail следовать, как меняется вид этой кривой с изменением энергии элек­трона.

126. Построить график функции Е'/Е для комптоновского рассеяния. Исследовать, как меняется вид этой кривой с изменением энергии фотона.

127. Построить график дифференциального сечения комптоновского рас­сеяния. Исследовать, как меняется вид этой кривой с изменением энергии фотона.

128. Построить график индикатрисы фотоэффекта. Исследовать, как меняется вид этой кривой с изменением энергии фотона. Скорость фотоэлектрона выразить через энергию фотона с помощью нереля­тивистского закона сохранения энергии.

129. Построить график дифференциального сечения процесса образова­ния пар с учетом и без учета экранирования.

Проблемы

91

Проблемы

130. Общая характеристика процессов взаимодействия заряженных ча­стиц с веществом.

131. Общая характеристика процессов взаимодействия гамма-квантов с веществом.

8. Моделирование траекторий частиц. Оценка характеристик радиационных полей

8.1. Вероятностный смысл коэффициентов

взаимодействия. Моделирование траекторий частиц

Прохождение частицы через вещество является типичным приме­ром случайного процесса, состоящего из отдельных случайных элементов: длина пробега между столкновениями, тип взаимодействия, угол рассея­ния. Статистически устойчивая часть каждого из них выражается через макроскопические сечения взаимодействия, что позволяет проводить их компьютерное моделирование.

Моделирование пробега. В п.4.1 было показано, что пробег части­цы между столкновениями случаен. При этом коэффициент ослабления (макроскопическое сечение взаимодействия) равен вероятности столкно­вения на единице пути, а плотность вероятности пробегов имеет вид

w{l) = Е e"^s/, 0 < I < оо.

Моделирование случайных чисел из этого распределения, то есть модели­рование пробега, можно проводить методом функции распределения по формуле

/ = -i 1п₇, (56)

где 7 - случайные числа, равномерно распределенные в (0,1).

Моделирование типа взаимодействия. Тип очередного взаимо­действия частицы тоже случаен. Но из физического смысла макроскопи­ческих сечений и очевидной формулы

Е = £_с + S_s

следует, что р_с = — и p_s = — есть вероятности поглощения и рассеяния,

соответственно. Поэтому, отложив эти величины на отрезке (0,1), по рав­номерно распределенному случайному числу 7 можно моделировать тип взаимодействия.

Моделирование рассеяния. Энергия и направление движения ча­стицы после рассеяния случайны, и вид энергетического и углового рас­пределений определяется соответствующими дифференциальными сече­ниями.

8.1. Вероятностный смысл коэффициентов взаимодействия... 93

Плотность вероятности случайного значения энергии Е' после рассе­яния равна

ЦЕ';Е)

_{w{e'e) = ^XeV}

Макроскопические сечения основных взаимодействий хорошо известны, что позволяет использовать эту формулу для моделирования случайного Е' одним из описанных ранее методов.

Из физического смысла макроскопического дифференциального по О! сечения рассеяния следует, что вероятность рассеяния Г2 —> ГУ (ГУ G (Ю) равна

В сферических координатах

dtt' = sinQdQd(p.

В задачах с азимутальной симметрией рассеяния, когда дифференциаль­ное по ГУ сечение рассеяния не зависит от азимута (р, мы будем писать

E(fi';fi,£) = E(cosG;£),

где cos О = (Q'Q). Тогда вероятность P(Q' G dQ!) можно записать в виде произведения двух сомножителей, один из которых есть вероятность рассеяния с О G dQ, а второй - вероятность рассеяния с р <Е dp :

P(Q'_e^2,s_lne^s<gg^g>_rfeg.

Соответствующие плотности вероятности равны

_№(co_Se;_B)^2.s_lneHg|^,

w{p) = —.

При известных сечениях взаимодействия эти плотности вероятности ис­пользуются для моделирования полярного угла и азимута, которые опре­деляют направление движения частицы после рассеяния.

Из законов сохранения энергии и импульса для упругого столкновения следует, что энергия рассеянной частицы однозначно связана с углом рас­сеяния. Поэтому при моделировании такого столкновения разыгрывается только одна из этих характеристик, а вторая находится из кинематики рассеяния.

94 8. Моделирование траекторий частиц. Оценка характеристик...

Моделирование траекторий частиц. Траектория частицы в веще­стве состоит из случайных элементов: длина пробега между взаимодей­ствиями, тип взаимодействия, новое направление движения после рас­сеяния. Плотности вероятности для этих элементов выражаются через макроскопические сечения формулами, приведенными выше, поэтому по­следовательное моделирование этих элементов позволяет строить траек­торию от точки рождения до поглощения. Если поглотитель ограничен, то траектория обрывается не только при поглощении, но и при вылете частицы из него.

В реальной задаче место рождения частицы, ее начальная энергия и направление движения могут быть случайными. В этом случае моде­лирование траектории должно начинаться с моделирования начальных значений этих параметров частицы, и для этого необходимо знать плот­ность вероятности начальных фазовых координат г, Q, Е. В качестве этой функции используют нормированную на единицу дифференциаль­ную плотность источников S(f, Q, Е, t).

8.2. Особенности моделирования траекторий заряженных частиц

Распространение заряженных частиц в веществе имеет ряд характер­ных особенностей, которые не позволяют непосредственно моделировать их траектории с помощью метода Монте-Карло. Эти частицы движутся в веществе, не поглощаясь и теряя энергию в упругих и неупругих столкно­вениях, пока их скорость не снизится до тепловой, когда частицу можно считать остановившейся. Определяющую роль в торможении заряженных частиц играет медленно убывающее с расстоянием кулоновское взаимо­действие с атомами, из-за чего в большей части столкновений частица отклоняется на малый угол и теряет малую часть своей энергии. Вслед­ствие этого количество столкновений на траектории столь велико, что их прямое моделирование даже на современных вычислительных маши­нах становится практически нецелесообразным. Исключением являются задачи, где толщина поглотителя очень мала.

Указанные трудности обходят, используя метод группировки столк­новений. При этом истинный путь частицы разбивают на отрезки длины I, которая может быть как детерминированной, так и случайной. Фазовые координаты частицы на этом пути меняются случайным образом, и со­ответствующая плотность вероятности перехода P(f,Q,E —>■ г*, ГУ, Е'\1) удовлетворяет кинетическому уравнению, которое называется уравнени­ем Колмогорова- Чепмена. При малых I это уравнение может быть решено аналитически, и полученное решение используется для моделирования

8.3. Оценка характеристик поля излучения

95

фазовых координат в конце отрезка. Эти координаты, в свою очередь, используются в качестве начальных для розыгрыша координат в конце следующего отрезка и т.д. Моделирование продолжается до тех пор, по­ка энергия частицы остается выше некоторого порогового значения, за которым частицу можно считать остановившейся.

Полученная таким образом последовательность фазовых координат называется вложенной траекторией. В отличие от обсуждавшихся ра­нее траекторий, где узлами были точки столкновений частиц, переход из одного узла вложенной траектории в другой происходит в результате мно­гократного рассеяния на отрезке. Расстояние между узлами вложенной траектории называют геометрическим путем.

8.3. Оценка характеристик поля излучения

Приближенное вычисление (оценку) характеристик поля излучения в простейших случаях можно проводить в процессе моделирования траек­торий, используя определение или физический смысл вычисляемой вели­чины. Например, для оценки коэффициента ослабления излучения плос­кой защитой или коэффициента отражения от нее необходимо промоде­лировать N траекторий частиц и найти количество прошедших N₊ и от­раженных N_ частиц. Отношение N_/N будет оценкой коэффициента отражения, а N+/N - оценкой коэффициента ослабления.

Оценку углового распределения частиц, вылетевших из слоя, можно получить, если область изменения углов вылета 0 < Θ < 7г/2 разделить на малые интервалы ∆Θ и количество частиц с углами Θ G ∆Θ разделить на величину телесного угла, соответствующего интервалу ∆Θ:

= ЖΘ е ∆Θ) ( ) 27r∆cosΘ '

Аналогично среднюю энергию излучения, поглощенную в какой-то ча­сти поглотителя, можно найти, если при моделировании траекторий сум­мировать энергии, потерянные частицами в отдельных столкновениях в рассматриваемом объеме.

Важную роль при конструировании оценок играют формулы (45) и (46). Формула (45) говорит о том, что показания аддитивного детекто­ра представляют собой сумму вкладов отдельных столкновений, поэтому оценку сигнала можно получить по формуле

1 ^N

3=1

96 8. Моделирование траекторий частиц. Оценка характеристик...

где N - количество построенных траекторий, j - номер траектории, Qj - вклад от нее в величину 1д, который, в свою очередь, записывается в виде суммы вкладов отдельных столкновений:

%i

Q_j = ^2q(r_i,U_i,E_i,t

где fi,Qi, Е{- фазовые координаты i-й точки столкновения на j-й траекто­рии. Такой способ вычисления 1д называется оценкой по столкновениям. Например, для детектора, который подсчитывает столкновения частиц всех энергий и направлений движения, вклад от каждого столкновения равен единице, то есть q(fi,Qi,Ei,ti) = 1.

Формула (46) говорит, что сигнал детектора можно представить как сумму вкладов от отрезков пути частицы в чувствительном объеме детек­тора. На пути между двумя последовательными столкновениями энергия и направление движения не меняются и функция чувствительности D, определяемая формулой (47), постоянна, поэтому

1 ^N

3=1

г

где N - количество траекторий, j - номер траектории, U - длина i-го от­резка j-й траектории, D{ - значение функции D на этом отрезке. Такой способ вычисления 1_А называется оценкой по пробегам. Например, для де­тектора, измеряющего энергию, потерянную частицей в веществе, вклад от отрезка k равен произведению 1ф(Е{), где (3(E) - тормозная способ­ность вещества, определяемая формулой (35).

Формулу (48) для расчета показаний поверхностного детектора можно преобразовать к виду

I_s= fdtfdtt jdE jds D(r^E^) \Qfi\ <&(?,U,E,t). (57)

В соответствии с физическим смыслом дифференциальной плотности по­тока произведение \Qn\ Ф(г, Q, E,t) ds, стоящее под знаком интеграла, равно числу частиц с энергией Е и направлением движения Q, пересека­ющих в единицу времени площадку ds с нормалью it, поэтому множитель

D(f,U,E,t)

Ц-^—-— есть вклад в сигнал Is от одного пересечения. Приближенное

Qn

Вопросы

97

значение этого сигнала можно найти c помощью оценки по пересечениям:

N

N

3=1

_{«, = £ д}

i Lf v

где, как и раньше, N - количество траекторий, j - номер траектории, г - номер столкновения в j-й траектории, D{ - значение функции чувстви­тельности в точке, где частица пересекает поверхность чувствительного объема, а Q,{ и щ - направление движения частицы и нормаль к поверх­ности в этой точке.

Вопросы

132. Из каких случайных элементов состоит траектория частицы? Что нужно знать для их моделирования?

133. Как моделируется длина пробега между столкновениями?

134. Как моделируется тип взаимодействия?

135. Как моделируется угол рассеяния и энергия рассеянной частицы?

136. Как моделируется траектория частицы?

137. Опишите особенности распространения заряженных частиц в веще­стве и способы моделирования их траекторий.

138. Опишите основные способы оценки характеристик поля излучения на случайных траекториях.

Упражнения

139. Составить блок-схему и подпрограмму моделирования длины про­бега частицы до взаимодействия. Использовать ее для получения нескольких значений I.

140. Составить блок-схему и подпрограмму выборки угла рассеяния за­ряженной частицы из распределения Резерфорда с учетом экра­нирования. Использовать ее для получения нескольких значений

_{cos е.}

98 8. Моделирование траекторий частиц. Оценка характеристик...

3. Составить блок-схему и подпрограмму моделирования потери энер­ гии при рассеянии, используя модельную плотность вероятности

w(Q) = ^-^-(Е - Q) n , 0<Q<E. (58)

Использовать ее для получения нескольких значений Q.

4. Составить блок-схему и подпрограмму моделирования угла рассея­ ния кванта, используя дифференциальное сечение Томсона

^ = -(i+cos 2e). dQ 2 ^v

Использовать ее для получения нескольких значений cos в методом функции распределения и методом Неймана.

5. Составить блок-схему и подпрограмму моделирования угла выле­ та фотоэлектрона. Использовать ее для получения нескольких зна­ чений cos6 методом Неймана. Скорость фотоэлектрона выразить через энергию фотона с помощью нерелятивистского закона сохра­ нения энергии.

Задачи

141. Составить программу моделирования распределения частиц по про­бегам до взаимодействия. Привести результаты моделирования рас­пределения.

142. Составить программу моделирования распределения Резерфорда с учетом экранирования. Привести результаты моделирования угло­вого распределения.

143. Составить программу моделирования потерь энергии при рассея­нии, используя модельную плотность вероятности (58). Привести результаты моделирования распределения для нескольких значений п.

144. Составить программу моделирования угла рассеяния кванта, ис­пользуя дифференциальное сечение Томсона. Привести результаты моделирования распределения.

145. Составить программу моделирования угла вылета фотоэлектрона методом Неймана. Привести результаты моделирования распреде­ления.

Проблемы

99

6. Составить программу для расчета среднего пробега частицы до по­ глощения в среде с сечениями рассеяния и поглощения равными Σ_s и Σ_s, соответственно. Привести результаты расчета.

Указание. Для организации цикла по последовательным столк­новениям на траектории использовать функцию While.

146. Составить программу для расчета распределения частиц по длине пути до поглощения в бесконечном поглотителе с заданными сечени­ями рассеяния и поглощения. Привести результаты моделирования.

147. Составить программу для расчета распределения поглощенных ча­стиц по глубине. Сечения рассеяния и поглощения равны Σ_s и Σ_c, соответственно. Угловое распределение частиц при рассеянии счи­тать изотропным. Привести результаты моделирования.

148. Составить программу и вычислить среднюю энергию частицы, про­шедшей в веществе путь l. Считать, что потери энергии в индиви­дуальных столкновениях описываются модельной плотностью веро­ятности (58). Полное сечение взаимодействия равно Σ, поглощение отсутствует.

149. Составить программу для расчета энергетического распределения частиц, прошедших в веществе путь l. Считать, что потери энергии в индивидуальных столкновениях описываются модельной плотно­стью вероятности (58). Полное сечение взаимодействия равно Σ, по­глощение отсутствует.

150. Частицы испытывают многократное рассеяние в плоском слое веще­ства с заданными сечениями поглощения и рассеяния. Считая рас­сеяние изотропным, найти относительное количество прошедших, отраженных и поглощенных частиц.

151. Частицы испытывают многократное рассеяние в плоском слое ве­щества с заданными сечениями поглощения и рассеяния. Считая рассеяние изотропным, найти угловое распределение частиц, про­шедших через слой и отраженных от него.

Проблемы

1. Вероятностный смысл коэффициентов взаимодействия. Моделиро­вание траекторий частиц. Оценка характеристик поля излучения.

9. Статистическая погрешность метода Монте-Карло. Методы уменьшения погрешности

9.1. Статистическая погрешность метода Монте-Карло

Реальные траектории частиц в веществе и их вклады в сигнал детек­тора случайны, однако вероятностные законы, описывающие процессы пе­реноса частиц и их взаимодействия с детектором, достаточно хорошо из­вестны, и это позволяет моделировать на ЭВМ траектории, статистически эквивалентные реальным, и оценивать на них необходимые характеристи­ки радиационного поля. Важным достоинством метода Монте-Карло яв­ляется то, что он позволяет в процессе расчета находить не только среднее значение сигнала (точнее - получать оценку его математического ожида­ния), но и оценивать величину статистической погрешности результата, мерой которой является дисперсия оценки.

Напомним, что если Q - непрерывная случайная величина с плотно­стью вероятности w(Q), то ее математическое ожидание M(Q) и дис­персия D(Q) определяются формулами:

M{Q)= IQw{Q)dQ₎

D(Q) = (Q - M(Q))² w(Q) dQ = M(Q²) - (M(Q))² ,

где интегрирование ведется по всем возможным значениям Q. В дальней­шем предполагается, что M(Q) и D(Q) конечны. Указанные интеграль­ные характеристики распределения случайной величины Q обладают сле­дующими важными свойствами:

M(cQ) = c M(Q),

D(cQ) = c² D(Q),

где c - константа, и

i i

Пусть теперь Q₁, Q₂,...Q_N - случайные значения вклада в сигнал де­тектора от отдельных траекторий, наример, энергия, потерянная части­цей, или путь, пройденный ею в чувствительном объеме детектора. Пред­ставим их как случайные точки, распределенные на числовой оси вокруг

9.1. Статистическая погрешность метода Монте-Карло

101

”центральной точки” M(Q), нахождение которой и является целью вычис­лений. Мерой разброса значений Q₃ относительно M(Q) является диспер­сия D(Q).

Оценкой математического ожидания M(Q) естественно считать вели­чину

1 ^N

3=1

которая называется выборочным средним. Однако легко видеть, что каж­дая новая ”пачка” из N траекторий будет давать новое значение этой сум­мы, то есть Qn сама является случайной величиной. Ее значения распре­делены на числовой оси вокруг ”центральной точки” M(Q_N). Используя отмеченные выше свойства математического ожидания, легко показать, что

M(Q_N) = M(Q),

то есть случайные значения Qn распределены вокруг той точки, оценка которой является целью вычислений. Отклонение вычисленного значе­ния Q_N от M(Q) является статистической погрешностью расчета, мерой которой является дисперсия D(Qn).

Из отмеченных выше свойств дисперсии следует, что

D(Q_N) = -\-D(Q). (59)

Формулу (59) можно использовать для оценки статистической погреш­ности, если входящую в нее величину D(Q) выразить через вклады тра-екторй Qj. Кажется естественным, что величину D(Q) следует оценивать по формуле

D(Q)&D_N(Q),

где D_N(Q) - выборочная дисперсия, вычисляемая по формуле

1 ^N D_N(Q) = — J2(Q_J -Q_Nf.

3=1

Однако легко видеть, что выборочная дисперсия D_N(Q) - случайная ве­личина, и можно показать, что ее математическое ожидание определяется формулой

M(D_ff(0)) = ^D(Q).

Поэтому оценкой для DQ следует считать

D(Q) « j^-D_N(Q)

102 9. Статистическая погрешность метода Монте-Карло. Методы...

и оценку статистической погрешности расчета проводить по формуле

D(Qn) = j^D_N(Q).

Из этой формулы следует, что среднеквадратичная погрешность вычис­лений методом Монте-Карло медленно убывает с ростом N :

\]d{Q _n ) ~ 1/л/АГ,

то есть для уменьшения погрешности в 10 раз количество траекторий надо увеличить в 100 раз.

9.2. Методы уменьшения статистической погрешности

Из анализа, проведенного в п.9.1, следует, что статистическая по­грешность расчетов методом Монте-Карло медленно убывает с увеличе­нием количества построенных траекторий. Поэтому для увеличения эф­фективности алгоритмов разрабатываются и используются специальные методы. Некоторые из них обсуждаются ниже.

Выбор оценки. В п.8.3 описаны два основных способа вычисления характеристик поля излучения. Один из них основан на использовании оценки по столкновениям, когда сигнал детектора определяется как сум­ма вкладов от отдельных столкновений частиц. Во втором используется оценка по пробегу, когда сигнал представляет собой сумму вкладов от отрезков, из которых состоит траектория частицы. Естественно, что при­менение разных оценок для решения одной и той же задачи приведет к одному и тому же результату, однако статистические погрешности (дис­персии) оценок будут, вообще говоря, различными. Специальные иссле­дования показали, что оценка по пробегу более эффективна в тех случа­ях, когда пространственные размеры чувствительной области детектора малы. Для детекторов больших размеров более эффективна оценка по столкновениям.

Аналитическое осреднение. Для реальных частиц вклад в показа­ния детектора от столкновения или отрезка траектории обычно является случайным и может быть промоделирован на ЭВМ. Однако на практике для уменьшения статистической погрешности оценки случайное значе­ние вклада часто заменяют его средним значением. Например, если энер­гия, поглощенная в детекторе, вычисляется с использованием оценки по столкновениям, то вклад от столкновения можно находить как разность энергий частицы до и после столкновения в объеме детектора: q = Е — Е'. Это изменение энергии моделируется при построении траекторий в соот­ветствии с плотностью вероятности, которая приведена п.8.1. Но, зная

9.2. Методы уменьшения статистической погрешности

103

плотность вероятности w{E';E), можно заранее вычислить среднее зна­чение потерянной энергии

~Ё^Ш = (Е- Е') w{E'; Е) dE'

и вместо случайной разности Е — Е' использовать в качестве вклада ве­личину Е — Е'.

Аналогично при вычисления длины пути частицы в веществе до погло­щения с помощью оценки по пробегу случайный вклад от пробега между столкновениями можно находить по формуле (56). Но для уменьшения погрешности оценки вместо случайного пробега следует использовать его среднее значение, равное 1/Е.

Неаналоговое моделирование. Как указывалось в п.8.1, статисти­ческое моделирование переноса частиц в веществе заключается в построе­нии некоторого количества случайных траекторий с использованием плот­ностей вероятности, которые выражаются через сечения взаимодейстия. Эти аналоговые траектории статистически эквивалентны реальным, и их можно использовать для оценки характеристик поля излучения. При этом вклад от каждой траектории в вычисляемую величину находится в соот­ветствии с ее физическим смыслом. Такой способ вычислений называется аналоговым моделированием. Однако он неэффективен, если характери­стики поля излучения необходимо вычислить в такой области фазового пространства, где появление частицы является маловероятным. Приме­ром может быть вычисление энергетического коэффициента отражения для заряженных частиц, который равен отношению суммарной энергии частиц, отраженных слоем вещества, к энергии падающих частиц. Выше указывалось, что заряженные частицы рассеиваются преимущественно на малые углы, и поэтому количество отраженных частиц невелико. В этом случае для получения результата с необходимой точностью потребовалось бы построить очень большое количество траекторий.

Для преодоления указанной трудности используют неаналоговое мо­делирование, заключающееся в том, что для моделирования элементов траектории используются плотности вероятности, отличные от реальных. Они искусственно подбираются таким образом, чтобы обеспечить более частое появление частиц в интересующей нас области пространства. В упомянутом примере с вычислением энергетического коэффициента от­ражения для моделирования угла рассеяния вместо вытянутого вперед распределения, соответствующего формуле Резерфорда, берут изотроп­ное распределение, искусственно увеличивая тем самым количество ча­стиц, рассеянных на большие углы. Полученные таким образом неана­логовые траектории, естественно, не будут статистически эквивалентны реальным, и чтобы использовать их для получения результата решаемой

104 9. Статистическая погрешность метода Монте-Карло. Методы...

задачи, вклад от каждой траектории должен быть изменен таким обра­зом, чтобы среднее значение интересующей нас характеристики радиа­ционного поля, вычисленное на неаналоговых траекториях с новой фор­мулой для вклада, было равно среднему значению, которое получается при аналоговом моделировании. В обсуждаемом примере с коэффициен­том отражения заряженных частиц вклад от каждой неаналоговой тра­ектории (он равен случайному значению энергии отраженной частицы) надо уменьшить во столько раз, во сколько раз увеличивается количе­ство отраженных частиц при переходе от аналогового моделирования к неаналоговому.

Модифицированную формулу для вычисления вклада, которую на­до использовать при неаналоговом моделировании, получим на примере, рассмотренном в п.4.1. Там было показано, что приближенное значение

интеграла

ь

1= If(x)w{x)dx (60)

а

можно найти статистическим моделированием по формуле

1 ^N

N

i =—^ /м, (61)

где случайные числа x_i получены выборкой из распределения w(x), ко­торое будем считать ”аналоговым”, то есть соответствующим некоторой физической задаче. Если подынтегральное выражение в (60) умножить и разделить на ”неаналоговую” плотность вероятности w˜(x):

ь / = -^-f{x)w{x) dx,

a

то формула для оценки интеграла примет вид, аналогичный (61):

1 ^N I

У w^f(x)

где числа x_i получаются выборкой из неаналоговой плотности w˜(x).

Такое преобразование, очевидно, не меняет величины I, но соответ­ствующая оценка имеет другую дисперсию. При удачом выборе функции w˜(x) величина статистической погрешности модифицированной оценки может быть значительно меньше, чем при использовании формулы (61).

9.2. Методы уменьшения статистической погрешности

105

Приведенные формулы показывают, что при переходе от аналогового моделирования случайных точек x_i к неаналоговому меняется формула для вычисления величины вклада в интеграл от каждой из этих точек. Вклад при неаналоговом моделировании отличается от вклада при ана­логовом моделировании множителем

w(x)

W(x)

W{X)

который равен отношению аналоговой плотности, соответствующей физи­ческой задаче, к неаналоговой. Этот множитель называется статисти­ческим весом.

Такой же результат получается и при неаналоговом моделировании процесса переноса. Для неаналогового моделирования каждой траекто­рии используются специально подобранные выражения для плотностей вероятностей ее случайных элементов. Таким элементом может быть дли­на пробега, тип взаимодействия, угол рассеяния и т.д. Формулы для рас­пределений этих элементов выбираются таким образом, чтобы искусствен­но увеличить количество ”ценных” траекторий, попадающих в нужную нам область фазового пространства. При этом вклад от каждого столк­новения, вычисленный по ”аналоговым ” формулам, умножается на ста­тистический вес траектории, который равен единице в начале траектории и изменяется после розыгрыша каждого случайного элемента:

W_n+l = W

ⁿw(x)

где w{x) и w (х) - аналоговое и неаналоговое распределения случайного элемента траектории.

Статистический вес можно рассматривать как дополнительную фазо­вую координату частицы, которая меняется вдоль траектории так же, как ее пространственные координаты, энергия, направление движения.

Рассмотрим несколько примеров.

В п.8.1 отмечалось, что при аналоговом моделировании типа взаимо­действия рассеяние происходит с вероятностью p_s = —^. В сильно погло­щающих веществах, где p_s близко к 0, количество частиц быстро убывает с глубиной, и получить надежные данные о потоке излучения за защитой большой толщины весьма трудно. Одним из приемов, который использу­ют в этом случае, является замена аналоговой вероятности выживания p_s на неаналоговую p_s = 1. То есть тип взаимодействия не разыгрывает­ся, и считается, что частица всегда рассеивается. Отсутствие поглощения, очевидно, увеличит количество частиц на большой глубине. Чтобы ском­пенсировать это увеличение и получить правильную величину потока,

106 9. Статистическая погрешность метода Монте-Карло. Методы...

статистический вес частицы после каждого столкновения умножается на

Ps

отношение — = p_S) что уменьшает вклад от этой траектории.

Ps

При аналоговом моделировании переноса частиц пробег между столк­новениями разыгрывают по формуле (56). В расчетах защит большой тол­щины среднюю длину пробега иногда искусственно увеличивают для того, чтобы увеличить количество траекторий, проходящих защиту. Это мож­но сделать, уменьшив в формуле для моделирования величину сечения Е. Такую замену компенсируют при вычислении вкладов, умножая ста­тистический вес частицы после каждого розыгрыша пробега на множи­тель, равный отношению плотностей вероятности (23), соответствующих сечениям ЕиЕ.

В качестве модифицированного сечения иногда берут

£ = £-с cos6,

где с - подбираемый множитель. В этом случае особенно большими будут пробеги частиц, летящих под малыми углами, что существенно увеличит количество частиц на больших глубинах.

Определенные сложности возникают и при расчете поля рассеянного излучения в очень тонком поглотителе, где столкновения происходят ред­ко, потому что частицы с большой вероятностью пролетают его без взаи­модействия. В этом случае для увеличения эффективности расчетов так­же модифицируют моделирование длины пробега. Пробег разыгрывают из распределения, отличающегося от (23) нормировочным множителем. Он берется таким, чтобы длина пробега была ограничена максимальным значением, которое равно расстоянию от точки столкновения до границы поглотителя вдоль направления движения. Изменение плотности вероят­ности, используемой для моделирования, компенсируется статистическим весом.

Для того, чтобы бороться с уменьшением потока частиц, обусловлен­ным их поглощением, можно использовать еще один прием, который за­ключается в том, что после каждого рассеяния, если оно произошло в ”ценной” для нас области пространства, траектория расщепляется. То есть из точки, где произошло рассеяние, строится не одна, а несколько траекторий. Для того, чтобы оценка вычисляемой характеристики при этом осталась несмещенной, статистический вес каждой ветви умножает­ся на 1/к, где к - кратность расщепления.

Траекторию можно расщеплять не в точке столкновения, а при пере­сечении границы интересующей нас области.

Эффективность расчетов повышают не только увеличивая количество траекторий в некоторой области пространства, но и обрывая их при попа­дании туда, откуда переход в ценную область маловероятен. В этом слу-

Вопросы

107

чае при каждом столкновении траектории обрываются с вероятностью г,

а вес оставшихся умножается на . Этот прием называется русской

рулеткой.

Вопросы

152. Перечислите основные свойства математического ожидания и дис­персии.

153. Объясните смысл терминов ”выборочное среднее” и ”выборочная дисперсия”. Чему равны математические ожидания этих величин?

154. Как оценивается статистическая погрешность в расчетах методом Монте-Карло? Как она зависит от количества построенных траек­торий?

155. Перечислите основные оценки характеристик радиационных полей. Как влияет выбор оценки на результаты расчетов?

156. Сформулируйте основную идею и приведите примеры использова­ния аналитического осреднения.

157. Объясните, что значит ”неаналоговое моделирование”. Поясните на примерах, когда оно используется.

158. Объясните, как вычисляется вклад от траектории при неаналоговом моделировании.

159. Приведите примеры задач, где целесообразно использовать неана­логовое моделирование.

Упражнения

1. На примере равномерно распределенных случайных чисел убеди­тесь в том, что выборочное среднее и выборочная дисперсия явля­ются случайными величинами.

Задачи

1. Составить программу и провести расчет распределения случайной

1А

величины х и распределения нормированной суммы у = — Х{

п ^

108 9. Статистическая погрешность метода Монте-Карло. Методы...

при нескольких значениях n (на примере равномерного и экспонен­циального распределений).

160. Составить программы и вычислить среднее значение пути части­цы до поглощения, используя оценку по пробегу и соответствующее аналитическое осреднение. Сравнить дисперсии оценок.

161. Составить программы и вычислить средние потери энергии части­цы, прошедшей путь l, используя оценку по столкновениям и соот­ветствующее аналитическое осреднение. Считать, что потери энер­гии в индивидуальных столкновениях описываются модельной плот­ностью вероятности (58). Сравнить дисперсии оценок.

162. Частицы испытывают многократное рассеяние в плоском слое веще­ства с заданными сечениями поглощения и рассеяния. Считая рассе­яние изотропным, вычислить коэффициенты отражения и прозрач­ности слоя аналоговым моделированием и учитывая поглощение с помощью статистических весов. Сравнить дисперсии оценок.

Проблемы

1. Cтатистическая погрешность метода Монте-Карло. Методы умень­шения статистической погрешности.

10. Расчет переходных и граничных эффектов

Рис. 44. Плотность распределения поглощенной энергии в воде.

Важным достоинством метода Монте-Карло является то, что он поз­воляет вести расчеты радиационных полей с учетом реальной геометрии системы источник-поглотитель-детектор. В таких задачах при пересече­нии границы раздела двух сред траектория должна строиться с коэф­фициентами взаимодействия, соответствующими той зоне системы, куда попала частица. Расчеты показывают, что такие характеристики радиаци­онного поля, как плотность потока частиц, интенсивность излучения, рас­пределение поглощенной энергии, резко меняются вблизи границы раз­дела сред, отличающихся по своим свойствам. Это изменение называется переходным эффектом. Такие задачи часто встречаются в физике защиты от излучений, радиационной медицине, радиационной физике и технике.

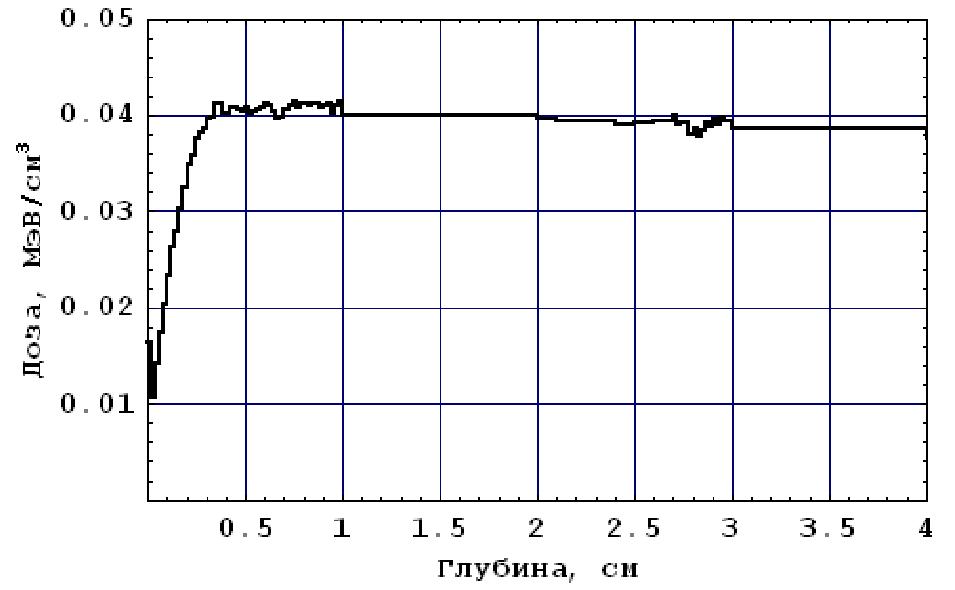
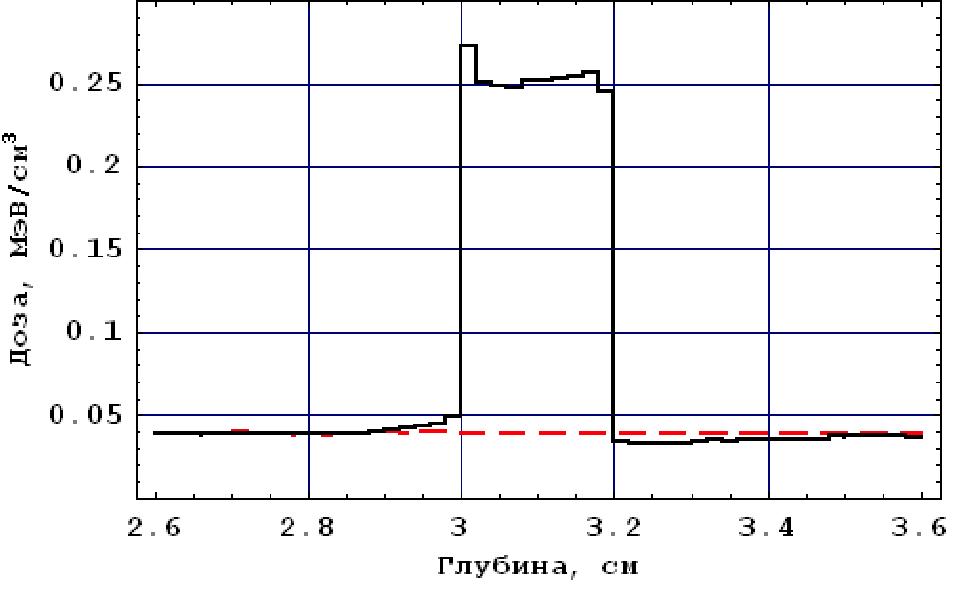
Рис. 45. Плотность распределения поглощенной энергии в воде и трех­слойном поглотителе вода-металл-вода. Пунктир - доза в воде.

Для примера на рис.44 и 45 приведены результаты расчета плотно­сти распределения поглощенной энергии гамма-излучения от источника Co⁶⁰ (E_γ = 1.25 МэВ) в воде и трехслойном поглотителе вода-металл

110

10. Расчет переходных и граничных эффектов

(ЖГг)-вода. Такая комбинация имитирует металлический протез в теле пациента при лучевой терапии. Из рис.45 видно, что поглощенная энергия увеличивается перед слоем металла и уменьшается - за ним. Увеличение дозы перед металлом обусловлено двумя причинами. Во-первых, вторич­ные электроны, которые рождаются квантами в воде перед слоем метал­ла, частично отражаются от него. Во-вторых, электроны, рожденные в металле, испытывают многократное рассеяние и могут вылететь из слоя в обратном направлении. Все это приводит к увеличению обратного тока перед металлом и, следовательно, к увеличению дозы. Уменьшение дозы за металлом вызвано тем, что вторичные электроны из воды не прохо­дят через металл, так как их пробег меньше толщины слоя, а количество электронов, рожденных в металле и летящих вперед, меньше, чем летело в воде, из-за большего рассеяния в веществе с большим Z. Уменьшение прямого тока за слоем приводит к уменьшению дозы.

Этот пример наглядно иллюстрирует возможности метода Монте-Карло, который позволяет не только рассчитать эффект (возмущение дозного по­ля слоем металла), но и выяснить его причину - характер изменения токов вторичных электронов.

Поле излучения резко меняется не только в неоднородном поглотите­ле у границ раздела сред, но и у границ пучка, распространяющегося в однородной среде. На рис.46 приведено радиальное распределение погло­щенной энергии в воде от коллимированного пучка гамма-излучения ис­точника Со⁶⁰ на различных глубинах от облучаемой поверхности. Рис.46 демонстрирует уменьшение дозы вблизи границ пучка, вызванное утеч­кой квантов из этой области. Этот эффект особенно заметен для сильно

коллимированных пучков.

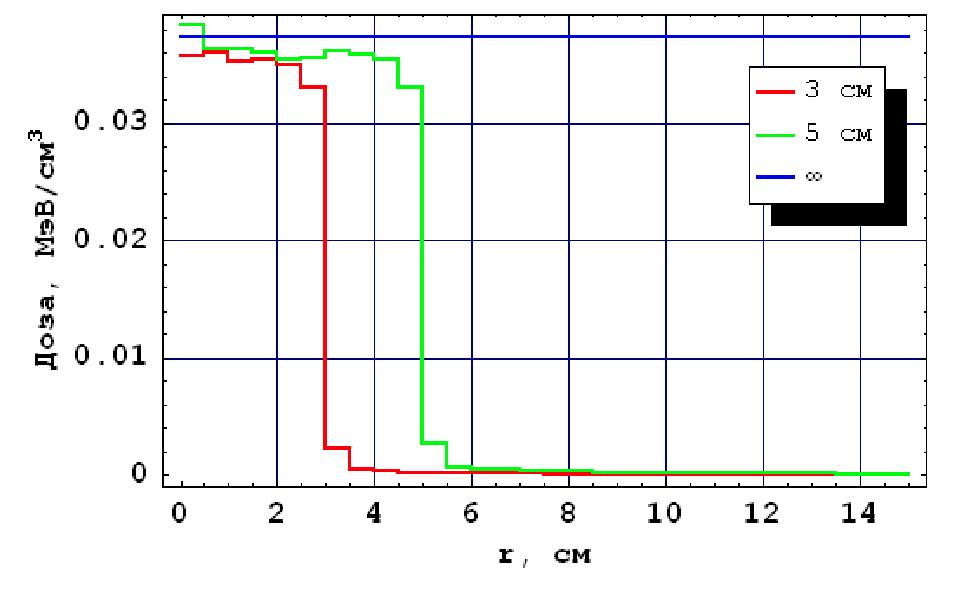
Рис. 46. Радиальное распределение поглощенной энергии в воде от колли­мированного пучка 7-излучения источника Со⁶⁰ на различных глубинах от облучаемой поверхности. Радиус пучка R=3 см, 5 см, оо.

На рис.47 показана зависимость дозы на оси пучка от глубины при различных значениях радиуса поля облучения. Из рисунка видно, что на

10. Расчет переходных и граничных эффектов

Ill

оси сильно коллимированного пучка доза убывает с глубиной по закону, близкому к экспоненциальному. Это значит, что после однократного рас­сеяния гамма-кванты вылетают из области прямой видимости источника и не возвращаются в нее в результате следующих столкновений. Следова­тельно, в этой области не происходит накопления многократно рассеянно­го излучения, как это имеет место при распространении широких пучков. То есть узкий пучок гамма-излучения, распространяясь в веществе, не уширяется в результате рассеяния, что является важным достоинством при его практическом использовании.

Рис. 47. Зависимость дозы на оси пучка от глубины при различных зна­чениях радиуса поля облучения.

112

Приложение

Приложение

Компьютерное моделирование случайного явления заключается в ге­нерации последовательностей случайных чисел, статистически эквива­лентных тем, которые получаются в реальном эксперименте, многократно повторенном в одних и тех же условиях.

Пример 1. Эксперимент с многократным подбрасыванием монеты дает последовательность чисел к = 0 (”орел”) и к = 1 (”решка”) с веро­ятностями Р(0) = Р(1) = 1/2. При статистичеcком моделировании такие числа можно получать по формуле

к = [2₇],

где 7 - случайные числа, равномерно распределенные в интервале (0,1), а символ [q] означает целую часть числа q.

Пример 2. Равновероятные числа к = 1,2...6, получающиеся при подбрасывании игрального кубика, можно моделировать по формуле

к = [б₇] + 1.

Пример 3. Случайное число к, равное количеству подбрасываний монеты до первого появления ”орла”, можно получить с помощью блок-схемы и листинга подпрограммы, приведенных на рис.48.

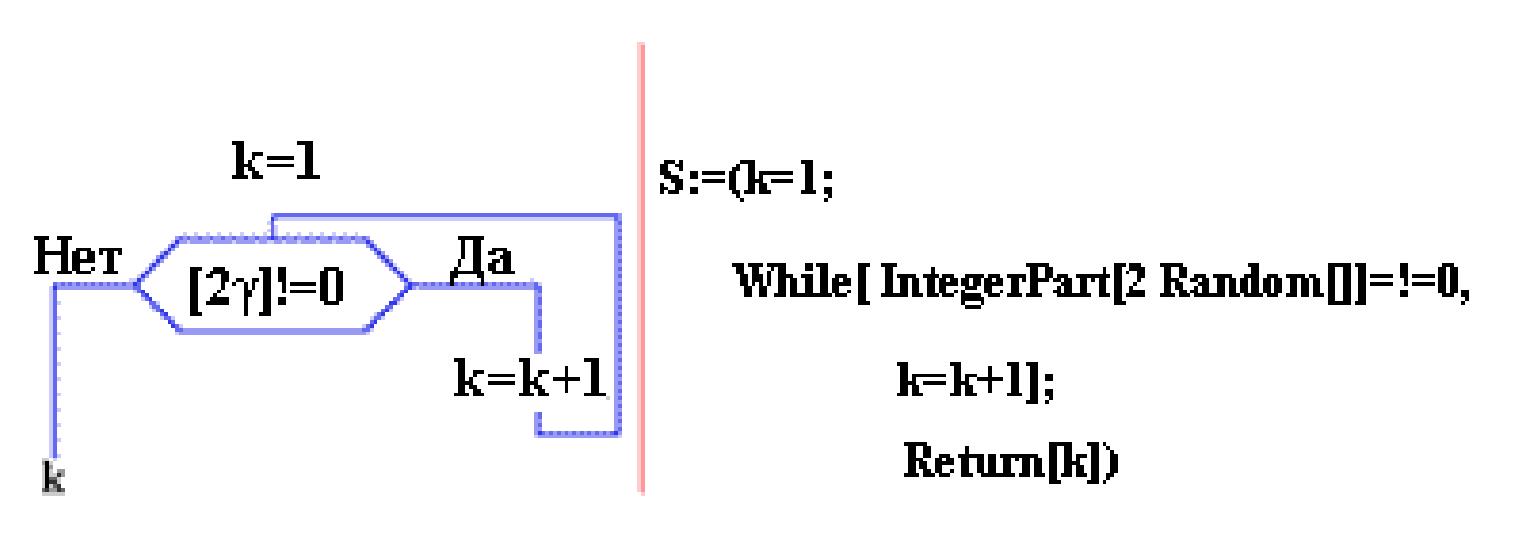
Рис. 48. Блок-схема и листинг подпрограммы моделирования подбрасы­вания монеты до первого ”орла”.

Пример 4. Если отрезок (0,1), на котором откладываются равно­мерно распределенные числа 7? разделен на неравные отрезки, длины которых равны вероятностям Р_к, то номер интервала к (к = 1,2...), в который попадает очередное значение 7, можно найти с помощью блок-схемы и листинга подпрограммы, приведенных на рис.49.

Здесь д - рабочая ячейка для хранения случайного числа 7, R - ра­бочая ячейка для вычисления суммы вероятностей Р_к, Р[к_]- шаблон вычисления вероятностей.

Приложение

113

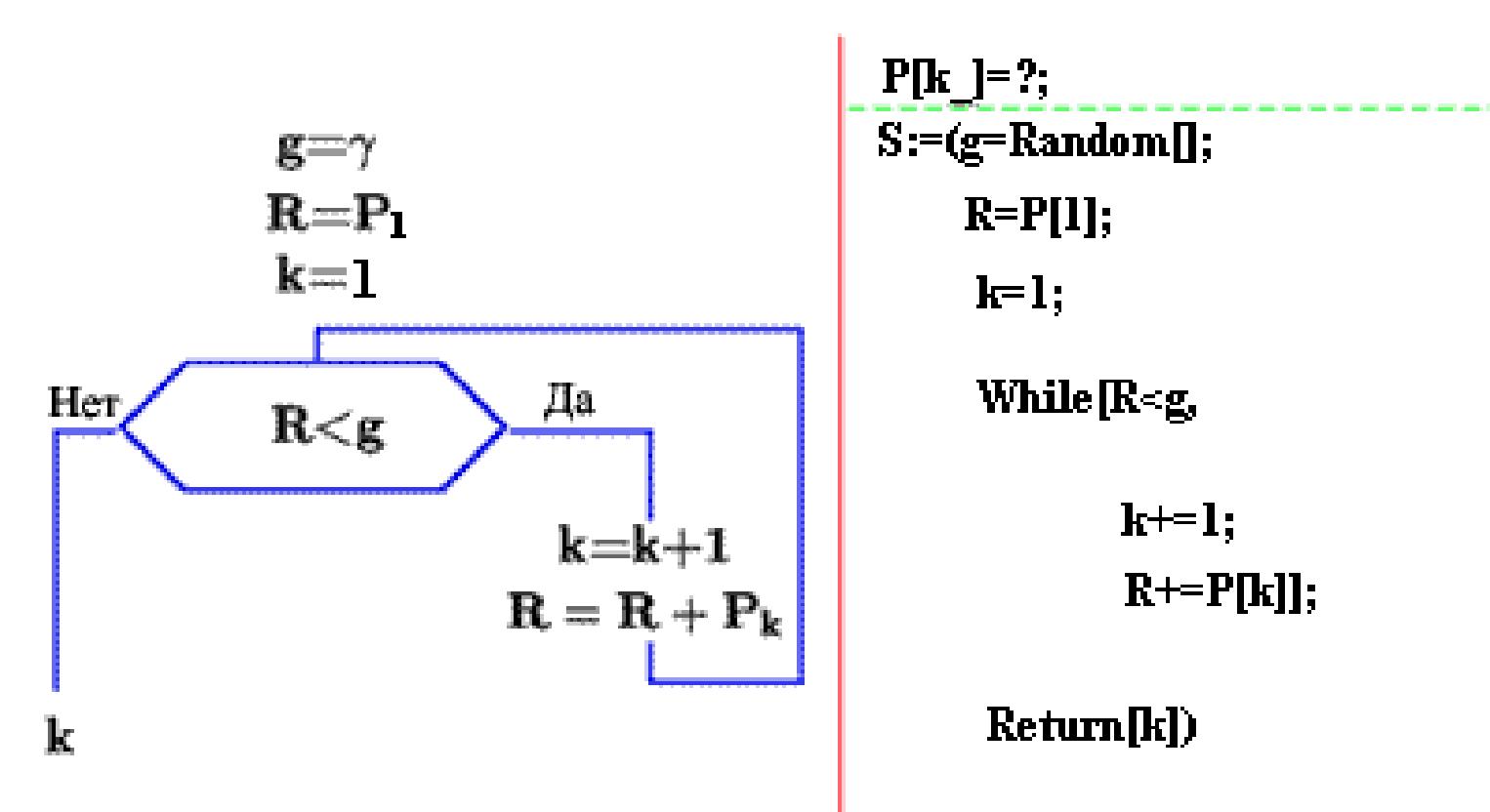
Рис. 49. Блок-схема и листинг подпрограммы нахождения номера интер­вала к из распределения Р_к.

Для моделирования чисел к из распределения Р_к с помощью рекур­рентной формулы (10) можно использовать блок-схему и листинг подпро­граммы, приведенные на рис.50.

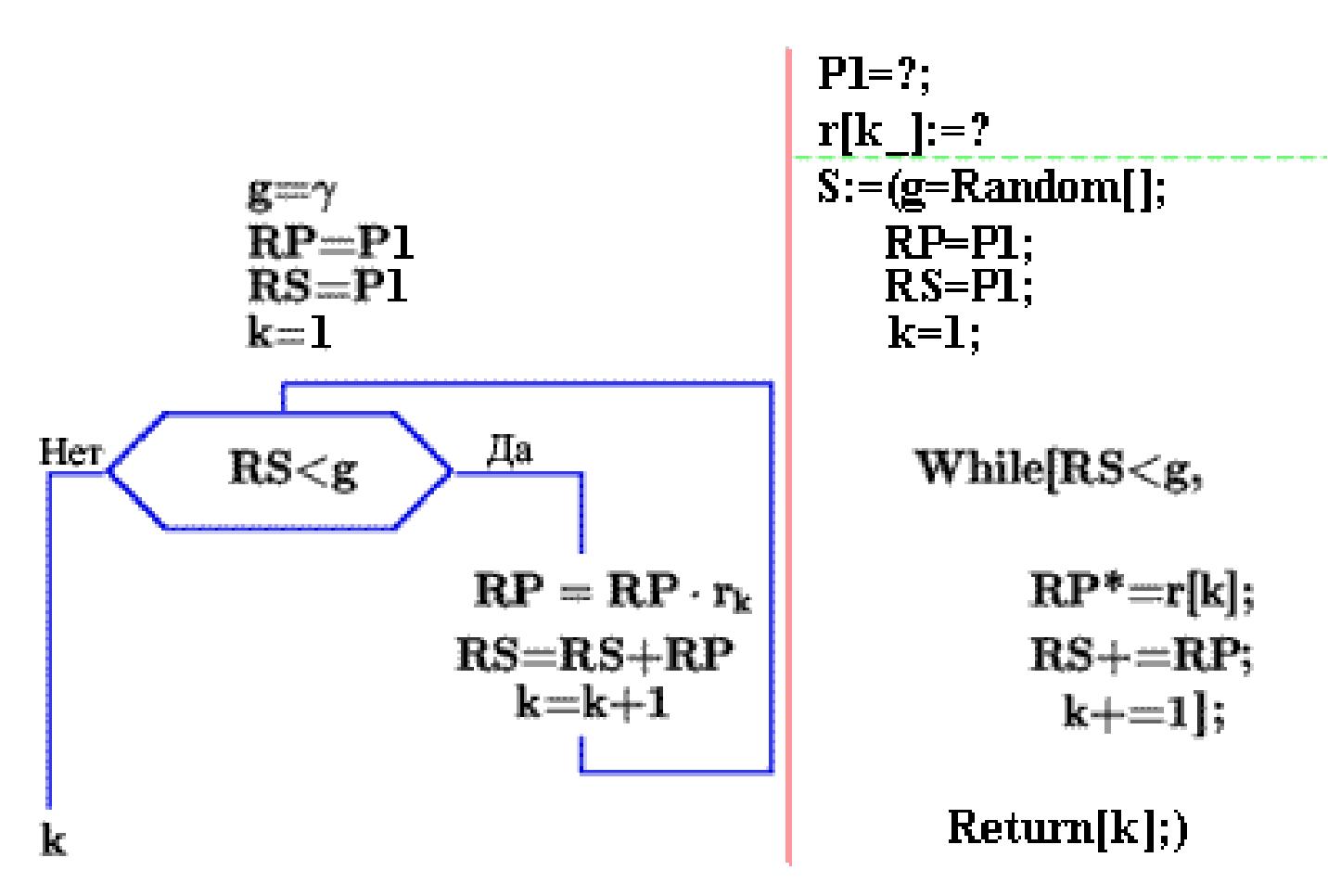
Рис. 50. Блок-схема и листинг подпрограммы моделирования номера ин­тервала к из распределения Р_к с помощью рекуррентной формулы.

Здесь д - рабочая ячейка для хранения случайного числа 7, RP - ра­бочая ячейка для вычисления вероятностей Р_к по рекуррентной формуле, RS - рабочая ячейка для вычисления суммы вероятностей , г[к_] - шаб­лон для вычисления множителя рекуррентной формулы.

Наиболее часто встречающиеся задачи статистического моделирова-

114

Приложение

ния можно разделить на 3 группы.

1. Требуется получить N_t случайных чисел x и вывести их на печать. Блок-схема и листинг программы VIEW, которые решают эту задачу, приведены на рис.51.

Рис. 51. Блок-схема и листинг программы VIEW.

Здесь Т - массив получаемых значений х_к, к = 1, 2, ..N_h а оператор S представляет собой либо формулу для вычисления х по случайному значению 7, которая подобна тем, что приведены в Примерах 1, 2, либо подпрограмму со структурой, как в Примерах 3, 4.

Для того, чтобы записать случайные числа, генерируемые подпро­граммой S, в виде таблицы и показать их на графике, программу VIEW следует дополнить командами

ТаЫе[{к,Т[[к]]}, {к, Nt}]//MatrixForm

Tp = Table[{T[[k}],0},{k,Nt}}; ListPlot[Tp].

(62)

Если подпрограмма S генерирует координаты {х, у} случайных точек на плоскости или {х₎ у₎ z} в трехмерном пространстве, то команда (62) за­меняется на

Tp = Table[T[[k]],{k,Nt}];

2. Требуется получить N_t случайных чисел х и вычислить среднее значение

1

N_t

2_\^Хк-

к=1

ОС ——

Блок-схема и листинг программы AVERAGE, которые решают эту задачу, приведены на рис.52.

Приложение

115

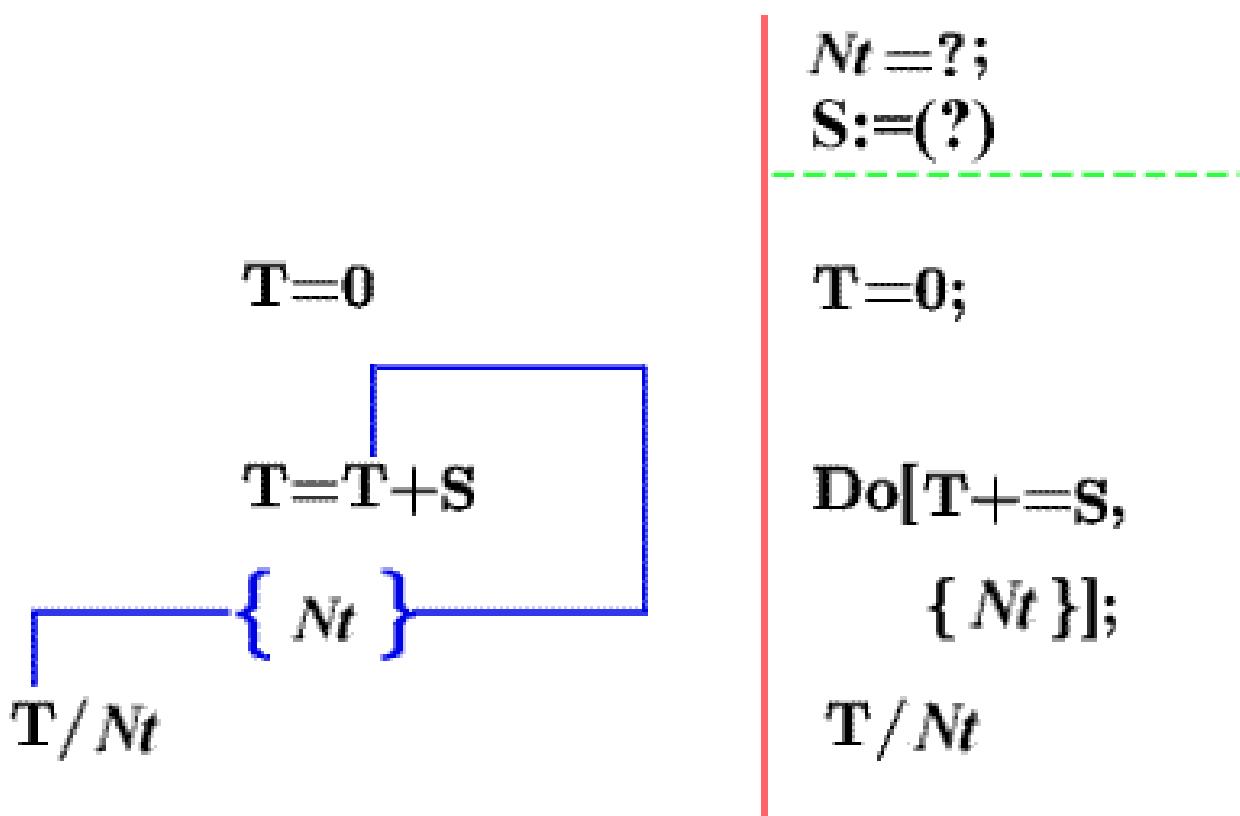
Рис. 52. Блок-схема и листинг программы AVERAGE.

Здесь Т - рабочая ячейка для вычисления суммы, S- подпрограмма моделирования случайного числа х.

3. Требуется найти распределение значений случайной величины.

3.1. Если набор {х_к}, к = 1,2,...п возможных значений случайной величины х дискретен и конечен, то оценка вероятности любого х_к из этого набора проводится по формуле

_Рк „ N(x = х_к)

Рис. 53. Блок-схема и листинг программы D-DISTRIBUTION.

где N{x = Xk) - число, показывающее, сколько раз значение х = х_к встретилось в серии из N_t испытаний. Блок-схема и листинг программы D-DISTRIBUTION, которые решают эту задачу, приведены на рис.53.

116

Приложение

Здесь Т - массив для вероятностей Р_к) к = 1, 2, ...n, S - подпрограмма моделирования случайного числа к.

Если количество возможных значений величины х бесконечно, то опе­ратор цикла на рис.53 дополняется сравнением к < п:

Do[S; If [к <= п,Т[[к}}+ = 1], {Ж}}.

При этом вычисляются n первых величин Р_к.

Представить массив вероятностей Р_к в виде таблицы и построить гра­фик распределения можно, дополнив программу, приведенную на рис.53, командами

« Graphics¹ Graphics¹

Table[{k,T[[k]]},{k,n}}/ /MatrixForm

Тр = ТаЫе[{к,Т[[к]],0.2},{к,п}];

GeneralizedBarChart[Tp].

3.2. Если случайная величина х пробегает непрерывный ряд значений

а < х < Ь, то для нахождения соответствующей плотности вероятности

w(x) область (а, Ь) разбивается на малые интервалы Ах и для каждо-

N(x е Ах) го интервала находится величина —— , которая является оценкой

плотности вероятности. Здесь N(x G Ах) - число, показывающее, сколько раз значение х G Ах встретилось в серии из N_t испытаний.

Если отрезок (а, Ь), на котором откладываются случайные числа х,

разделен на п равных частей Ах = , то номер интервала к, в кото-

п рый попадает очередное значение ж, находится по формуле

_гх — а,

^{к = hsri+ L}

Блок-схема и листинг программы C-DISTRIBUTION, которые реша­ют задачу моделирования непрерывного распределения, приведены на рис.54.

Здесь Т - массив для значений плотности вероятности w(xk), к = 1, 2, ...п в интервалах Ах_к, S - подпрограмма моделирования случайного числа х.

Если область значений величины х бесконечна, то оператор цикла на рис.54 дополняется сравнением а < х <Ь:

Do[S; If[And[x >=а,х<=Ъ],к = IntegerPart[^—^} + 1;

T[[k]]+ = l],{Nt}].

Приложение

117

Рис. 54. Блок-схема и листинг программы С-DISTRIBUTION.

При этом плотность вероятности w(x) вычисляется в интервале (a, b).

Представить массив T в виде матрицы и построить график плотности вероятности можно, дополнив программу, приведенную на рис.54, коман­дами

<< Graphics‘Graphics‘

ТаЫе[{а + — (2k 2

l),T[[k]]},{k,n}]//MatrixForm

Тр

ТаЫе[{а + —(2к 2

l),T[[k]],dx},{k,n}];

GeneralizedBarChart[Tp].

Если подпрограмма S генерирует координаты случайных точек {х, у} на плоскости то их распределение в области —а < х < а, —а < у < а можно построить с помощью программы, обобщающей C-DISTRIBUTION на случай двух измерений:

« Graphics¹GraphicsZD¹

Nt=?; а =?; п =?; dx = 2а/щ

S :=(?); Т = Та&/е[0,{г,71},О>}];

Do[S;If[And[Abs[x] < a,Abs[y] < а],

_к

dx

IntegerPart[^] + 1;

118

Приложение

JntegerPart^] + _i;

T[[k,l]]+ = l],{Nt}];

ВагС/шг£3£[Т].

Литература

119

^{Основная литература}

163. Соболь И.М. Численные методы Монте-Карло. - М.: Наука, 1973.

164. Кольчужкин А.М., Учайкин В.В. Введение в теорию столкновений. - Изд. ТГУ. Томск, 1979.

165. Кольчужкин А.М., Учайкин В.В. Введение в теорию прохождения частиц через вещество. - М.: Атомиздат, 1978.

166. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. - М.: Наука, 1988.

167. Дьяконов В. Mathematica 4: учебный курс. - Спб.: Питер, 2001.

168. Метод статистических испытаний. Под ред. Ю.А.Шрейдера.- М.: ГИФМЛ, 1962.

^{Дополнительная литература}

169. Аккерман А. Ф. Моделирование траекторий заряженных частиц в веществе. - М.: Энергоатомиздат, 1991.

170. Балашов В.В. Строение вещества. - М.: Изд. МГУ, 1993.

171. Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая элек­тродинамика. - М.: Наука, Физ.мат.лит., 1989.

172. Войтишек А.В. Основы метода Монте-Карло в алгоритмах и зада­чах, 1-5. - Новосибирск: Изд. НГУ, 1997, 1999.

173. Гмурман В.Е. Теория вероятностей и математическая статистика. -М.: Высшая школа, 1977.

174. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию веро­ятностей. - М.: ”Наука”, 1976.

175. Гольданский В.И., Куценко А.В., Подгорецкий М.И. Статистика от­счетов при регистрации ядерных частиц. - М.: ГИФМЛ, 1959.

176. Гулд X., Тобочник Я. Компьютерное моделирование в физике, ч.1,2. - М.: Мир, 1990.

177. Джексон Дж. Классическая электродинамика. - М.: Мир, 1965.

120

Литература

178. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. - М.: Наука, 1982.

179. Машкович В.П., Кудрявцева А.В. Защита от ионизирующих излу­чений. Справочник. - М.: Энергоатомиздат, 1995.

180. Михайлов Г.А. Некоторые вопросы теории методов Монте-Карло. -Новосибирск: Наука (Сиб. отделение), 1974.

181. Поляченко А.Л. Численные методы в ядерной геофизике. - М.: Энер-гоатомиздат, 1987.

182. Ремизович В.С., Рогозкин Д.Б., Рязанов М.И. Флуктуации пробегов заряженных частиц. - М.: Энергоатомиздат, 1988.

183. Тормозная способность электронов и позитронов. Доклад 37 МКРЕ. / Под ред. И.Б.Керим-Маркуса. - М.: Энергоатомиздат, 1987.

184. Хастингс Н., Пикок Дж. Справочник по статистическим распреде­лениям. - М.: Статистика, 1980.

185. Chilton A., Shultis J., Faw R. Principles of Radiation Shielding. - Prentice-Hall Inc., Englewood Cliffs, New Jersey, 1984.