3. Случайные точки в многомерном пространстве

3.1. Случайные точки, равномерно распределенные на плоскости и в пространстве

Случайные точки, равномерно распределенные в прямоугольнике {Ъ— а) х h на плоскости хОу, можно получить, моделируя ж-координату точ­ки из равномерного распределения на (а, 6), а у-координату - из рав­номерного распределения на (0, К) (величины а, Ь, и h предполагаются конечными). Легко догадаться, что случайные числа ж, равномерно рас­пределенные в интервале (а, 6), можно получить из чисел 7, равномерно распределенных в (0,1), по формуле

_ж = _а+(6-а)₇. Числа, равномерно распределенные в (0, h), получаются по формуле

Получение случайных точек на плоскости с помощью ЭВМ можно считать, например, моделированием следов от капель дождя на дороге или космических частиц, падающих на поверхность Земли. Результаты такого моделирования приведены на рис. 7.

Рис. 7. Случайные точки на плоскости.

Случайные точки, равномерно распределенные в параллелепипеде боль­шего числа измерений, можно получить, моделируя из равномерного рас­пределения каждую координату этих точек.

3.2. Вычисление площадей и объемов. Вычисление определенных интегралов методом Монте-Карло

Случайные точки, равномерно распределенные в круге радиуса R, можно получить, моделируя их координаты х и у равномерно в (—R,R) и оставляя только те пары, для которых

х² + у² < R².

Легко видеть, что отношение полного числа полученных точек к числу точек, оказавшихся внутри круга, приближенно равно отношению пло­щадей квадрата и круга. То же самое справедливо для любой плоской фигуры и охватывающего ее прямоугольника, поэтому указанным мето­дом можно моделировать случайные точки, равномерно распределенные в произвольной плоской области, а ее площадь S_m вычислять по формуле

S_in = S^, (11)

где S— площадь прямоугольника, N{_n— количество случайных точек, по­павших в область Si_n, N— количество точек в прямоугольнике. Отноше­ние -jj- характеризует эффективность использования случайных чисел.

Для круга, вписанного в квадрат, S = 4R², и Si_n = nR², поэтому формулу (11) можно преобразовать к виду

N in

7Г = 4

N

и использовать для статистического вычисления числа 7Г. Результаты вы­числений приведены на рис.8. Из рисунка видно, что с увеличением коли­чества случайных точек отличие статистической оценки от точного зна­чения уменьшается.

Аналогичным образом получаются случайные точки, равномерно рас­пределенные в произвольной области пространства более высокой раз­мерности. Для этого случайными точками заполняют параллелепипед со­ответствующей размерности и оставляют те из них, которые оказались внутри рассматриваемой области. Этот метод используется, например, для моделирования пространственных координат точек, где происходит распад атомов радиоактивного вещества и рождаются быстрые частицы, траектории которых затем строятся методами статистического моделиро­вания.

Отношение ^ равно отношению объемов рассматриваемой области

и параллелепипеда и может быть использовано для вычисления объема тела или области сложной формы.

24

3. Случайные точки в многомерном пространстве

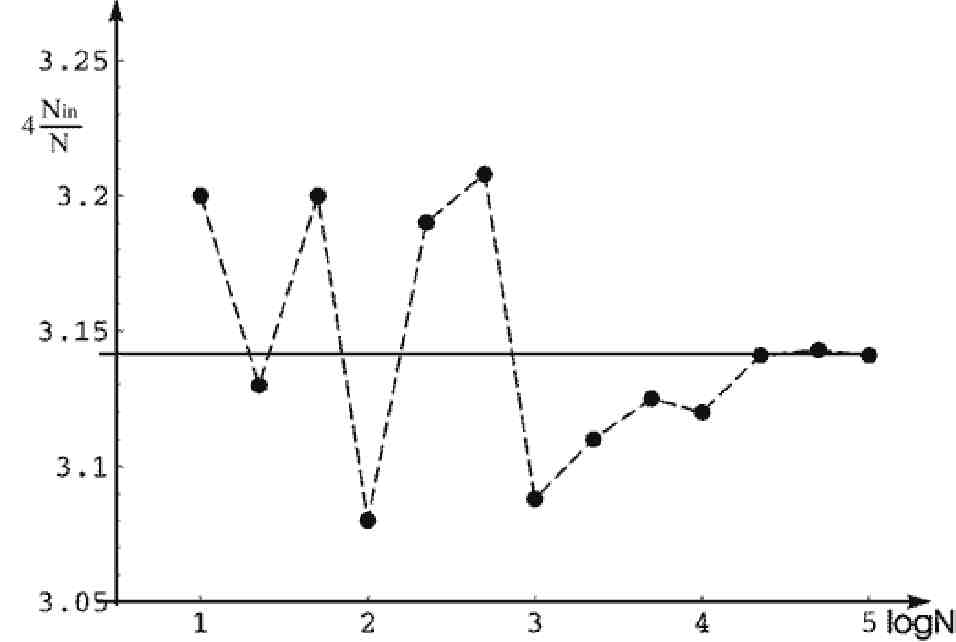
Рис. 8. Результаты вычисления числа 7Г статистическим моделированием.

Следует отметить, что отбрасывание точек, оказавшихся вне выделен­ной области, вообще говоря, приводит к тому, что координаты оставшихся точек будут распределены неравномерно. На рис.9 приведена плотность вероятности ж—координат случайных точек, равномерно распределенных в круге. Легко видеть, что количество отброшенных точек велико, если \х\ ~ R, поэтому плотность вероятности оставшихся точек там меньше.

Рис. 9. Плотность вероятности ж—координат случайных точек, равномер­но распределенных в круге.

Вычисление массы, положения центра инерции и момента инерции тела. Для системы материальных точек с массами т«, распо­ложенных в точках с координатами г,, масса, положение центра инерции R и величина момента инерции / относительно точки ?о определяются формулами:

М = ^т_г, (12)

I

R

_£

^тгГг

_м

тлп-го,

(13) (14)

3.2. Вычисление площадей и объемов. Вычисление определенных... 25

Будем считать, что все точки имеют одинаковую массу т и равномер­но заполняют объем V_in трехмерного пространства. Через V обозначим объем параллелепипеда, охватывающего V_in и заполненного точками с той же плотностью , что и V_in. Через N и N{_n обозначим количество точек в V и Vi_n, соответственно. Тогда, учитывая, что mNi_n = М, а

mN

где р— средняя плотность вещества в системе, формулы (12)-(14) можно записать в виде

м = V_P f,

1Ъ

^{1 = УрПЩ_А}

2

где fi_n— радиусы-векторы точек, находящихся в V_in-

Рис. 10. К расчету массы, положения центра инерции и момента инерции однородного тела.

Эти формулы можно использовать для вычисления массы, положения центра инерции и момента инерции однородного тела заданной формы методом статистического моделирования. Для этого величины, стоящие в правых частях формул, находят, заполняя объем параллелепипеда слу­чайными точками равномерно и учитывая те из них, которые оказались внутри V_in (см. рис.10).

Вычисление определенных интегралов методом Монте-Карло.

Если в прямоугольник (Ь — а) х h вписать кривую f(x) (рис.11) и запол­нить его равномерно распределенными точками, то отношение количества

26