12 1. Введение. Статистическая эквивалентность и моделирование

Вопросы

25. Приведите примеры явлений с устойчивым и случайным исходами.

26. Опишите статистически устойчивую часть в придуманных вами при­мерах.

27. Проиллюстрируйте примерами понятия ”вероятность” и ”плотность вероятности”.

28. Придумайте примеры, иллюстрирующие основные вероятностные законы для дискретных и непрерывных случайных величин.

29. Объясните, что означает термин ”статистическое моделирование слу­чайных событий”.

2. Равномерно распределенные случайные числа

2.1. Генерация равномерно распределенных случайных чисел

Важную роль в процессах статистического моделирования играют случайные числа, равномерно распределенные в интервале (0,1). Извест­но, что их можно получать из трансцендентных чисел, таких, например, как тг = 3.141 592 653 ..., ”разрезанием” мантиссы этого числа на части, содержащие определенное количество цифр, если каждую из них считать мантиссой очередного случайного числа: 0.141, 0.592, 0.653,.... В микрокалькуляторах последовательность равномерно распре­деленных чисел 7 часто получают с помощью рекуррентной формулы

_7г+1 = М(37_7г),

где символ М(х) означает мантиссу числа х. Программы, встроенные в ЭВМ, используют близкую идею. В пакете Mathematica равномерно рас­пределенные случайные числа получают с помощью функции Random [ ]. Эти числа, конечно, не являются случайными в прямом смысле этого слова, так как получены по определенному алгоритму, однако в практи­ческих расчетах они работают как ”настоящие” случайные числа. Их на­зывают псевдослучайными. Их статистическая устойчивость проявляется в том, что любая достаточно длинная серия этих чисел покрывает от­резок (0,1) ”ровным слоем”. Равномерность распределения означает, что плотность вероятности для них не зависит от х: w(x) = С . Численное значение константы С находится интегрированием этого равенства с уче­том условия нормировки (2), откуда следует, что С = 1.

На рис.1 показано распределение случайных чисел 7 в интервале (0,1). Плотность вероятности вычислялась по формуле

^У ) N Ах '

где N(x е Ах) - количество случайных точек, попавших в Ах.

Из рисунка видно, что случайные отклонения от равномерности умень­шаются с увеличением N.

Моделирование подбрасывания монеты, игрального кубика, жеребьевки. Многократное подбрасывание ”честной” монеты генериру­ет последовательность случайных чисел 0 (орел) и 1 (решка), которые равновероятны. Статистически эквивалентную последовательность нулей

14

2. Равномерно распределенные случайные числа

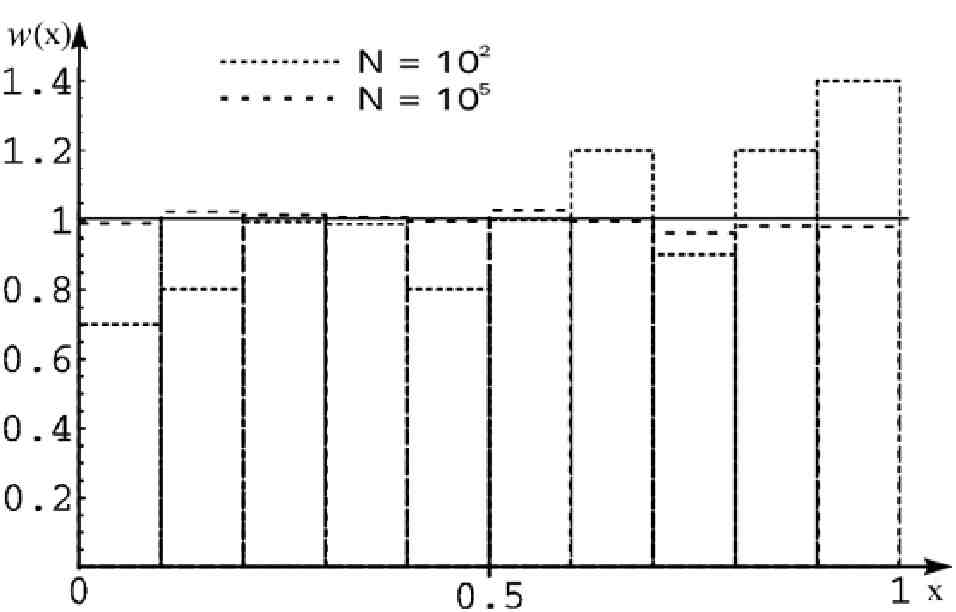
Рис. 1. Плотность вероятности для случайных чисел, равномерно распре­деленных в (0,1).

и единиц можно получить на компьютере, если генерировать случайные числа 7, равномерно распределенные в интервале (0,1), и записывать 0, если 7 < 0.5, и 1, если 7 > 0.5. Результаты такого моделирования пред­ставлены на рис.2.

в ч

^ Р(О)

\

\ -о- о" -е„

> =

У р(1)

/ --•'

5 logN

Рис. 2. Результаты моделирования подбрасывания монеты.

Из рисунка видно, что с увеличением числа испытаний N отношения N("0")/N и N("1")/N стремятся к одному и тому же предельному зна­чению, равному 1/2.

Для моделирования подбрасывания ”честного” игрального кубика ин­тервал (0,1) делится на 6 равных частей, и номер интервала, в который попадает очередное случайное число 7, принимается за число очков, вы­павшее на кубике.

Для моделирования жеребьевки, определяющей одного победителя из п участников, интервал (0,1) делится на п равных частей, и такое мо­делирование напоминает картину азартной игры с помощью рулетки в казино.

Описанный метод легко обобщается и может быть использован для решения задач, где вероятности Pk случайных исходов А^ не равны друг

2.1. Генерация равномерно распределенных случайных чисел 15

другу. В этом случае отрезок (0,1) должен быть разделен на части, длины которых равны соответствующим вероятностям Р&. Попадание случайно­го числа 7 в интервал с номером к означает реализацию события А^. В практических задачах часто встречаются следующие распределе-

ния.

Биномиальное распределение, где количество интервалов конечно:

Рк

п\ к\(п-к)\

р^к(1-р)^п-\ 0<р< 1, fc = 0,l,2,...n,

(7)

n и p - параметры распределения. Количество интервалов, на которые разбивается отрезок (0,1), здесь равно n +1. Вид распределения показан на рис.3. Положение максимума распределения определяется величиной параметра p. С увеличением p максимум смещается вправо.

0.45

0.4 0.35

0.3 0.25

0.2 0.15

0.1 0.05

					-А	р=0.35, п=5
			}	г		р-0.55, п-5
J	.-"	\	V	\
/ /			/	\
/	/ /	/	\	1	Г
/	/	- 1	к	\ \
L ,	/	/	\
/	/	к	\	\
г . и	*■			"^	l

1

2 3 4 5

к

6

7

S

Рис. 3. Биномиальное распределение.

Биномиальное распределение (7) определяет вероятность того, что в серии из n независимых испытаний событие А, которое происходит с ве­роятностью p и не происходит с вероятностью 1 - p, встретится k раз. Возможные значения случайной величины k равны 0, 1, ...n.

Геометрическое распределение:

P_k =p(1-p)^k-1, 0<p<1, k=1,2,...∞, (8)

p - параметр распределения. Здесь количество интервалов бесконечно. Вид распределения приведен на рис.4. С увеличением параметра p функ­ция P_k убывает быстрее.

Геометрическое распределение (8) определяет вероятность того, что случайное событие А, которое происходит с вероятностью p и не происхо­дит с вероятностью 1 - p, в первый раз произойдет при k-ом испытании.

Распределение Пуассона, где число интервалов тоже бесконечно:

Рк

_к\

e"^m, fc = 0,l,2,...oo,

(9)

16

2. Равномерно распределенные случайные числа

2

ю

0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

Г

\

-■ р=0.55

\\

+ Р=0.75

\_

г >

^

~^w

'^S^^^

It- it J

9

3

4

7

X

5 6

к

Рис. 4. Геометрическое распределение.

m - параметр распределения. При m ≤ 1 функция P_k монотонно убывает с ростом k. Если m > 1, то распределение имеет максимум, который смещается вправо с увеличением m (рис.5).

0.6

0.5

0.4

0.3

0.2

0.1

L
Г							m=2.0 1
\						-*■	m=5.0 1
\ \						"■
/ \	'
i \	Ж *	-,	K+
	V	\ i A			i-^.		L-. . -*_ . . . . -

0

2

4

6 8

к

10

12

14

Рис. 5. Распределение Пуассона.

Примеры задач, где случайная величина имеет распределение Пуас­сона, приводятся ниже.

При статистическом моделировании распределений (7)-(9) их удобно записывать в виде рекуррентных соотношений

P_k+1 =r_kP_k , задавая отдельными формулами выражения для P₁ и r_k.

(10)

Моделирование процессов размножения. Рассмотрим популя­цию, состоящую из т живых организмов. Каждый из них произведет за свою жизнь случайное количество потомков к (к = 0,1,2,...). Ес­ли вероятность произвести к потомков известна, то развитие популяции можно моделировать. Моделирование заключается в том, что вероятно­сти Pk откладываются на отрезке (0,1), а затем для каждого организма генерируется случайное число 7 и по нему находится номер интервала, в

2.1. Генерация равномерно распределенных случайных чисел 17

который попадает это число. Номер интервала принимается за случайное количество потомков кг (г = 1,2, ...т) данного организма. Сумма

N

_J2k*

i=i

дает количество организмов в следующем поколении. Повторяя эту проце­дуру мы получаем данные о дальнейшем развитии популяции. При этом номер поколения играет роль времени.

Примеры случайной функции ЛГ(п), показывающей количество орга­низмов в п—ом поколении, приведены на рис.6. Расчеты проведены в предположении, что количество потомков одного организма случайно и имеет пуассоновское распределение (9).

N(n)
70 60		k=1.22
50
40
30
20 10		k=0.43

10

2 4 6 8

П

Рис. 6. Зависимость количества организмов в популяции от номера поко­ления.

Две кривых на рисунке соответствуют двум значениям параметра m, определяющего среднее количество потомков от одного организма:

оо

к = ^ к Р_к = т.

к=0

При к > 1 количество организмов в популяции в среднем растет, а при к<1- убывает.

Аналогичные задачи встречаются и в других областях, например, в физике при исследовании размножения нейтронов в ядерном реакторе.

18 2. Равномерно распределенные случайные числа

Вопросы

30. Опишите алгоритмы моделирования равномерно распределенных случайных чисел в интервале (0, 1).

31. Опишите алгоритм моделирования простейших случайных событий: подбрасывания монеты или кубика, жеребьевки среди нескольких участников.

32. Опишите алгоритм моделирования неравновероятных случайных со­бытий.

33. Назовите основные дискретные распределения и приведите приме­ры случайных явлений, которые описываются этими распределени­ями.

34. Опишите вероятностные характеристики процесса размножения жи­вых организмов и алгоритм моделирования эволюции популяции по поколениям.

Упражнения

35. Получить и показать графически несколько равномерно распреде­ленных случайных чисел.

36. Записать формулу, моделирующую подбрасывание кубика. Исполь­зовать ее для получения нескольких значений k (k = 1, 2, ...6).

37. Составить блок-схему и подпрограмму для моделирования подбра­сывания двух кубиков и подсчета суммарного количества очков. По­лучить несколько значений суммы.

38. Составить блок-схему и подпрограмму для моделирования подбра­сывания кубика и подсчета количества подбрасываний до первого появления грани с 6-ю очками. Привести результаты моделирова­ния.

39. Проверить нормировку и вычислить среднее значение для основных дискретных распределений (7)-(9).

40. Составить таблицу и построить график биномиального распределе­ния, используя программу

P[k_] :=?;

Задачи

19

p=?; n=?;

Table[{k, Р[к}}, {к, О, п}]//MatrixForm;

Т_р = ТаЫе[{к, РМ, 0.2}, {к, О, п}];

« Graphics‘Graphics‘;

GeneralizedBarChart[T_p],

где Р[к_] - шаблон вычисления вероятности, соответствующий фор­муле (7).

41. То же для геометрического распределения.

42. Записать рекуррентную формулу (10), составить блок-схемы и под­программы моделирования номера интервала к, в который попадает равномерно распределенное в интервале (0,1) число 7, для бино­миального и геометрического распределений. Привести результаты моделирования к.

Задачи

43. С помощью программы C-DISTRIBUTION продемонстрировать рав­номерность случайных чисел, генерируемых функцией Random[ ].

44. Составить программы моделирования подбрасывания двух кубиков и подсчета суммарного количества очков

• для оценки среднего значения суммы,

• для оценки вероятности каждого возможного значения.

Сравнить результаты моделирования при нескольких значениях N.

3. Составить программы моделирования подбрасывания игрального кубика до первого появления грани с 6-ю очками

• для оценки среднего количества подбрасываний,

• для оценки вероятности Р& того, что это произойдет при к—ом подбрасывании.

Привести и обсудить результаты моделирования.

4. Составить программы моделирования случайной величины, кото­ рая может принимать значения Xk с вероятностями Р&, заданными рекуррентной формулой (10)

20

2. Равномерно распределенные случайные числа

l А

• для оценки среднего значения х = — ^х_к,

к=\

для оценки вероятностей P_k.

Привести результаты моделирования для биномиального и геомет­рического распределений. Сравнить результаты моделирования с даннными, полученными в Упражнениях 6, 7, используя функцию Show[].

Исследовать зависимость величины х от параметров распределений.

5. Построить случайную кривую эволюции популяции, используя про­ грамму

Ng=?;

S={?);

T = Table[0,{Ng}];

г = 1;

Г[[1]] =?;

Do[Do[T[[i + 1]]+ = S, {Т[[г]]}]; г+ = l,{i,Ng- 1}];

ListPlot[T],

где Ng - число поколений, Т - массив, в который записывается ко­личество организмов в поколениях l,2...Ng, Т[[1]] - количество ор­ганизмов в первом поколении, а S - подпрограмма, моделирующая случайное количество потомков от одного организма. Считая, что число потомков подчиняется биномиальному распределению, полу­чить кривые эволюции при нескольких значениях параметров п,р, определяющих среднее количество потомков одного организма.

45. В каждом шоколадном яйце спрятан один из п различных новогод­них призов. Cоставить программу и вычислить среднее количество шоколадных яиц, которые необходимо купить, чтобы собрать пол­ную коллекцию призов.

46. Составить программу и вычислить вероятности Р_к в предыдущей задаче, где к - количество шоколадных яиц, которые необходимо купить, чтобы собрать все возможные призы.

47. Составить программу и провести моделирование игры в ”орлянку”. Оценить

Проблемы

21

• среднюю продолжительность игры до разорения одного из иг­роков,

• вероятности разорения каждого игрока.

Исследовать зависимость этих величин от начального капитала иг­роков Q₁ и Q₂.

Проблемы

1. Устойчивость, случайность, статистическая устойчивость, статисти­ческое моделирование. Моделирование простейших случайных явле­ний.