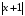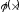ИПР 2 ТВиМС
.docxГруппа 792351
Быкович Екатерина
Индивидуальная практическая работа №2
Вариант 1
Задача 5.1
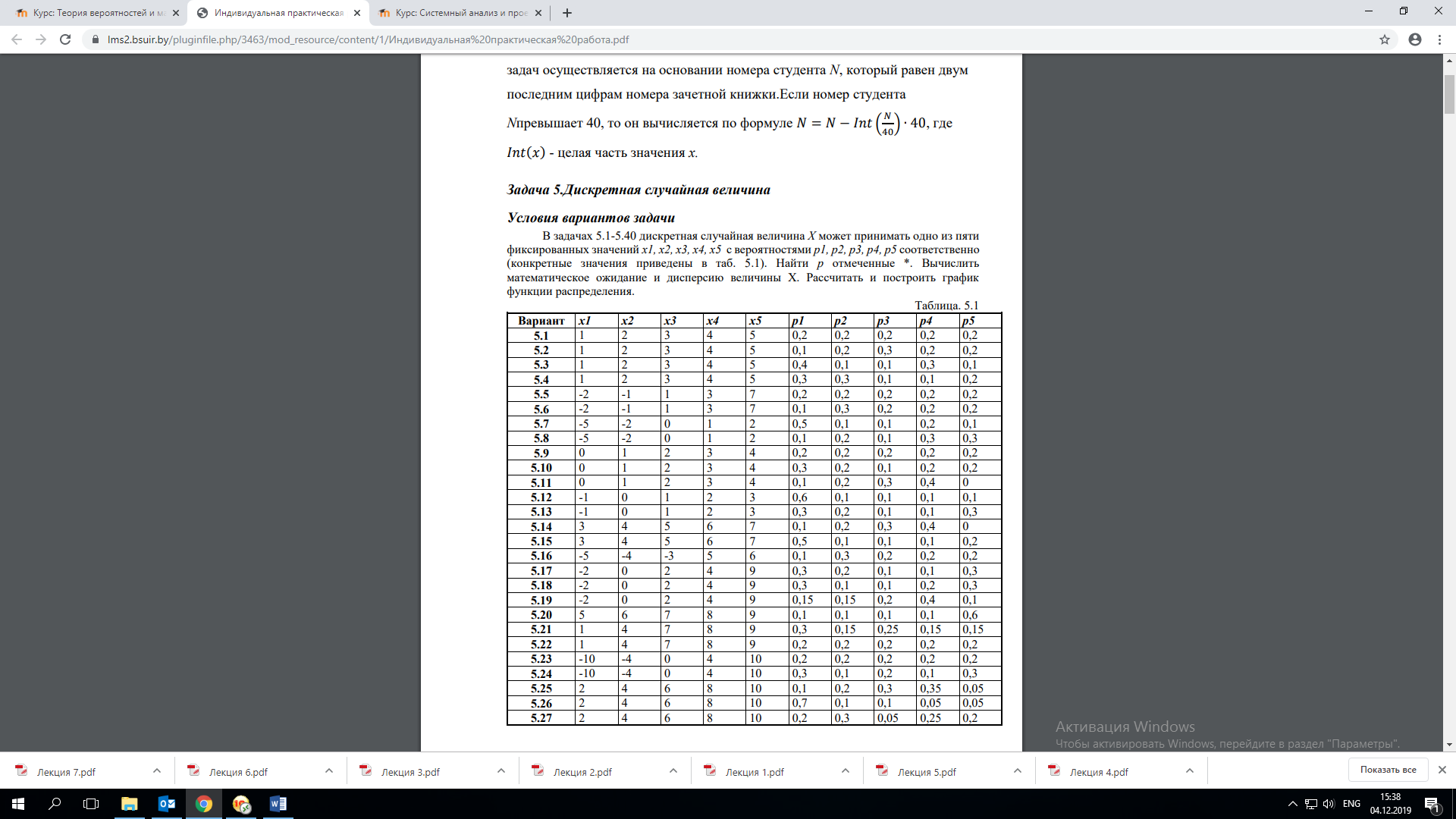
Рассчитаем значения функции распределения для фиксированных значений Х=хi, взятых из ряда распределения:
-

-
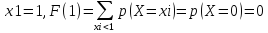
-
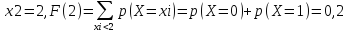
-
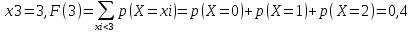
-
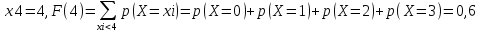
-

-
При х>6 функции распределения F(x)=1.
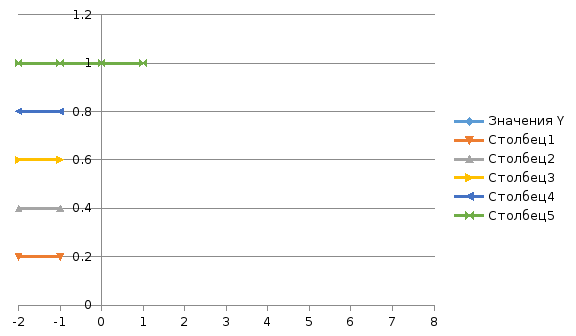
График функции распределения F(x)
Опишем построение графика функции распределения F(x). Рассмотрим первый промежуток по оси Х от -∞ до 1, согласно пункту 1 и 2 значение F(x)=0 и линия идет по оси Х до 1 включительно (при значении Х<0 функция распределения F(x)=0). Второй промежуток по оси Х от 1 до 2; согласно пункту 3 значение F(x)=0,2, значит проводим ступеньку высотой 0,2. Третий промежуток по оси Х от 2 до 3; согласно пункту 4 значение F(x)=0,4, значит проводим ступеньку высотой 0,4. Четвертый промежуток по оси Х от 3 до 4; согласно пункту 5 значение F(x)=0,6, значит проводим ступеньку высотой 0,6. Пятый промежуток по оси Х от 4 до 5; согласно пункту 6 значение F(x)=0,8, значит проводим ступеньку высотой 0,8. Шестой промежуток по оси Х от 5 до 6; согласно пункту 7 значение F(x)=1, значит, проводим ступеньку высотой 1. При значении Х>6 функция распределения F(x)=1.
Математическое ожидание дискретной СВ Х определим по формуле:
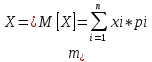
M[X] =1*0,2+2*0,2+3*0,2+4*0,2+5*0,2=3
Дисперсию дискретной СВ Х определим по формуле:
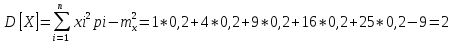
Задание 6.1
Случайная величина Х задана плотностью вероятности

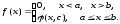
Определить
константу С,
математическое ожидание, дисперсию,
функцию распределения величины Х,
а также вероятность ее попадания в
интервал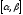 .
.
|
Вариант |
|
a |
b |
|
|
|
6.1 |
c |
-3 |
3 |
-0,5 |
1,5 |
Вначале вычислим значение константы с из условия нормировки. Условие нормировки представляет собой интегральное уравнение, из которого можно определить неизвестный параметр плотности вероятности. Для этого определим значение интеграла в левой части условия нормировки:
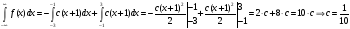
Плотность вероятности примет вид:
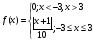 Математическое
ожидание найдём по формуле:
Математическое
ожидание найдём по формуле:
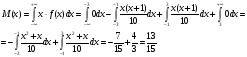
Дисперсию найдём по формуле:
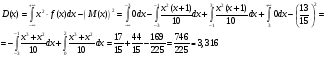
Найдём функцию распределения:
Так как плотность вероятности задана различными формулами на разных интервалах, то и ее первообразную - функцию распределения будем искать для каждого интервала в отдельности.
Для:

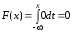
Для
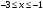
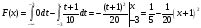
Для
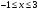
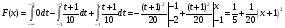
Для
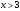
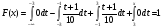
Получаем:
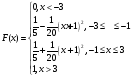
Вычислим вероятность:

Задание 7.1
Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
|
Вариант |
|
a |
b |
|
7.1 |
|
-1 |
4 |
Построим
график функции
 на
промежутке [-1;4]:
на
промежутке [-1;4]:
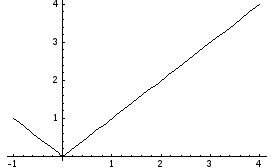
Так как X равномерно распределена на [-1;4], то её плотность вероятности равна:
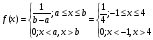
Плотность вероятности g(y) величины Y определяется по формуле:

где
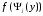 - плотность
вероятности Х,
- плотность
вероятности Х,
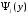 -
функция,
обратная Y,
-
функция,
обратная Y,
к – число обратных функций для Y.
В зависимости от числа обратных функций выделим следующие интервалы:
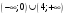 к=0
к=0
 к=1
к=1
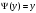
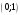 к=2
к=2
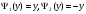
Таким
образом, на
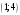 имеем:
имеем:
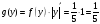
на
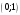 имеем:
имеем:
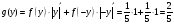
Окончательно,
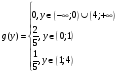

 x,c)
x,c)