Контрольная работа №2
.docxМинистерство образования Республики Беларусь
Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Факультет инновационного непрерывного образования
Кафедра экономической информатики
КОНТРОЛЬНАЯ РАБОТА №2
по дисциплине
«Основы дискретной математики и теория алгоритмов»
Выполнил: студент группы 792351
Быкович Екатерина Ивановна
Преподаватель___________________
Дата____________________________
МИНСК 2019
5.1.
Найти методом Квайна-МакКласски
минимальную ДНФ функции, заданной своим
характеристическим множеством
|
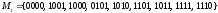
x1 |
x2 |
x3 |
x4 |
f |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
СНДФ=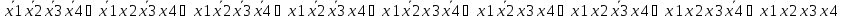
|
0 |
0000* |
-000 |
|
1
|
1000*
|
10-0 100-
|
|
2
|
1010 1001 0101
|
101- 1-10 10-1 1-01 -101 |
|
3 |
1011 1101 1110 |
1-11 11-1 111-
|
|
4 |
1111 |
|
|
|
0000 |
1001 |
1000 |
0101 |
1010 |
1101 |
1011 |
1111 |
1110 |
|
p1 |
-000 |
1 |
|
1 |
|
|
|
|
|
|
|
p2 |
10-0 |
|
|
1 |
|
1 |
|
|
|
|
|
p3 |
100- |
|
1 |
1 |
|
|
|
|
|
|
|
p4 |
101- |
|
|
|
|
1 |
|
1 |
|
|
|
p5 |
1-10 |
|
|
|
|
1 |
|
|
|
1 |
|
p6 |
10-1 |
|
1 |
|
|
|
|
1 |
|
|
|
p7 |
1-01 |
|
1 |
|
|
|
1 |
|
|
|
|
p8 |
-101 |
|
|
|
1 |
|
1 |
|
|
|
|
p9 |
1-11 |
|
|
|
|
|
|
1 |
1 |
|
|
p10 |
11-1 |
|
|
|
|
|
1 |
|
1 |
|
|
p11 |
111- |
|
|
|
|
|
|
|
1 |
1 |
|
vpi |
|
p1 |
p3 v p6 v p7 |
p1 v p2v p3 |
p8 |
p2 v p4vp5 |
p7 v p8vp10 |
p4vp6vp9 |
p9vp10vp11 |
p5vp1 |
ДНФ(минимальная)=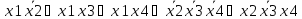
6.1. Найти инварианты графа, заданного матрицей смежности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
1 |
1 |
1 |
|
1 |
|
2 |
1 |
|
1 |
|
|
1 |
|
3 |
1 |
1 |
|
1 |
1 |
1 |
|
4 |
1 |
|
1 |
|
|
1 |
|
5 |
|
|
1 |
|
|
1 |
|
6 |
1 |
1 |
1 |
1 |
1 |
|
Существуют следующие инварианты графов
-
Количество вершин n=6
-
Количество ребер r=11
-
Количество граней f=2-n+r=7
-
Число связности k=1 (кол-во связных подграфов данного графа)
-
Толщина графа t(G)=1, т.к. данный граф является плоским (его можно уложить на плоскости)
-
Плотность графа q(G)=3 (кол-во вершин max клики графа)
-
Число независимости
Вершина с наименьшей степенью – х5 (r(х5)=2), включим ее в независимое множество. Удалим из графа вершину х5, смежные с ней вершины х3 и х6 и инцидентные им ребра х3 х1, х3 х2, х3 х4, х3 х5, х3 х6, х5 х6, х6 х1, х6 х2, х6 х4. В итоге получим граф вида:
Выбираем х2 с Г(х2)=1 и включаем ее в искомое множество, а число удаления смежных вершин и инцидентных им ребер в оставшуюся вершину х4. Наибольшее независимое подмножество {х5, х2, х4} и, соответственно, число независимости графа = 3.
-
Число вершинного покрытия
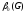
Строим матрицу инцидентности графа:
|
|
х1х2 |
х1х3 |
х1х4 |
х1х6 |
х2х3 |
х2х6 |
х3х4 |
х3х5 |
х3х6 |
х4х6 |
х5х6 |
|
х1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
х2 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
х3 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
х4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
х5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
х6 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Столбец с min единиц (х1,х2) покрывает строки х1 и х2. Среди них строки с max единиц - х1. Включаем ее в искомое покрытие . Их матрицы исключаем строку х1 и столбцы, которые она покрывает:
|
|
х2х3 |
х2х6 |
х3х4 |
х3х5 |
х3х6 |
х4х6 |
х5х6 |
|
х2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
х3 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
х4 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
х5 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
х6 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Их матрицы исключаем строку х3 и столбцы, которые она покрывает:
|
|
х2х6 |
х4х6 |
х5х6 |
|
х2 |
1 |
0 |
0 |
|
х4 |
0 |
1 |
0 |
|
х5 |
0 |
0 |
1 |
|
х6 |
1 |
1 |
1 |
Удалению
из матрицы подлежит строка х6 и все
остальные столбцы. Значит, наименьшее
вершинное покрытие {х1, х3, х6} и
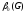=3.
+
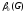=6=n
(Лемма 1 выполнена)
-
Число паросочетания
.
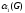Ребро с min степенью х1х2 – исключили и включили в паросочет. Также исключаем смежные ему ребра х1х3, х1х4, х1х6, х2х3, х2х6.
Ребро с min степенью х4х3 – исключили и включили в паросочетание
Искомое покрытие :{ х1х2, х3х4, х5х6}
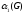=3
-
Число реберного покрытия
.
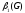Из
Леммы 2
+
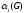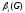=n,
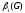=6-3=3
-
Число доминирования
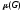
Построим матрицу смежности и дополним ее единицами по главной диагонали:
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
х 1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
х2 |
1 |
1 |
1 |
0 |
0 |
1 |
|
х3 |
1 |
1 |
1 |
1 |
1 |
1 |
|
х4 |
1 |
0 |
1 |
1 |
0 |
1 |
|
х5 |
0 |
0 |
1 |
0 |
1 |
1 |
|
х6 |
1 |
1 |
1 |
1 |
1 |
1 |
Строка с max единиц – х3 – вводим в покрытие. Вычеркиваем строку х3и покрываемые ею столбцы.
Доминирующее
множество вершин: {x3}
и число доминирования
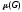=1
-
Хроматическое число
|
|
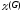
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
степень |
4 |
3 |
5 |
3 |
2 |
5 |
|
|
х3 |
х6 |
х1 |
х2 |
х4 |
х5 |
|
цвета |
1 |
2 |
3 |
4 |
4 |
3 |
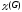=4
-
Реберно-хроматическое число
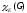
р(х) – max степень вершины графа
р(х)=5
р(х)
≤
≤
р(х)
+ 1
5≤
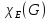≤6
Раскраска
5 цветами возможна =>
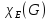=5
-
Коцикломатическое число
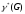
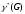=n-1=6-1=5
(число ребер в остовном дереве)
Остовное дерево (если добавим хоть одно ребро, получил цикл, т.е. это будет уже не остовное дерево)
-
Цикломатическое число
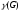
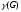=r-2+1=11-6+1=6
(число ребер, которые необходимо удалить
из графа, чтобы получить остовное
дерево).