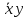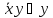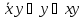Контрольная работа №1

Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет информатики и радиоэлектроники»

Факультет инновационного непрерывного образования

Кафедра экономической информатики

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине

«Основы дискретной математики и теория алгоритмов»

Выполнил: студент группы 792351

Быкович Екатерина Ивановна

Преподаватель___________________

Дата____________________________

МИНСК 2019

1. Используя диаграммы Эйлера-Венна, решить задачу.

Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике, астрономии. Три спецкурса посещают 10 студентов, по математике и фи­зике - 30, по математике и астрономии - 25; спецкурс только по физике - 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике - 145, по аст­рономии - 100 студентов. Сколько студентов посещают спец­курс только по астрономии? Сколько студентов посещают два спецкурса?

Решение

В качестве универсального выберем множество всех деталей. Число его элементов равно 500. Пусть А - множество студентов, посещающих спецкурс по математике, В – по физике, С – по астрономии. Число элементов множества А обозначим n(A). Оно равно 345, т.е. n(A)=345. Аналогично, n(В)=145, n(С)=100. Обратимся к диаграмме (рис. 1).

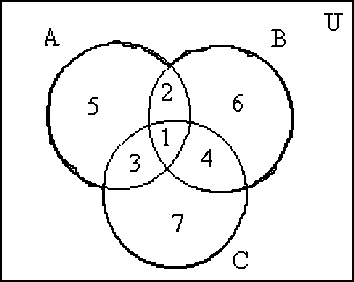
Рис. 1. Диаграмма Эйлера-Венна

М = 500

А – математика n(A) = 345

В – физика n(B) = 145

С – астрономия n(C) = 100

Пусть М = A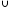В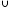С где А, В, С - пересекающиеся множества. Тогда разбиение множества М на классы можно представить в следующем виде:

M=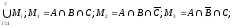

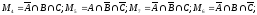
Множество студентов, посещающих 3 спецкурса:

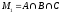= 10

Множество студентов, посещающих спецкурсы по математике и физике:

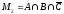= 30 - 10 = 20

Множество студентов, посещающих спецкурсы по математике и астрономии:

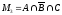= 25 – 10 = 15

Множество студентов, посещающих спецкурсы по физике и астрономии:

= 145 – 80 – 20 – 10 = 35

Множество студентов, посещающих только спецкурс по математике:

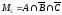= 345 – 10 – 20 – 15 = 300

Множество студентов, посещающих только спецкурс по физике:

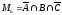= 80

Множество студентов, посещающих только спецкурс по астрономии:

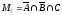= 100 -10 – 15 – 35 = 40

Множество студентов, посещающих 2 спецкурса:

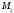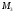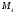+ + = 20 +15 +35 = 70

Ответ:

40 студентов посещают спец­курс только по астрономии. 70 студентов посещают два спецкурса.

2.1. Получить СДНФ, СКНФ, используя таблицу истинности. Построить ДНФ, КНФ, упростив выражение.

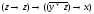
Построим таблицу истинности.

x	y	z					)
0	0	0	1	0	1	0	0
0	0	1	1	1	0	1	1
0	1	0	1	1	0	1	1
0	1	1	1	1	0	1	1
1	0	0	1	0	1	1	1
1	0	1	1	1	0	1	1
1	1	0	1	1	0	1	1
1	1	1	1	1	0	1	1

СДНФ =

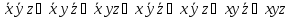
СКНФ =

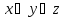
ДНФ =

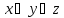
КНФ =

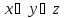
3.1. Упростить схему.

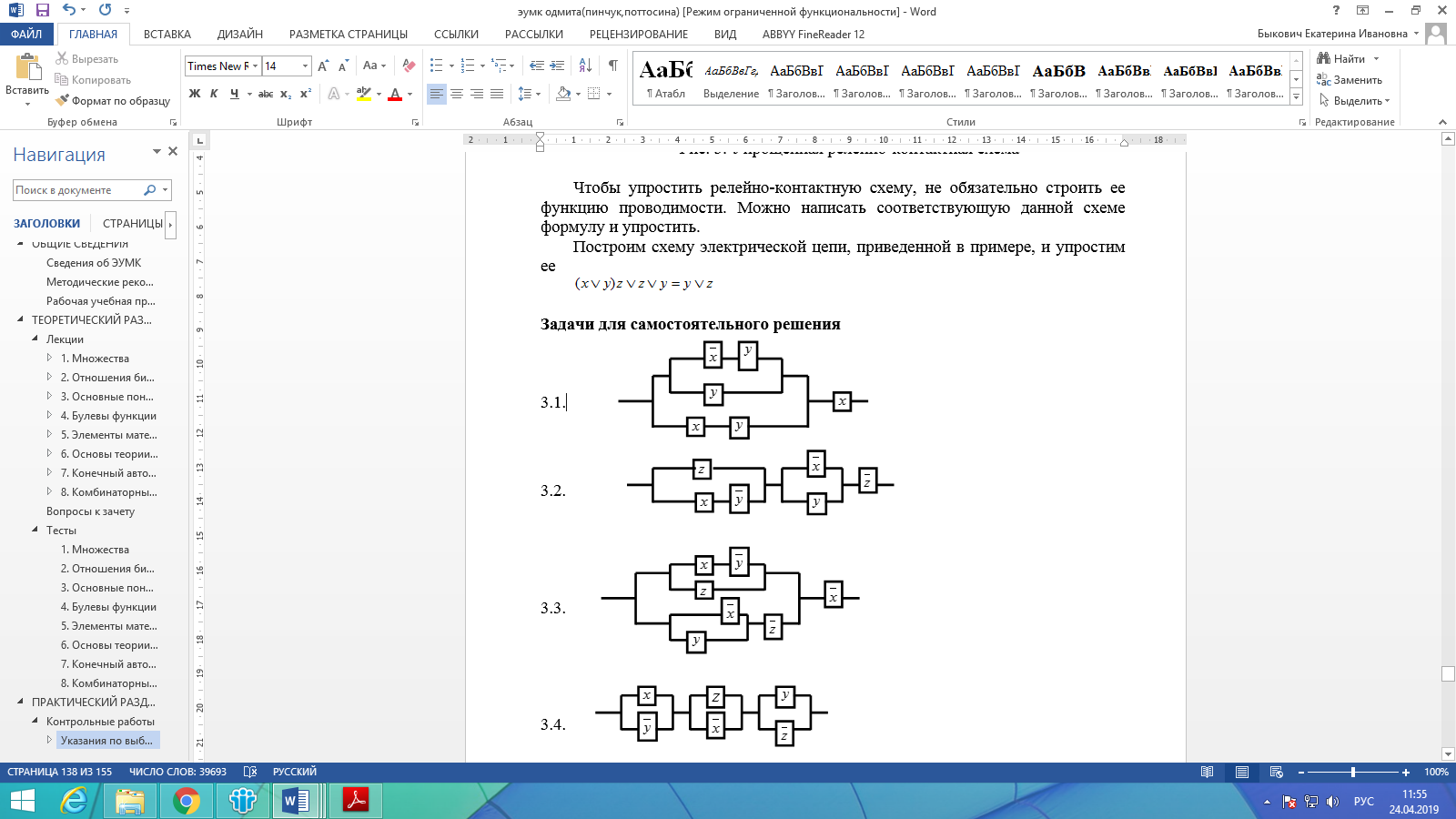
СДНФ=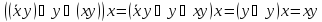

x	y				xy
0	0	1	0	0	0	0	0
0	1	1	1	1	0	1	0
1	0	0	0	0	0	0	0
1	1	0	0	1	1	1	1

4.1. Выяснить, каким из пяти замкнутых классов 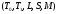принадлежит функция, заданная своим характеристическим множеством 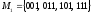. Построить полином Жегалкина.

Построим таблицу истинности для заданной функции.

x	y	z	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

Построим для функции f полином Жегалкина:

f=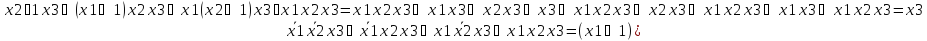

Определим принадлежность к классам :

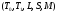Т₀: функция принадлежит классу Т₀, если на нулевом наборе она принимает значение 0. Соответственно, функция f принадлежит классу Т_0.

Т₁: функция принадлежит классу Т₁, если на единичном наборе она принимает значение 1. Соответственно, функция f принадлежит классу Т1_.

L: функция принадлежит классу L, если ее полином Жегалкина не содержит произведений. Полином Жегалкина функции = х3, полином не содержит произведений, поэтому функция f принадлежит классу L.

М: Функция принадлежит классу монотонных функция (М), если для любой пары наборов α и β таких, что α≤β, выполняется условие f(α)≤f(β). Функция f принадлежит классу М.

S:функция принадлежит классу самодвойственных функций S, если на противоположных наборах она принимает противоположные значения. Проверим: {0,0,0} и {1,1,1}: 0 и 1; {0,0,1} и {1,1,0}: 1 и 0; {0,1,0} и {1,0,1}: 0 и 1; {0,1,1} и {1,0,0}: 1 и 0. Таким образом функция f принадлежит классу S.
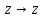
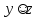
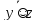
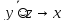
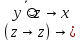