10. Классификация нагрузок

Нагрузки – внешние активные (заданные) силы.

По характеру действия нагрузки могут быть:

• Статические нагрузки почти не изменяются в тече­ние всего времени работы конструкции или меняются очень медленно (например, давление ферм на опо­ры).

• Динамические нагрузки(ударные) действуют непродолжительное время. Их воз­никновение связано в большинстве случаев с наличием значительных уско­рений и сил инерции.

По продолжительности действия принято различать:

• Примером постоянной нагрузки может слу­жить соб­ственный вес подшипника скольжения на кронштейн.

• Переменной нагрузке – многократно меняет величину. Действие такой нагрузки вызывает «усталость» металла

По способу приложения нагрузки бывают:

• Сосредоточенные нагрузки передают свое действие через очень малые площади. Примерами таких нагрузок могут служить давление колес железнодорожного вагона на рельсы, давление тележки тали на монорельс и т. д.

• Распределенные нагрузки действуют на сравнительно большой площади. Например, вес станка передается через станину на всю площадь соприкосновения с фундаментом. При решении задач статики для абсолютно твёрдого тела распределенную нагрузку можно заменить равнодействующей.

- равномерно-распределенная нагрузка : (q = const, q – интенсивность распр.нагрузки)

- неравномерно-распр-ная нагрузка: (q ≠ const)

11. Классификация элементов конструкций по их форме.

1)Брус (рисунок: а, б) – тело, у которого длина намного больше др. размеров тела. Брусья могут быть прямолинейными, криволинейными, постоянного и переменного сечения, плоскими и пространственными, иметь различные по форме сечения б).

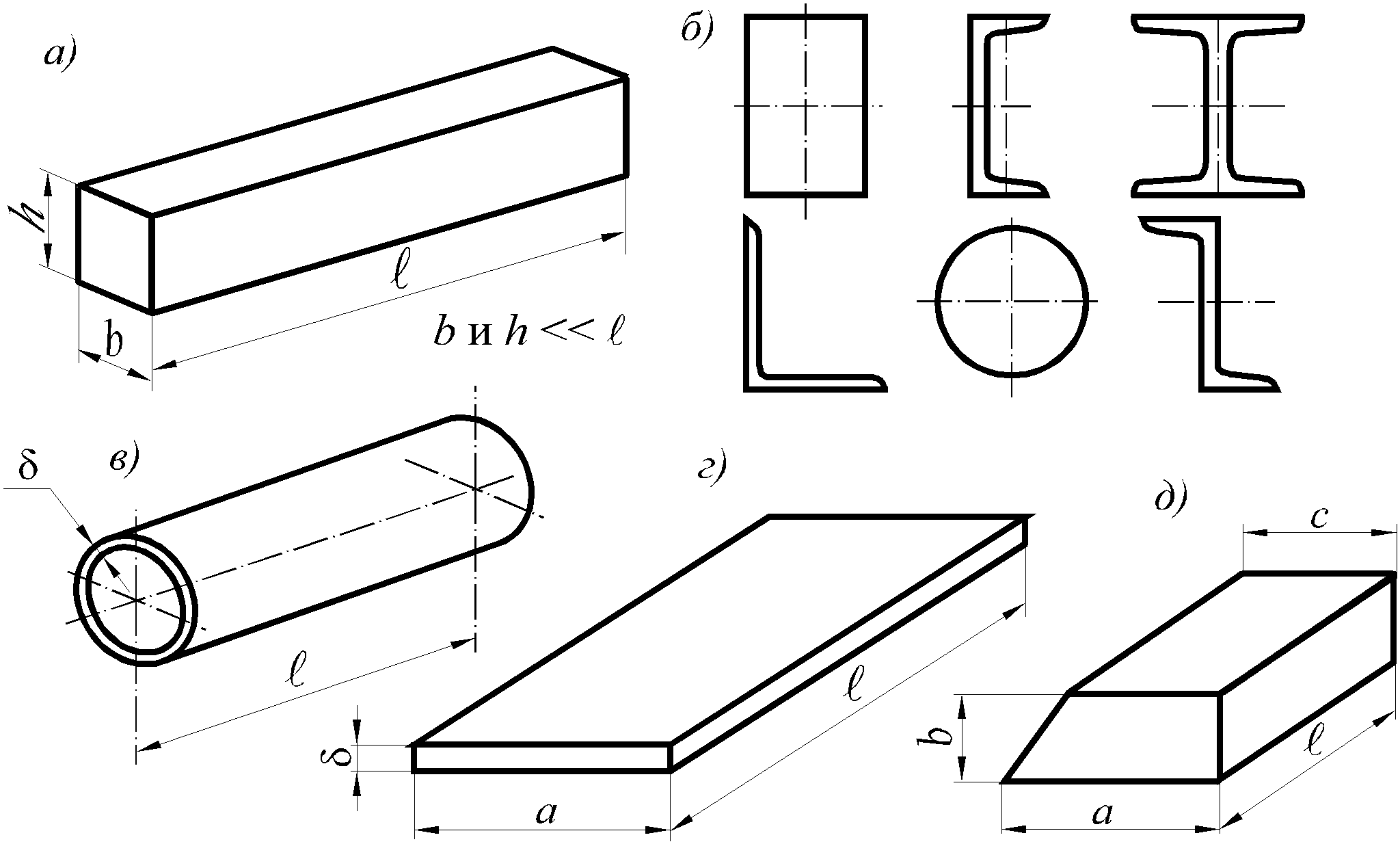
Осью бруса называется линия, соединяющая центры тяжести его поперечных сечений.

2) Брус с прямолинейной осью называется стержнем. , где L –длина, h – высота, d – толщина, L>>h>>d 3) Оболочка(рисунок в).  – тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с прочими размерами 4) Если поверхности оболочки плоские, то такой элемент называется пластиной (рисунок г). 5) Массив(рисунок д). – тело, у которого все три размера имеют один порядок

12. Метод сечений.

Под действием внешних сил в детали возникают внутренние силы упругости. Для определения внутренних усилий используется МЕТОД СЕЧЕНИЙ (РОЗУ).

РОЗУ заключается : в мысленном рассечении тела плоскостью и рассмотрение равновесия любой из рассеченных частей.

РОЗУ:

- разрезаем,

- отбрасываем (одну из отсеченных частей);

- заменяем (действие отброшенной части реакциями);

- уравновешиваем (оставшуюся часть).

Если тело находится в равновесии, то в равновесии находится любая из его частей. Внутр. Силы определяются из уравнений равновесия, составленных для рассматриваемой части тела.

13. Внутренние силовые факторы в поперечном сечении бруса.

Под влиянием внешей нагрузки реальные тела деформируются, в отличие от абсолютно твердого тела, изучаемого в курсе теоретической механики. При этом между рядом раположенными частицами тела воникают, по законам физики, внутренние силы. Если мысленно рассечь деформированный брус плоским перечным сечением на две части и привести внутренние силы, действующие со стороны одной части на другую - к центру тяжести (площади) поперечного сечения, получим ГЛАВНЫЙ ВЕКТОР R и ГЛАВНЫЙ МОМЕНТ M системы этих внутренних сил. Эти величины (R и M) имеют такой смысл:

Если мысленно заменить внутренние силы, действующие в сечении, силой R и моментом (парой сил) M (приложив их в центре тяжести поперечного сечения), то равновесие отсеченной части тела не нарушится. То есть R и M (совместно) являются статическим эквивалентом системы внутренних сил, действующих в сечении.

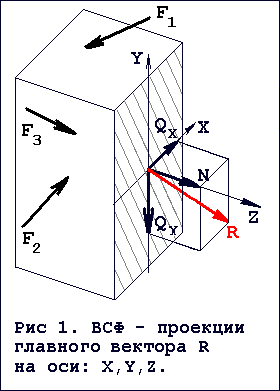
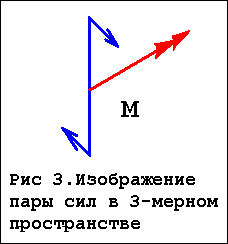
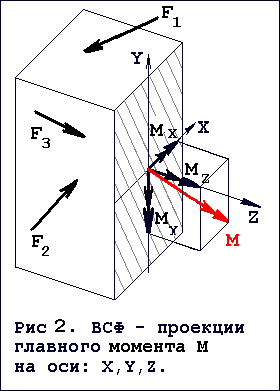
Рис. 1,2,3: Внутренние силовые факторы (ВСФ) в поперечном сечении бруса

Проекции главного вектора R и главного момента M на ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ поперечного сечения и ПРОДОЛЬНУЮ ось бруса называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ (ВСФ) в поперечном сечении. ВСФ (см рис 1) обозначаются:

Проекция R на ось Z т е N называется продольной силой.

Проекция R на ось Y т е QY называется поперечной силой.

Проекция R на ось X т е QX тоже называется поперечной силой.

Проекция M на ось Z т е MZ называется крутящим моментом.

Проекция M на ось Y т е MY называется изгибающим моментом (в горизонтальной плоскости XZ ).

Проекция M на ось X т е MX тоже называется изгибающим моментом (в вертикальной плоскости YZ ).

Примечание:

Существует два способа изображения пары сил:

1. В виде вектора - как показано на рис. 2

2. В виде пары сил.

Чтобы перейти от одного способа к другому применяется ПРАВИЛО БУРАВЧИКА (см рис 3)

 14.Напряжения в поперечном сечении бруса.

Продольная сила приложена в центре тяжести сечения. При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения.

• Напряжение – интенсивность распределения внутренних усилий по сечению.

Опыт показывает, что в сечениях, удаленных от зоны приложения внешней нагрузки справедлива гипотеза плоских сечений. Сечения плоские до деформации остаются плоскими и после деформации. Отсюда следует, что в этих сечениях нормальные напряжения распределены равномерно и определяются по формуле , Па, (1.1) где N- продольная сила [Н], А – площадь поперечного сечения [м²]. Нормальные напряжения  при сжатии определяются так же, как и при растяжении, но считаются отрицательными.  В тех случаях, когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно по­казывать закон их изменения по длине бруса в виде графи­ка - эпюры нормальных напряжений.

15. Гипотеза плоских сечений.

Изучая деформации при растяжении и сжатии обнаруживаем, что выполняются гипотезы плоских сечений и принцип смягчения граничных условий(принцип Сен-Венама) Гипотеза плоских сечений заключается: поперечное сечение бруса, плоское и перпендикулярное продольной оси после деформации остается плоским и перпендикулярным продольной оси.

Гипотеза плоских сечений была установлена Я. Бернулли в результате экспериментов: при растяжении стержня продольные и поперечные риски, нанесенные на его поверхности до деформации, остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния между ними (между поперечными рисками они увеличиваются, а между продольными – уменьшаются).

В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности.

Следовательно, сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений.