Статический момент площади сечения. Применение в расчетах.

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис.):

(3)

(4)

(5)

где yc – расстояние от центра тяжести всего плоского сечения до оси x; xc – расстояние от центра тяжести всего сечения до оси y.

Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

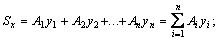
(6)

В формулах (6) введены обозначения: А1, А2, …, Аn – площади простых элементов, составляющих плоское сложное сечение; x1, y1, x2, y2, x3, y3, … , xn, yn – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.

1. Определение положения центра тяжести однородных плоских фигур.

Из выражений (4) можно определить координаты центра тяжести плоского сечения:

(7)

Для сложного поперечного сечения формулы (7) можно представить в следующем виде

(8)

Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х1, а также у и у1 имеют вид:

(9)

где параметры a, b показаны на следующем рисунке:

Указания:

1. Изменение положительного направления оси у вызывает изменение знака статического момента Sx. Аналогично, изменение положительного направления оси х вызывает изменение знака статического момента Sy.

2. Статический момент сечения равен нулю относительно любой оси, проходящей через центр тяжести этого сечения.

3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит через центр тяжести плоского сечения, а поэтому, согласно п.2, статический момент сечения относительно оси симметрии всегда равен нулю.

4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения лежит на пересечении этих осей симметрии.

3. Центробежный, полярный и осевые моменты инерции. Применение в расчетах.

Осевыми моментами инерции относительно осей x и y называют интегралы вида:

Полярным моментом инерции называется интеграл вида:

Если полюс совпадает с началом координатных осей, то выполняется условие

Осевые и полярные моменты инерции сечения всегда положительны.

Центробежным моментом инерции сечения называют интеграл вида

Центробежный момент инерции сечения может быть положительным, отрицательным и равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными. Если в симметричной фигуре хотя бы одна из осей координат совпадает с осью симметрии сечения, то центробежный момент инерции относительно такой пары осей равен нулю. Например, для сечения на рисунке имеем.

Рисунок - Симметричное сечение

Осевые, полярные и центробежные моменты инерции сечения имеют размерность – м⁴ (см⁴).

4 Моменты инерции простых сечений

Вычислим моменты инерции простейших фигур.

Прямоугольник

Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.

По определению  .

                      Рис. 4.8

Элемент площади равен   dA = bdy,

следовательно  .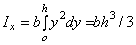

По формуле  , откуда, учитывая что   А = bh, y_c = 0,5h,   находим

.

Аналогично получим    и    .

Треугольник

Момент инерции относительно оси х, cовпадающей с основанием,

.

Но   dA = b(y)dy,   b(y) = (b/h)(h-y).

Cледовательно,

.

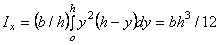Рис. 4.9

 

По формуле параллельного переноса  ,  откуда  .

Круг

Для  любых  центральных  осей   ,  поэтому   .

Как известно, полярный момент инерции круга равен  .

Рис. 4.10

 

Следовательно,  .

 

Кольцо  ( ).

Момент инерции относительно оси   (рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга:

.

Для тонкого кольца существует приближенная формула  , где   d_ср – средний диаметр, t - толщина кольца.