1.3.3. Основні теореми кодування

Загальні математичні принципи, викладені в Розділі 1.3.2, базуються на моделі системи передачі інформації, схема якої приведена на Рис. 1.7, і складається з джерела інформації, каналу та одержувача. У даному розділі в цю схему буде додана система зв'язку, і будуть розглянуті три основні теореми кодування, або подання, інформації. Як показано на Рис. 1.9, система зв'язку розміщена між джерелом і одержувачем, і складається з кодера і декодера, з'єднаних каналом зв'язку.

Терема кодування для каналу без шуму

Коли і інформаційний канал, і система зв'язку вільні від помилок, то основна роль останньої повинна зводитися до подання джерела в максимально компактній формі.

 

Рис. 1.9. Модель системи передачі інформації.

При цих умовах теорема кодування для каналу без шуму, також називають першою теорема Шеннона, визначає мінімально досяжну середню довжину кодового слова на символ джерела.

Джерело інформації з кінцевим ансамблем повідомлень (А,z) і статистично незалежними символами джерела, називається джерелом без пам'яті. Якщо виходом джерела є не один символ, а послідовність з n символів алфавіту, то можна вважати, що вихід джерела приймає одне з можливих значень, позначуваних з повного набору можливих послідовностей в n елементів: . Іншими словами, кожен блок , називається блоковою випадковою змінною, складається з n символів алфавіту A. (Позначення дозволяє відрізняти набір блоків від набору символів алфавіту A.) Імовірність окремого блоку , дорівнює і пов'язана з імовірностями окремих символів наступним співвідношенням:

де індекси використовуються для вказівки n символів алфавіту А, складових блок . Як і раніше, вектор (штрих означає, що використовується блокова випадкова змінна) позначає сукупне розподіл ймовірностей , і ентропія джерела дорівнює

Підставляючи (1.3-14) для і спрощуючи вираз, отримаємо:

Таким чином, ентропія блокового джерела інформації без пам`яті (який породжує блоки випадкових символів) у n разів більше, ніж ентропія відповідного джерела одиночних символів. Таке джерело називають n-кратним розширенням джерела одиночних символів (нерозширення джерела). Зауважимо, що одноразовим розширенням джерела є нерозширене джерело як таке.

Оскільки кількість інформації на виході джерела , є перші , розумним представляється кодування , за допомогою кодових слів довжини , де l-ціле число, таке що

Інтуїція підказує, що вихід джерела , повинен бути представлений кодовим словом, довжина якого є найближче ціле, превищує кількість інформації в . Множення (1.3-16) на і підсумовування по всіх , дає

або

де означає середню довжину кодового слова, яке відповідає n-кратному розширенню нерозширення джерела, тобто

Розділивши (1.3-17) на n, і враховуючи, що , отримаємо нерівність:

, (1.3-19)

яке перетворюється в граничному випадку в рівність:

(1.3-20)

Нерівність (1.3-19) встановлює першу теорему Шеннона для джерел без пам'яті, яка стверджує, що, кодуючи джерело безмежного розширення, можна досягти значення скільки завгодно близької до ентропії джерела . Незважаючи на те, що ми грунтувалися на припущенні про статистичну незалежність символів джерела, отриманий результат може бути легко розповсюджений на більш загальний випадок, коли поява символу джерела може залежати від кінцевого числа попередніх символів. Такі типи джерел (називаються марковськими джерелами) звичайно використовуються для моделювання міжелементних зв'язків на зображенні. Оскільки є точною нижньою гранню для вираження (цей вираз, згідно (1.3-20), прагне до при збільшенні ), то ефективність будь-якої стратегії кодування може бути виражена наступною формулою:

Приклад 1.7. Кодування з розширенням.

Джерело інформації без пам'яті з алфавітом має ймовірності символів і . Згідно (1.3-3), ентропія цього джерела дорівнює 0,918 біт/символ. Якщо символи і представлені однобітових кодовими словами 0 і 1, то біт/символ і результуюча ефективність кодування дорівнює , або 0,918.

У Таблиці 1.4 містяться і тільки що розглянутий код, і альтернативний спосіб кодування, заснований на двократному розширення джерела. У нижній частині таблиці наведені чотири блокових символу ( ), відповідних другому варіанту. Як випливає з (1.3-14), їх ймовірності рівні 4/9, 2/9, 2/9 і 1/9. Відповідно (1.3-18), середня довжина кодового слова при цьому буде дорівнює 17/9 = 1,89 біт/символ. Ентропія при двократному розширенні джерела дорівнює подвоєною ентропії нерозширення джерела, тобто 1,83 біт/символ, так що ефективність при другому варіанті кодування складе = 1,83 / 1,89 = 0,97.

Таблиця 1.4. Приклад кодування з розширенням.

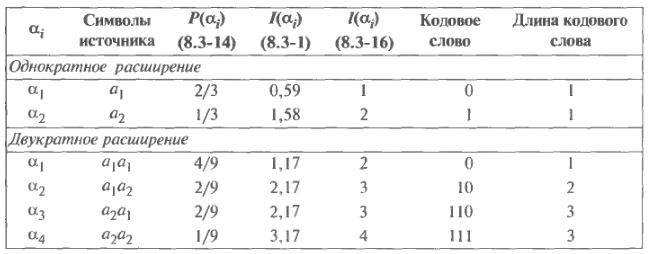
Це дещо краще, ніж ефективність нерозширення джерела, яка дорівнює 0,92. Як легко бачити, кодування дворазового розширення джерела скорочує середнє число бітів кодової послідовності на один символ джерела з 1 біт/символ до 1,89 / 2 = 0,94 біт/символ.

Теорема кодування для каналу з шумом

Якщо канал, зображений на Рис. 1.9 є каналом із шумом (тобто в ньому можливі помилки), то інтерес зміщується від завдання представлення інформації максимально компактним методом до задачі її кодування таким чином, щоб досягти максимально можливої надійності зв'язку. Питання, яке природно виникає, звучить наступним чином: наскільки можна зменшити помилки, утворені в каналі?

Приклад 1.8. Двійковий канал з шумом.

Припустимо, що ДСК має ймовірність помилки = 0,01 (тобто 99% всіх символів джерела передаються через канал правильно). Простий спосіб збільшення надійності зв'язку полягає в повторенні кожного повідомлення або кожного двійкового символу кілька разів. Наприклад, припустимо, що замість передачі одного символу 0 або 1, використовується кодове повідомлення 000 або 111. Імовірність того, що під час передачі трьохсимвольного повідомлення не виникне помилки, дорівнює , або Імовірність однієї помилки буде , двох , а ймовірність трьох помилок складе . Оскільки імовірність помилки при передачі одного символу становить менше 50%, то одержуване повідомлення може бути декодовано методом голосування трьох отриманих символів. Вірогідність невірного декодування трьохсимвольного кодового слова дорівнює сумі імовірностей помилок в двох символах і в трьох символах, тобто . Якщо ж у слові немає помилок, або всього одна помилка, то воно буде декодовано вірно. Таким чином, для = 0,01 ймовірність помилки при передачі зменшилася до значення 0,0003.

Розширюючи тільки що описану схему повторення, можна досягти як завгодно малої результуючої помилки передачі. У загальному випадку, це здійснюється кодуванням n-кратного розширення джерела при використанні K-символьної кодової послідовності довжини r, де . Ключовим питанням при такому підході є вибір в якості допустимих кодових слів тільки деякого числа з можливих кодових послідовностей, а також формулювання вирішального правила, оптимізуючого ймовірність правильного декодування. У попередньому прикладі, повторення кожного символу джерела три рази еквівалентно кодуванню нерозширення двійкового джерела, використовуючого лише два з = 8 можливих кодових слів. Два допустимих коду - це 000 і 111. Якщо на декодер надходить якийсь інший (недопустимий) код, то вихід визначається голосуванням по більшості з трьох кодових бітів.

Джерело інформації без пам'яті породжує інформацію зі швидкістю (в одиницях інформації на символ), рівної ентропії джерела . У разі n-кратного розширення, джерело створює інформацію зі швидкістю одиниць інформації на символ. Якщо інформація кодується так, як у попередньому прикладі, то максимальна швидкість кодованої інформації дорівнює , і вона досягається у випадку, коли всі допустимі кодові слова рівноймовірні. У такому випадку говорять, що код розміру і довжиною блоку має швидкість коду одиниць інформації на символ.

Друга теорема Шеннона [Shаппоп, 1948], також називається теоремою кодування для каналу з шумом, підтверджує наступне. Для будь-якого , де C є пропускна здатність каналу без пам'яті, існує код довжини r, де r-ціле, має швидкість R, таку, що ймовірність помилки блокового декодування не перевищує будь-якого наперед заданого з інтервалом . Таким чином, імовірність помилки можна зробити як завгодно малою, за умови, що швидкість кодових повідомлень менше або дорівнює пропускної здатності каналу.

Теорема кодування джерела (про взаємозв'язок швидкості і спотворення)

Теореми, розглянуті до справжнього моменту, встановлюють фундаментальні межі безпомилкової зв'язку як по надійним, так і по ненадійним каналам. У даному розділі ми повернемося до випадку каналу без помилок, але в цілому процес передачі інформації може бути не точним. Головним завданням системи зв'язку в такий послідовності є «стиснення інформації», можливо, за рахунок деякого її спотворення. У більшості випадків середня помилка, яку вносить стисненням, обмежується деякими максимально допустимим рівнем D. Ми хочемо знайти найменшу допустиму швидкість як функцію заданого критерію точності, при якій інформація може бути передана від джерела до одержувача. Вирішенням цієї конкретної проблеми займається розділ теорії інформації, називається теорія взаємозв'язку швидкості та спотворення.

Нехай джерело інформації і вихід декодера на Рис. 1.9 визначені кінцевими ансамблями (А, z) і (В, z) відповідно. Припускається, що канал на Рис. 1.9 є каналом без помилок, так що матриця каналу Q, Яка пов'язує z з v згідно (1.3-6), може розглядатися як визначальна тільки сам процес кодування-декодування. Оскільки процес кодування-декодування є детермінованим, описує деякий ідеальний канал без пам'яті, що імітує ефект стиснення і відновлення інформації. Всякий раз, коли джерело породжує вихідний символ , останній представляється деяким кодовою символом, який в результаті декодується у вихідний символ з імовірністю (див. Розділ 1.3.2).

Постановка задачі кодування джерела, при якій середня величина спотворення не повинна перевищувати рівня D вимагає методу кількісної оцінки величини спотворення для будь-якого виходу джерела. Для простого випадку нерозширення джерела може бути використана ненегативна функція вартості , називається мірою спотворення, визначальна величину «штрафу», виникає у випадку, коли вихід джерела відтворюється на виході декодера . Вихід джерела є випадковою величиною, тому спотворення також є випадковою величиною, середнє значення якої дорівнює

Запис підкреслює, що середнє спотворення є функція процедури кодування-декодування, яка (як уже зазначалося раніше) моделюється матрицею каналу . Конкретна процедура кодування-декодування називається D-точною тоді і тільки тоді , коли середнє спотворення менше або дорівнює D. Таким чином, набір D-точних процедур кодування-декодування може бути записаний у вигляді:

Оскільки кожна процедура кодування-декодування визначається матрицею каналу Q, то середня інформація, що отримується при спостереженні одиничного виходу декодера, може бути порахована відповідно (1.3-12). Отже, ми можемо визначити найменшу допустиму швидкість як функцію спотворення виразом

тобто як мінімальне значення (1.3-12) на множині всіх D-точних кодів. Зауважимо, що залежить від значень ймовірностей в векторі z і елементів матриці Q, а мінімум в правій частині (1.3-25) береться по Q. Якщо D = 0, то менше або дорівнює ентропії джерела, тобто .

Рівняння (1.3-25) визначає мінімально можливу швидкість як функцію спотворення, при якій інформація від джерела може бути доставлена ​​одержувачу за умови, що середнє спотворення менше або дорівнює D. Щоб обчислити цю швидкість, тобто , ротрібно мінімізувати значення , що задається (1.3-12), шляхом вибору підходящої матриці Q (або ) за умови виконання наступних обмежень:

,

і

Формули (1.3-26) і (1.3-27) виражають основні властивості матриці каналу : її елементи повинні бути невід'ємними і, оскільки будь-якому вхідному символу повинен відповідати якийсь вихід, сума елементів по будь-якому стовпцю матриці повинна бути рівна 1. Рівняння (1.3-28) показує, що мінімальна швидкість досягається при максимально допустимому спотворенні.

Приклад 1.9. Обчислення швидкості як функції спотворення для двійкового джерела без пам'яті.

Розглянемо двійковий джерело без пам'яті з рівноімовірними символами джерела {0, 1} і простою мірою спотворення

де - одинична дельта-функція. Оскільки якщо і 0 в інших випадках, то кожна помилка кодування-декодування вважається за одну одиницю спотворення. Для знаходження може бути використано варіаційне числення, а саме метод Лагранжа знаходження умовного екстремуму. Розглянемо функцію Лагранжа

яка додатково залежить від множників Лагранжа , , ..., . Прирівняємо її похідні по змінним до нуля (тобто = 0), і вирішимо систему, що складається з отриманих рівнянь разом з рівняннями зв'язків (1.3-27) і (1.3-28), для невідомих і , , ..., . Якщо отримані значення не негативні, тобто задовольняють (1.3-26), це означає, що знайдено вірне рішення. Для певної вище пари джерела і спотворення, отримаємо наступні 7 рівнянь (з 7-ма невідомими):

Послідовність алгебраїчних перетворень приводить до наступних результатів:

так що

Оскільки було задано, що символи джерела рівноймовірно, то максимальне можливе спотворення дорівнює 1/2. Таким чином і елементи матриці Q відповідають (1.3-12) для всіх D.

 Взаємна інформація, пов'язана з Q і раніше визначеним двійковим джерелом, обчислюється з використанням (1.3-12). Відповідно помітив схожість матриці Q і матриці двійкового симетричного каналу, можна відразу написати:

.

Це випливає з результату Прикладу 1.6 при підстановці = 1/2 і в вираз . Швидкість як функція спотворення може бути отримана прямо з (1.3-25):

.

Останнє спрощення засноване на тому обставину, що для заданного D різницю приймає єдине значення, за замовчуванням є мінімумом. Результуюча функція показана графічно на Рис. 1.10; ця форма типова для більшості графіків швидкості як функції спотворення. Відзначимо точку максимуму D, позначену , таку, що для всіх . Крім того, завжди позитивна, монотонно убиває, і опукла вниз на відрізку (0, ).

Для простих джерел і заходів спотворення, швидкість як функція спотворення може бути обчислена аналітично, як і в попередньому прикладі. Більше того, коли аналітичні методи не працюють, то можуть використовуватися сходяться ітеративні алгоритми, зручні для чисельної реалізації на комп'ютерах.

Рис. 1.10. Швидкість як функція спотворення для двійкового симетричного джерела.

Після того, як обчислили на , теорема кодування джерела стверджує, що для будь-якого існує такий код довжини r і швидкості , що середнє спотворення на символ задовольняє умові . Важливий практичний наслідок даної теореми і теореми кодування для каналу з шумом полягає в тому, що вихід джерела може бути відновлений декодером з довільно малою ймовірністю помилки , за умови, що канал має пропускну спроможність . Цей останній результат відомий як теорема про передачу інформації.