1.5. Стиснення з втратами

На відміну від викладеного в попередньому розділі підходу до кодування без втрат, кодування з втратами засноване на виборі балансу між точністю відновлення зображення і ступенем його стиснення. Якщо допустити появу спотворень в кінцевому результаті кодування (які можуть бути, а можуть і не бути помітними), то можливо значне збільшення коефіцієнта стиснення. Фактино, багато методи стиснення з втратами можуть цілком пізнавано відновлювати одноколірні зображення виданих, стислих з кофіцієнтами більш ніж 100:1, а також відтворювати фактично відрізнити від оригіналу зображення при коефіцієнтах стиснення від 10:1 до 50:1. У той же час методи стиснення без втрат рідко добиваються коефіцієнтів кращих, ніж 3:1. Як показано в Розділі 1.2, принципова різниця між структурними схемами цих двох підходів полягає в наявності або відсутності блоку квантування на Рис. 1.6.

1.5.1. Кодовання з передбаченням

У цьому розділі в модель кодування, введену в Розділі 1.4.4, буде доданий квантувач і проведений пошук компромісу між точністю відновлення і ступенем стиснення. Як видно з Рис. 1.21, між кодером символів і точкою, в якій формуєся помилка передбачення, поміщається квантователь, який бере на себе функцію визначення найближчого цілого від величини, отримаї на виході кодера без помилок. Він відображає помилку передбачення в обмежений набір (квантованих) значень сигналу на виході , величина різниці між якими (тобто точність квантування) визначає ступінь стиснення і величину спотворення, виниклого в результаті такого кодування.

Для адаптації моделі до введення блоку квантувача, безпомилковий кодер на Рис. 1.19 (а) повинен бути змінений так, щоб передбачення, що генеруються кодером і декодером, були ідентичними.

а)

б)

Рис. 1.21. Модель кодування з втратами з передбаченням: (а) кодер, (б) декодер.

Як видно на Рис. 1.21 (а), це досягається приміщенням кодера з втратами в ланцюг зворотного зв'язку провісника, де його вхід, позначений , формується як функція від попереднього передбачення і помилки квантування. Таким чином,

де. та ж, що була визначена в формулі (1.4-7) в Розділі 1.4.4. Схема зі зворотним зв'язком запобігає накопиченню помилки на виході кодера. Як видно з Рис. 1.21 (б), вихід декодера також задається формулою (1.5-1).

Приклад 1.16. Дельта-модуляція.

Дельта-модуляція (ДМ) є простим, але добре відомим способом кодування з втратами, в якому провісник і квантувач визначаються таким чином:

і

де - коефіцієнт передбачення (зазвичай менше 1), а - позитивна константа. Вихід квантувача , може бути представлений єдиним бітом (див. Рис. 1.22 (а)), так що кодер символів на Рис. 1.21 (а) може використовувати 1-бітовий рівномірний код. Результуюча швидкість ДМ-коду складе 1 біт/піксель.

На Рис. 1.22 (в) ілюструється механізм дельта-модуляції; в таблиці наведені значення сигналів при стисненні і відновленні наступної вхідної послідовності: {14, 15, 14, 15, 13, 15, 15, 14, 20, 26, 27, 28, 27, 27, 29, 37, 47, 62, 75, 77, 78, 79, 80, 81, 81, 82, 82} при = 1 = 6,5. Процес починається з передачі неспотвореного значення першого елемента декодеру. При початкових умовах встановлених як на стороні кодера, так і на стороні декодера, решту значення на виході можуть бути визначені повторними обчисленнями за формулами (1.5-2), (1.4-5) , (1.5-3) та (1.5-1). Так, при n = 1 отримаємо : (тому, що > 0), , і результуюча помилка відновлення складає (15 - 20,5), або -5,5 рівнів яскравості.

а) б)

в)

Рис. 1.22. Приклад дельта-модуляції.

На Рис. 1.22 (6) графічно показані дані, представлені в таблиці на Рис. 1.22 (в). Тут показаний вхідний сигнал ( ) і вихід декодера ( ). Зауважимо, що на ділянці швидкого зміни вхідного сигналу від n = 14 до 19, де виявляється занадто малим для відстеження великих змін на вході, виникає спотворення, що називається перевантаження по крутизні. Крім того, на ділянці від n = 0 до 7, де виявляється занадто велике для відображення малих змін на вході або щодо плавних ділянок, виникає шум гранулярності. На більшості зображень ці два явища призводять до розмивання контурів і появи областей з високою зернистістю або шумом (тобто до спотворення гладких об'єктів).

Спотворення, зазначені в попередньому прикладі, є загальними для всіх видів кодування з втратами з прогнозом. Наскільки великі ці спотворення, залежить від обраних методів квантування та передбачення в цілому. Незважаючи на взаємозв'язки між ними, зазвичай провісник розраховується в припущення відсутності помилок квантування, а квантователь - виходячи з умов мінімізації своїх власних помилок. Таким чином, і провісник і квантователь розраховуються незалежно один від одного.

Оптимальні провісники

Оптимальні провісники, що використовуються в більшості використовуємих кодерів з пророкуванням, мінімізують середній квадрат помилки передбачення кодера:

де Е { } - математичне сподівання, за умови, що

і

Таким чином, критерій оптимізації вибирається так, щоб мінімізувати середній квадрат помилки пророкування, помилка квантвання вважається малою ( ), а пророкування представляє собою лінійну комбінацію значень m попередніх елементів. Ці обмеження не є строго необхідними, але вони значно спрощують аналіз, і, в той же час, дозволяють зменшити обчислювальну складність провісника. Отримується в результаті підхід до кодування з пророкуванням відомий як диференціальна імпульсно-кодова модуляція (ДІКМ).

За таких умов проблема побудови оптимального провісника зводиться до відносно простої задачі вибору m коефіцієнтів провісника, які будуть мінімізувати наступний вираз:

Диференціюючи рівняння (1.5-7) по кожному з коефіцієнтів, прирівнюючи значення похідних до нуля, і вирішуючи отримуємо систему рівнянь за умови, що має нульове середнє і дисперсію , отримаємо

де є зворотною матрицею наступної матриці автокорреляції розмірами :

а і є -елементними векторами:

Таким чином, для будь-якого вхідного зображення, коефіцієнти, які мінімізують (1.5-7), можуть бути визначені за допомогою послідовності елементарних матричних операцій. Більш того, коефіцієнти залежать лише від значень автокореляцій пікселів на початковому зображенні. Дисперсія помилки пророкування, що виникає при використанні цих оптимальних коефіцієнтів, буде рівна

Хоча заснований на рівнянні (1.5-8) спосіб обчислень достатньо простий, практичне обчислення значень автокореляцій, необхідних для формування і настільки важко, що особисті передбачення (ті, в яких коефіцієнти передбачення обчислюються для зображення індивідуально) майже ніколи не застосовуються. У більшості випадків вибирається набір загальних кокоефіцієнтів, який вираховується шляхом оцінювання деякої простої моделі зображення та підстановки відповідних значень автокореляції в (1.5-9) та (1.5-10). Так, у випадку, якщо передбачається двовимірним Марковським джерелом (див. Розділ 1.3.3) з роз’єднаною автокореляційною функцією

і узагальненим лінійним провісником четвертого порядку

то результуючі оптимальні коефіцієнти будуть рівні

де - горизонтальний, а - вертикальний коефіцієнти корреляції розглянутого зображення.

Нарешті, звичайно потрібно, щоб сума коефіцієнтів передбачения в (1.5-6) ​​була менше або дорівнює одиниці, тобто

Це обмеження накладається для того, щоб гарантувати, що значення на виході провісника буде залишатися всередині допустимого діапазону рівнів яскравостей, а також, щоб зменшити вплив шумів передачі, вплив яких зазвичай проявляється на відновленому зображенні у вигляді горизонтальних смуг. Важливо також зменшити чутливість ДІКМ декодера по відношенню до вхідного шуму, тому що єдина перешкода (при визначених умовах) може розповсюджуватися на весь подальший вихід. Це означає, що вихід декодера може виявитися нестійким. Запровадження додаткового обмеження в (1.5-15) - що сума повинна бути строго менше одиниці - дозволяє зменшити протяжність впливу шуму на вході декодера до декількох вихідних значень.

Приклад 1.17. Порівняння методів передбачення.

Розглянемо помилки пророкування, що виникають при ДІКМ кодуванні напівтонового зображення на Рис. 1.23, в припущенні нульовою помилки квантування і при використанні кожного з наступних чотирьох провісників:

Рис. 1.23. Напівтонове монохромне зображення розмірами 512x512 пікселів

де і означають вертикальний і горизонтальний градієнти в точці (х, у). У формулах (1.5-16) - (1.5-18) заданий досить стійкий набір кокоефіцієнтів , що забезпечує задовільні характеристики в широкому діапазоні зображень. Адаптивний передбачувач в (1.5-19) призначений для поліпшення передачі контурів. Він вимірює локальні характеристики зображення по напрямкам ( і ) і вибирає провісник, відповідний виміряної оцінці.

а) б)

в) г)

Рис. 1.24. Порівняння чотирьох методів лінійного передбачення

На Рис. 1.24 (а) - (г) у вигляді зображень показані помилки передбачень, що виникають при використанні формул (1.5-16) - (1.5-19). Як видно, помітність помилки зменшується зі збільшенням порядку передбачення. Стандартні відхилення помилок передбачення дають близькі результати: вони рівні, відповідно, 4,9, 3,7, 3,3 і 4,1 рівня яскравості.

Оптимальне квантування

Східчаста функція квантування , показана на Рис. 1.25, є непарною функцією , тобто ; таким чином, вона повністю задається набором з пар значень і для першого квадранта на графіку. Ці точки розривів задають скачки функції і називаються пороговими рівнями ( ) і рівнями квантування ( ) квантувача. Зазвичай вважають, що вхідне значення відображається в рівень квантування , якщо знаходиться в напівінтервалі при , і, відповідно, при .

Проблема побудови квантователя полягає у виборі найкращих значень і для конкретного критерію оптимізації та щільності розподілу ймовірностей . Якщо критерієм оптимізації,

Рис. 1.25. Типова функція квантування.

який може бути як статистичної, так і візуальною мірою, є мінімізація середнього квадрата помилки квантування (тобто ), а також, якщо є парною функцією, умовами мінімальної помилки [Мах, 1960] є:

і

Рівняння (1.5-20) показує, що оптимальні рівні квантування є точками центрів тягарів областей під по кожному з інтервалів квантування, розділених пороговими рівнями, а рівняння (1.5-21) - що порогові рівні повинні розташовуватися посередині між рівнями квантування. Умови (1.5-22) є наслідком того, що q- непарна функція. Таким чином, для будь-якого L і , такі пари і для яких виконуються рівняння (1.5-20) - (1.5-22), є оптимальними в сенсі среднеквадрі-тичної помилки. Відповідний квантователь називається L-рівневим квантувачем Ллойда-Макса.

Таблиця 1.10. Квантователь Ллойда-Макса для щільності розподілу ймовірностей Лапласа з одиничною дисперсією.

У таблиці 1.10 наведені порогові рівні і рівні квантування 2-, 4-, і 8-рівневого квантувача Ллойда-Макса для функції щільності розподілу ймовірностей Лапласа з одиничною дисперсією (1.4.10). Ці значення були отримані чисельним методом [Paez, Glisson, 1972], оскільки отримання точного, або явного, рішення рівнянь (1.5-20) - (1.5-22) для більшості нетривіальних досить важко. Три представлених квантувача забезпечують фіксовані швидкості коду, рівні, відповідно, 1, 2 і 3 бітам/піксель. Оскільки Таблиця 1.10 була побудована для розподілення з одиничною дисперсією, то значення порогових рівнів і рівнів квантування для випадків виходять простим множенням табульованих значень на величину стандартного відхилення наявного розподілу щільності ймовірностей. В останньому ряду таблиці наведені розміри кроку оптимального рівномірного квантувача, який одночасно задовільняє рівняння (1.5-20) - (1.5-22), а також додатковим обмеженням.

Якщо в кодере з втратами з пророкуванням (Рис. 1.21 (а)) використовується кодер символів, що породжує нерівномірний код, то при одній і тій же вихідній точності оптимальний рівномірний квантувач з кроком розміру в забезпечить більш низьку швидкість коду (для щільность розподілу ймовірностей Лапласа), ніж рівномірно кодований вихід квантувача Ллойда-Макса.

Як квантователь Ллойда-Макса, так і оптимальний рівномірний квантувач не є адаптивними, і набагато кращий результат можна отримати, адаптуючи рівні квантування відповідно до змін локальних характеристик зображення. Теоретично, області з плавними змінами яскравості можуть квантуватись на більш дрібні рівні, тоді як області швидких змін - на більш грубі. Такий підхід одночасно скорочує як шум гранулярності, так і перевантаження по крутизні, вимагаючи при цьому мінімальне збільшення кодової швидкості. Однак такий компроміс значно збільшує складність квантувача.

Приклад 1.18. Ілюстрація процесів квантування і відновлення.

На Рис. 1.26 (а), (в) і (д) представлені відновлені зображення, отримані комбінацією 2-, 4-, або 8-рівневого квантувача Ллойда-Макса та двовимірного провісника (1.5-18). Параметри квантователя визначалися шляхом множення табличних значень порогових рівнів та рівнів квантування для квантователя Ллойда-Макса (див. Таблицю 1.10) на

а) б)

в) г)

д) е)

  Рис. 1.26. Результати ДІКМ кодування з втратами зображення на Рис. 1.23: (а) 1,0; (б) 1,125; (в) 2,0; (г) 2,125; (д) 3,0; (е) 3,125 біта/піксель.

на стандартне відхилення неквантованої помилки двовимірного передбачення, наведене в попередньому прикладі (тобто 3,3 рівня яскравості). Зверніть увагу, що контури на декодованих зображеннях розмиті через перевантаження по крутизні. Цей ефект сильно помітний на Рис. 1.26 (а), де використувався дворівневий квантувач, але вже проявляється менше на Рис. 1.26 (в) і (д), які отримані за допомогою 4- і 8-рівневий квантувач. На Рис. 1.27 (а), (в) і (д) показані посилені різниці між вихідним (на Рис. 1.23) і отриманими декодованими зображеннями.

Для отримання декодованого зображення на Рис. 1.26 (6), (г) і (е), помилки яких показані на Рис. 1.27 (6), (г) і (е), викоритовувався метод адаптивного квантування, в якому для кожного блоку з 16 елементів вибирався найкращий (в сенсі середнього квадрата помилки) з чотирьох можливих квантувачів. Ці чотири квантувача є варіантами масштабування раніше описаного оптимального квантувача Ллойда-Макса. Масштабні коефіцієнти були 0,5, 1,0, 1,75. і 2,5. Оскільки для зазначення номера вибраного квантувача до кожного блоку додавався 2-бітовий додатковий код, то накладні витрати склали 0,125 біта/піксель. Зверніть увагу на значне зменшення видимих ​​помилок, досягнуте завдяки незначному збільшенню швидкості коду.

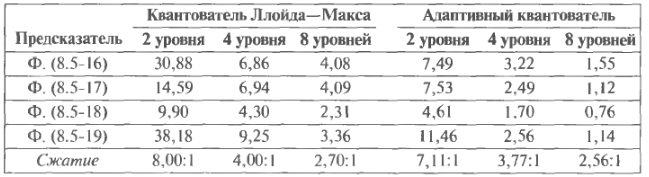
У Таблиці 1.11 наведені значення стандартних відхилень помилок (1.1-8) різницевих зображень на Рис. 1.27 (а) - (е) ​​усіх чотирьох варіантів вищенаведених провісників (1.5-16) - (1.5-19) при різних комбінаціях провісника і квантувача. Зауважимо, що з точки зору середнього квадрата помилки, дворівневий адаптивний квантувач дає настільки ж добрі результати, що і чотирьохрівневий неадаптівний. Більш того, чотирьохрівневий адаптивний квантувач дає кращі результати, ніж восьмирівневий неадаптівний. Взагалі, чисельні результати показують, що тенденції зміни величини помилки для провісників (1.5-16), (1.5-17) і (1.5-19) збігаються з аналогічними характеристиками провісника (1.5-18). У нижньому рядку таблиці наведена величина стиснення, що досягається кожним з розглянутих методів. Зауважимо, що значні зменшення стандартного відхилення помилки, що досягається адаптивним квантувачем, не приводить до істотного поліпшення характеристик стиснення.

Таблиця 8.11. Значення стандартних відхилень помилок при ДІКМ коди ¬ рованії з втратами.

а) б)

в) г)

д) е)

Рис. 1.27. Зображення підсилених в 8 разів помилок ДІКМ кодування на Рис. 1.26.