1.4.3. Кодування бітових площин

Іншим ефективним підходом до скорочення міжелементної надлишковості є обробка бітових площин зображення окремо. Метод, названий кодування бітових площин, заснований на концепції попереднього розкладання багатоградаціного зображення (чорно-білого або кольорового) на серію двійкових зображень, і подальшого кодування кожного з них за допомогою одного або декількох добре відомих алгоритмів стиснення двійкових зображень. Нижче розглядаються найбільш відомі підходи до розкладання і аналізуються деякі з широко використовуємих методів стиснення.

Розкладання на бітові площини

Рівні яскравості m-бітового чорно-білого зображення можуть бути представлені у формі полінома з основою 2:

Заснований на цій властивості простий метод розкладання багатоградаційного зображення на безліч двійкових зображень полягає у поділі m коефіцієнтів полінома на m однобітових бітових площин. Площина нульового порядку утворюється виділенням бітів (або коефіцієнтів) кожного елемента, а бітова площину порядку ( ) - виділенням бітів . Взагалі, кожна бітова площина нумерується від 0 до і формується установкою значень її елементів рівним значенням відповідних бітів або поліноміальних коефіцієнтів елементів вихідного зображення. Недолік, властивий даному підходу, полягає в тому, що малі зміни яркостей можуть істотно впливати на складність бітових площин. Так, якщо піксель зі значенням 127 (01111111) змінить значення на 128 (10000000), то у всіх бітових площинах відбудеться перехід з 1 на 0 (або з 0 на 1). Наприклад, оскільки старші біти двох двійкових кодів для 127 і 128 розрізняються, то піксель сьомий бітової площині, що мав первинне значення 0, змінить значення на 1.

Альтернативним підходом до розкладання, який зменшує ефект перенесення бітів при малих змінах яркостей, є представлення зображення у вигляді m-бітового коду Грея. Відповідний код Грея, записується у вигляді , може бути визначений за коефіцієнтами полінома (1.4-2) наступним чином:

Тут знак означає операцію виключного АБО. Цей код має ту унікальну властивість, що йдуть один за одним кодові слова розрізняються тільки в одній бітової позиції. Таким чином, малі зміни яскравості з меншою ймовірністю будуть впливати на всі m-бітових площин. Наприклад, якщо відбувається перехід з рівня 127 на рівень 128, то перехід з 0 на 1 виникне тільки в 7-й бітової площині, оскільки коди Грея для 127 і 128 дорівнюють 11000000 і 01000000 відповідно.

Приклад 1.13. Кодування бітових площин.

На Рис. 1.14 (а) і (б) представлені зображення розмірами 1024 1024, використовувані для ілюстрації методів стиснення, описується в частині, що залишилася в даному розділі. Напівтонове зображення дитини було отримано ПЗС камерою високого розширення.

а) б)

 Рис. 1.14. Зображення розмірами 1024x1024 елемента: (а) напівтонове 8-бітове зображення, (б) двійкове зображення.

7 біт

6 біт

5 біт

4 біт

3 біт

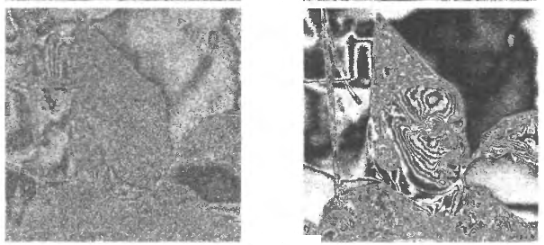
2 біт

1 біт

0 біт

Рис. 1.15. Чотири старших бітових площині зображені на Рис. 1.14 (а): лівий стовбець - двійковий код, правий стовбець - код Грея.

Двійкове (двохградаційне) зображення тексту документа на право володіння, підготовленого президентом США Ендрю Джексоном в 1796 р., було оцифровано на планшетному сканері. На Рис. 1.15 і 1.16 зображення дитини представлено у вигляді восьми двійкових бітових площин, а також у вигляді восьми бітових площин коду Грея. Зауважимо, що бітові площини високих порядків є значно менш складними, ніж їх доповнення низьких порядків; тобто вони містять протяжні області з меншим кіль ¬ кість деталей або випадкових змін. Крім того, бітові площини коду Грея, є менш складними, ніж відповідні двійкові бітові площини.

Кодування областей сталості

Простим, але ефективним методом стиснення двійкових зображень чи бітових площин, є використання спеціальних кодових слів для ідентифікації великих областей, що складаються з сусідніх одиниць або нулів. Відповідно до одного з таких підходів, що називається кодування областей сталості (КОС), зображення розбивається на блоки розмірами пікселів, які класифікуються як цілком білі, цілком чорні, або змішаної яскравості. Потім найбільш імовірною або часто зустрічається категорії присвоюється 1-бітове кодове слово 0, а інші дві категорії отримують 2-бітові коди 10 і 11. Стиснення досягається за рахунок того, що бітів, які в звичайному випадку необхідні для подання області довільних значень, замінюються 1 - або 2-бітовим кодовим словом, що вказує на область сталості. Звичайно ж, код, що привласнюється категорії областей змішаної яскравості, використовується в якості префікса, за яким йде набір з бітів, що містяться в блоці.

При стисненні текстових документів, які переважно є білими, може використовуватися кілька більш простий підхід, який полягає в тому, що білі блоки кодуються кодом 0, а всі інші (включаючи цілком чорні) блоки - кодом 1, за яким слідує набір бітів в блоці. Перевага такого підходу, що називається пропуском білих блоків (ПББ), виникає за рахунок запропонованих структурних властивостей стисненого зображення. Якщо ж і зустрічаються невелика кількість цілком чорних блоків, то вони будуть віднесені до групи блоків змішаної яскравості; тим самим 1-бітове кодове слово буде використовуватися тільки для найбільш ймовірних білих блоків. Дуже ефективною модифікацією даного способу є вибір розмірів блоку рівним . При цьому повністю білі рядки кодуються кодом 0, а всі інші рядки - кодом префікса 1, за яким слідує звичайна ПББ кодова послідовність. Інший підхід полягає в застосуванні ітеративного підходу, відповідно з яким двійкове зображення або бітова площина розбивається на послідовність зменшуваних двовимірних підблоків. Цілком білі блоки отримують код 0, а всі інші діляться на підблоки з префіксом 1 і кодуються аналогічним чином. Таким чином, якщо подблоков є цілком білим, то він є префіксом 1, що вказує, що це підблоки першого рівня, за яким, котрим слід 0, що вказує, що подблоков білий. Якщо ж подблоков не є цілком білим, то процес розбиття продовжується до тих пір, поки не буде досягнутий заданий поріг, після чого подблоков кодується або кодом 0, якщо він цілком білий, або кодом 1, за яким йде зображення підблока.

Одномірне кодування довжин серій

Ефективною альтернативою кодуванню областей сталості, є уявлення кожного рядка зображення або бітової площини послідовністі довжин, яка описує протяг сусідніх чорних або білих пікселів. Цей метод, що відноситься до кодування довжин серій (КДС), був розроблений в 1950-х роках і разом зі своїм двовимірних розширенням став стандартним методом стиснення у факсимільному (ФАКС) кодуванні. Основна ідея полягає в тому, що при скануванні рядки зліва направо виявляються неперервні серії з нулів або одиниць, які потім кодуються кодом їх довжини; крім того, встановлюються домовленість про визначення значення кожної серії. Найбільш частими методами завдання значення серії є наступні: (1) задавати значення першої серії кожного рядка, або (2) постановити, що кожен рядок починається з білої серії, однак допустити, що її довжина може бути нульовою.

Хоча кодування довжин серій саме по собі є досить ефективним методом стиснення зображень (див. приклад у Розділі 1.1.2), зазвичай можна додатково підвищити ступінь стиснення шляхом нерівномірного кодування самих значень довжин серій. До того ж, довжини чорних і білих серій можуть кодуватися окремо, використовуючи різні нерівномірні коди, кожен їх яких оптимізований по своїй статистиці. Наприклад, допускаючи, що символ представляе чорну серію довжини , можна оцінити ймовірність того, що символ  може бути породжений гіпотетичним джерелом довжин чорних серій, шляхом ділення числа чорних серій дліни зображення на загальне число чорних серій. Оцінка ентропії цього джерела довжин чорних серій, що позначається , виходить підстановкою цих ймовірностей в (1.3-3). Аналогічним чином можна підрахувати ентропію джерела довжин білих серій, що позначається . Наближене значення загальної ентропії зображення, кодованого довжинами серій, складе

де означають середні значення довжин чорних і білих серій. Формула (1.4-4) дає оцінку середнього числа бітів на піксель, що потрібні для стиснення двійкового зображення кодом довжин серій.

Двовимірне кодування довжин серій

Концепції одновимірного кодування довжин серій легко розширюються на побудову різних варіантів двовимірного кодування. Одним з найбільш відомих способів є кодування відносних адрес (КВА), засноване на відстеженні двійкових переходів, які починають і закінчують кожну серію із чорних або білих елементів. Рис. 1.17 (а) ілюструє одну з реалізацій такого підходу. Нехай ес є відстань від поточного переходу с до попереднього переходу е (протилежного знака) на тому ж рядку, а сс' є відстань від с до першого аналогічного (тобто того ж знака) пе ¬ рехода на попередньому рядку після е , який позначається с'. Якщо  ес<сс', то кодуються КОА відстань d буде дорівнює ес, якщо сс'<ес, то d встановлюється рівним сс'.

а)

б)

1.17. Ілюстрація кодування відносних адрес (КВА).

Подібно кодуванню довжин серій, кодування відносних адрес також вимагає ухвалення угоди про визначення значень серій. Крім того, для коректної роботи на кордонах зображення, передбачається наявність фіктивних переходів на початку і наприкінці кожного рядка, так само як і фіктивної передує початкового рядка (скажімо, цілком білою). Нарешті, оскільки для більшості реальних зображень розподіл ймовірностей КВА відстаней є нерівномірним (див. Розділ 1.1.1), заключним кроком процесу КВА буде кодування вибраного (тобто найкоротшого) КВА відстані d за допомогою підходящого нерівномірного кода. Як показано на Рис. 1.17 (6), може бути використаний код, подібний -коду. Найменшим відстаням присвоюються найкоротші кодові слова, а всі інші відстані кодуються з використанням префіксів. Код префікса встановлює діапазон для значення d, а наступне за ним значення (позначене ххх ... х на Рис. 1.17 (6)) - зсув d щодо початкової межі діапазону. Якщо ес і сс'дорівнюють +8 і +4, як показано на 1.17 (а), то правильний КВА код буде 1100011. Нарешті, якщо d = 0, то з знаходиться безпосередньо під с', тоді як якщо d = 1, то декодер має можливість вибрати найблищу точку переходу, оскільки код 100 не розрізняє, вказується чи зсув щодо поточної або попереднього рядка.

Простежування і кодування контурів

Кодування відносних адрес - всього лише один з можливих підходів для представлення яскравості переходів, формують контури на двійковому зображенні. Іншим підходом є представлення кожного контуру за допомогою набору граничних точок, або однієї граничної точкою і набором напрямних. Останній метод іноді називають прямим простежуванням контурів. У даному розділі буде розглянутий ще один метод, що називається диференціальне кодоване з пророкуванням (ДКП), який відображає найважливіші характеристики обох підходів. Він являє собою порядкову процедуру простежування контурів.

У диференціальному кодуванні з пророкуванням передній і задній контури кожного об'єкта зображення (див. Рис. 1.18) простежуються одночасно, щоб сформувати послідовність пар ( , ). Величина означає різницю між координатами переднього контуру сусідніх рядків, а - різниця між довжиною об'єкта на сусідніх рядках. Ці різниці, а також спеціальні повідомлення, що вказують на початок нового контуру (повідомлення початок нового контуру) і закінчення старого контуру (повідомлення замикання контуру), описують кожний об'єкт.

 

Рис. 1.18. Параметри алгоритму диференціального кодування з пророкуванням (ДКП).

Якщо замінюється різницею між координатами задніх контурів об'єкта на сусідніх рядках, позначеної , то метод називається двойним дельта кодуванням (ДЦК).

Повідомлення про початок і замиканні контуру дозволяють парам ( , ) або ( , ), породженим на якійсь одній рядку зображення, бути правильно пов'язаними з відповідними парами на попередній і подальших рядках. Без цих повідомлень декодер не зміг би зв'язати одну пару різниць з іншого, або правильно розмістити контур на зображенні. Щоб уникнути кодування координат стовпця і рядка в кожному повідомленні про початок і замиканні контура, часто використовують окремий код, що дозволяє ідентифікувати рядки, взагалі не містять точок об'єктів. Фінальним кроком як ДКП-, так і ДДК-кодування є кодування значень , або , а також координат початку і замикання контурів підходящим нерівномірним кодом.

Приклад 1.14. Порівняння методів стиснення двійкових зображень.

Закінчуючи цей розділ, порівняємо вищеописані методи стиснення двійкових зображень. Методи порівнюються шляхом стиснення зображень на Рис. 1.14. Підсумкові швидкості кодів і коеффіціентів стиснення представлені в Таблицях 1.8 та 1.9. Відзначимо, що результати для довжин серій в методі КДС, а також для відстаней в методах ДКП та ДДК, наведені з урахуванням стиснення, досяжного при послідовному нерівномірному кодуванні (див. Розділі 1.4.1). Для цього визначались і використовувалися оцінки першого порядку ентропії (див. Розділ 1.3.4).

Результати, представлені в Таблицях 1.8 та 1.9, демонструють, що всі методи здатні скорочувати деяку кількість межелемент-ної надмірності. Тобто, результуючі кодові швидкості є нижче, ніж оцінка першого порядку ентропії кожного зображення.

Таблиця 1.8. Результати стиснення без втрат зображення на Рис. 1.14 (а) методом кодування бітових площин (прочерк у графі таблиці означає відсутність стиснення, швидкість коду дорівнює 1,00): Н = 6,82 біта/піксель.

Таблиця 1.9. Результати стиснення без втрат двійкового зображення на Рис. 1.14 (б): Н = 0,55 біта/піксель.

Метод кодування довжин серій виявляється найкращим при кодування многоградаціонного зображення за допомогою бітових площин, в той час як двовимірні методи, такі як ДКП, ДДК та КОА, забезпечують більш гарне стиснення двухградаціонного зображення. Більш того, відносно проста процедура використання коду Грея при стисненні зображення на Рис. 1.14 (а), дозволяє поліпшити отриману ефективність кодування приблизно на 1 біт/піксель. Накінець, зауважимо, що всі п'ять методів стиснення змогли стиснути напівтонове зображення тільки з коефіцієнтами стиснення від 1 до 2, у той час як при стисненні двійкового зображення на Рис. 1.14 (6) їм вдалося досягти коефіцієнти стиску від 2 до 5. Як видно з Таблиці 1.8, причина різниці в ефективності полягає в тому, що всі алгоритми виявилися нездатними стиснути зображення молодших порядків при кодуванні зображення по бітових площинах. Прочерком у графах таблиці позначені ті випадки, коли застосування алгоритму стиснення приводь до збільшення обсягу даних. У таких випадках для подання бітової площині використовувалися незжаті дані, і отже, до швидкості коду додавалася величина 1 біт/піксель.