|
Последовательность действительных
чисел – функция f(n)
определенная на множестве N
всех натуральных чисел. Число f(n)
– n-ый член последовательности
xn
(xn=f(n))
– формула общего члена
последовательности (nϵN).
Пример – (n2):
12, 22… n2.
Последовательности xn
– ограниченная, если существует
М>0, что для любого n из
N выполняется |xn|<=M.
Xn
– возрастающая, если выполняется
xn+1>=xn.
Такие последовательности – монотонные.
Если все члены последовательности =
одному и тому же числу с – постоянная.
 .
Если для любого числа ε>0 существует
N(ε), что
при всех n из N
выполняется |xn-a|<ε,
а последовательность – сходящаяся.
Из этого получаем a-ε<xn<a+ε.
Интервал (a+ε; a-ε)
– ε-окрестность точки
а. Геометрический смысл – а
является пределом последовательности,
если в любой его окрестности есть
почти все ее члены. Сходящаяся
последовательность имеет только 1
предел. Последовательность без предела
– расходящаяся. Постоянная
последовательность = с имеет предел .
Если для любого числа ε>0 существует
N(ε), что
при всех n из N
выполняется |xn-a|<ε,
а последовательность – сходящаяся.
Из этого получаем a-ε<xn<a+ε.
Интервал (a+ε; a-ε)
– ε-окрестность точки
а. Геометрический смысл – а
является пределом последовательности,
если в любой его окрестности есть
почти все ее члены. Сходящаяся
последовательность имеет только 1
предел. Последовательность без предела
– расходящаяся. Постоянная
последовательность = с имеет предел
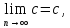 т.к.
|xn-c|=|c-c|=0<ε.
Теорема Вейерштрасса – всякая
монотонная ограниченная последовательность
имеет предел, например хn=(1+ т.к.
|xn-c|=|c-c|=0<ε.
Теорема Вейерштрасса – всякая
монотонная ограниченная последовательность
имеет предел, например хn=(1+ )n,
nϵN, предел
которой )n,
nϵN, предел
которой
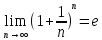 .
Число е – неперово число
=2,718281…, принято за основание
натурального логарифма - .
Число е – неперово число
=2,718281…, принято за основание
натурального логарифма -

|
|
Предел функции числа А в точке
х0 – для
любого положительного ε есть
положительное число ∆, что для всех
x≠x0,
удовлетворяющих |x-x0|<∆
выполняется |f(x)-A|<ε
=
 .
∆ зависит от ε. Число А1 – предел
функции y=f(x)
слева в точке x0,
если для любого положительного
ε есть положительное число ∆ такое,
что при хϵ(х0-∆; х0) выполняется
|f(x) –
A1|<ε – .
∆ зависит от ε. Число А1 – предел
функции y=f(x)
слева в точке x0,
если для любого положительного
ε есть положительное число ∆ такое,
что при хϵ(х0-∆; х0) выполняется
|f(x) –
A1|<ε –
 .
Точно также и с пределом функции справа
от х0. Пределы справа и слева –
односторонние пределы. Если
существует .
Точно также и с пределом функции справа
от х0. Пределы справа и слева –
односторонние пределы. Если
существует
 ,
то есть оба односторонних предела
A=A1=A2.
Если А1≠А2, то предел не
существует. Пусть y=f(x)
определена на всей числовой прямой
(-∞; +∞). Число А – предел функции
при х ,
то есть оба односторонних предела
A=A1=A2.
Если А1≠А2, то предел не
существует. Пусть y=f(x)
определена на всей числовой прямой
(-∞; +∞). Число А – предел функции
при х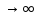 ,
если для любого ε>0 есть такое
положительное число М=М(ε), что при
всех х удовлетворяющих |x|>M
выполняется |f(x)-A|<ε
– ,
если для любого ε>0 есть такое
положительное число М=М(ε), что при
всех х удовлетворяющих |x|>M
выполняется |f(x)-A|<ε
–
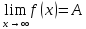
|
|
Бесконечно малая
y=f(x)
– при x ,
если ,
если
 .
Обозначаются α,β… Пример y=x4
при х .
Обозначаются α,β… Пример y=x4
при х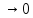 ,
y=x+5 при
х ,
y=x+5 при
х .
Теорема – Алгебраическая
сумма конечного числа б.м. функции
есть б.м. Есть 2 б.м. α(х) и β(х) при .
Теорема – Алгебраическая
сумма конечного числа б.м. функции
есть б.м. Есть 2 б.м. α(х) и β(х) при
 ,
значит ,
значит
 .
Для любого ε>0 и ε/2 есть ∆>0, что для
всех х удовлетворяющих 0<|x-x0|<∆
выполняется |α(x)|<ε/2.
Также и для β(х). Имеет место соотношение
|α(x)+β(x)|<ε/2+ε/2=ε.
Таким образом .
Для любого ε>0 и ε/2 есть ∆>0, что для
всех х удовлетворяющих 0<|x-x0|<∆
выполняется |α(x)|<ε/2.
Также и для β(х). Имеет место соотношение
|α(x)+β(x)|<ε/2+ε/2=ε.
Таким образом
 Теорема – Произведение
ограниченной функции на б.м. функцию
– есть функция б.м. Следствие:
произведение б.м. на число – есть б.м.
и т.к. б.м. ограничена, то произведение
2-х б.м. есть б.м. Теорема – Частное
от деления б.м. на функцию, имеющую ≠0
предел – есть б.м.
Теорема – Произведение
ограниченной функции на б.м. функцию
– есть функция б.м. Следствие:
произведение б.м. на число – есть б.м.
и т.к. б.м. ограничена, то произведение
2-х б.м. есть б.м. Теорема – Частное
от деления б.м. на функцию, имеющую ≠0
предел – есть б.м.
Бесконечно большая y=f(x)
– при x ,
если для любого M>0 есть
∆>0 зависящее от M, что
для всех х=0<|x-x0|<∆
выполняется |f(x)|>M.
Пример y=3x
при х ,
если для любого M>0 есть
∆>0 зависящее от M, что
для всех х=0<|x-x0|<∆
выполняется |f(x)|>M.
Пример y=3x
при х .
Б.М. и Б.Б. тесно связаны. Теорема
– Если α(x)
– б.м. (α≠0), то
1/α(х) – б.б. и наоборот. Пусть α(х) –
б.м. при x .
Б.М. и Б.Б. тесно связаны. Теорема
– Если α(x)
– б.м. (α≠0), то
1/α(х) – б.б. и наоборот. Пусть α(х) –
б.м. при x ,
тогда | ,
тогда | ,
значит ,
значит
 – б.б. Аналогично и обратное утверждение.
Все док-ва теорем работают и для случая
когда
– б.б. Аналогично и обратное утверждение.
Все док-ва теорем работают и для случая
когда
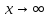
|
|
Теорема 1 – Если f(x)
имеет предел =А то ее можно представить
как сумму числа А и б.м. α(х), т.е. если
 ,
то f(x)=A+α(x).
Теорема 2 обратная Теореме 1. Во
всех этих теоремах пределы существуют
и х может стремится как к х0, так
и к ∞. Теорема 3 – предел суммы
(разности) 2-х функций = сумме (разности)
их пределов: ,
то f(x)=A+α(x).
Теорема 2 обратная Теореме 1. Во
всех этих теоремах пределы существуют
и х может стремится как к х0, так
и к ∞. Теорема 3 – предел суммы
(разности) 2-х функций = сумме (разности)
их пределов:
 .
Пусть .
Пусть
 ,
тогда по теореме 1 – f(x)=A+α(x)
и ϕ(x)=B+β(x),
где α(х) и β(х) – б.м. при x ,
тогда по теореме 1 – f(x)=A+α(x)
и ϕ(x)=B+β(x),
где α(х) и β(х) – б.м. при x .
Тогда f(x)+ϕ(x)=A+α(x)+B+β(x).
Сумма α(x)
и β(х) – б.м., тогда по теореме 2 число
А+В – предел f(x)+ϕ(x),
т.е. .
Тогда f(x)+ϕ(x)=A+α(x)+B+β(x).
Сумма α(x)
и β(х) – б.м., тогда по теореме 2 число
А+В – предел f(x)+ϕ(x),
т.е.
 .
В случае разности все аналогично.
Теорема 4 – Предел произведения
2-х функций = произведению их пределов: .
В случае разности все аналогично.
Теорема 4 – Предел произведения
2-х функций = произведению их пределов:
 .
В частности .
В частности
 .
Постоянный множитель можно выносить
за знак предела. Теорема 5 – Предел
дроби = пределу числителя деленному
на предел знаменателя, если предел
знаменателя ≠0. Теорема 6 (о пределе
промежуточной функции) – если
f(x) заключена
между 2-мя функциями ϕ(х) и g(х) .
Постоянный множитель можно выносить
за знак предела. Теорема 5 – Предел
дроби = пределу числителя деленному
на предел знаменателя, если предел
знаменателя ≠0. Теорема 6 (о пределе
промежуточной функции) – если
f(x) заключена
между 2-мя функциями ϕ(х) и g(х)
 к одному пределу, то она также
к одному пределу, то она также
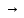 к этому пределу, т.е.
к этому пределу, т.е.

|
|
1-ый замечательный предел –
 .
2-ой замечательный предел – .
2-ой замечательный предел –
 ,
если положить 1/х=α (α ,
если положить 1/х=α (α 0
при х 0
при х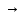 ∞) ∞)
|
|
2 б.м. функции
сравниваются с помощью отношения.
Сумма, разность и произведение б. м. –
есть б.м. Отношения бывают – конечным
числом, б.б., б.м. или не стремиться ни
к какому пределу. Пусть 𝛼(𝑥)и
𝛽(𝑥)
− 2 б. м. (т.е.
 ):
1) Если ):
1) Если
 б.м. 1-го порядка. Если с=1, то
б.м. 1-го порядка. Если с=1, то
 эквивалентные б.м. 2) Если
эквивалентные б.м. 2) Если
 ,
то α(х) б.м. более высокого порядка,
чем β(х). 3) Если ,
то α(х) б.м. более высокого порядка,
чем β(х). 3) Если
 ,
то α(х) б.м. более низкого порядка.
4) Если ,
то α(х) б.м. более низкого порядка.
4) Если
 не существует, то
не существует, то
 несравнимые б.м. Таковы сравнения
б.м. при 𝑥→𝑥0≠0,
𝑥→±∞. Теорема
– Предел отношения 2-х б.м. не
изменится, если каждую или 1 из них
заменить эквивалентной ей б.м. 1)
несравнимые б.м. Таковы сравнения
б.м. при 𝑥→𝑥0≠0,
𝑥→±∞. Теорема
– Предел отношения 2-х б.м. не
изменится, если каждую или 1 из них
заменить эквивалентной ей б.м. 1) .
При x .
При x 0 0
|
|
y=f(x)
непрерывная в точке х0:
1) f(x)
– определена в точке х0 и ее
окрестности 2) существует предел при
х х0
3) предел при х х0
3) предел при х х0
= значению функции в точке х0.
Следствие х0
= значению функции в точке х0.
Следствие
 – при нахождении предела непрерывной
функции можно переходить к пределу
под знаком функции. Если
– при нахождении предела непрерывной
функции можно переходить к пределу
под знаком функции. Если то f(x)
непрерывна справа от 0. Аналогично и
слева. Пусть f(x) определена на некотором
интервале (а,b). Возьмём произвольную
точку 𝑥0∈(𝑎,𝑏)
для любого 𝑥∈(𝑎,𝑏)
разность 𝑥−𝑥0
– приращение аргумента x в точке 𝑥0,
обозначается ∆𝑥.
Отсюда 𝒙-𝒙0=∆𝒙.
Разность соответствующих значений
𝑓(𝑥)−𝑓(𝑥0)−приращение
f(x) в точке
𝑥0 и
обозначается ∆𝑦=𝑓(𝑥)−𝑓(𝑥0),
значит ∆𝒚=𝒇(𝒙0+∆𝒙)−𝒇(𝒙0),
значит,
то f(x)
непрерывна справа от 0. Аналогично и
слева. Пусть f(x) определена на некотором
интервале (а,b). Возьмём произвольную
точку 𝑥0∈(𝑎,𝑏)
для любого 𝑥∈(𝑎,𝑏)
разность 𝑥−𝑥0
– приращение аргумента x в точке 𝑥0,
обозначается ∆𝑥.
Отсюда 𝒙-𝒙0=∆𝒙.
Разность соответствующих значений
𝑓(𝑥)−𝑓(𝑥0)−приращение
f(x) в точке
𝑥0 и
обозначается ∆𝑦=𝑓(𝑥)−𝑓(𝑥0),
значит ∆𝒚=𝒇(𝒙0+∆𝒙)−𝒇(𝒙0),
значит, =𝟎
или =𝟎
или
 .
y=f(x)
непрерывна в точке х0,
если она определена в данной точке
и ее окрестности, и выполняется
предыдущее равенство, т.е. б.м. значению
∆х соответствует б.м. приращение ∆у.
y=f(x)
– непрерывна на отрезке [a,b] если она
определена на интервале (𝑎,𝑏)
и непрерывна слева в точке а и справа
в точке b. Точка 𝒙0
− точка разрыва y=f(x), если
она принадлежит области определения
f(x) или её
границе и не является точкой
непрерывности. 𝒙0
– точка разрыва 1-го рода,
если в этой точке существуют конечные
пределы справа и слева, т.е. .
y=f(x)
непрерывна в точке х0,
если она определена в данной точке
и ее окрестности, и выполняется
предыдущее равенство, т.е. б.м. значению
∆х соответствует б.м. приращение ∆у.
y=f(x)
– непрерывна на отрезке [a,b] если она
определена на интервале (𝑎,𝑏)
и непрерывна слева в точке а и справа
в точке b. Точка 𝒙0
− точка разрыва y=f(x), если
она принадлежит области определения
f(x) или её
границе и не является точкой
непрерывности. 𝒙0
– точка разрыва 1-го рода,
если в этой точке существуют конечные
пределы справа и слева, т.е.
 .
При этом: 1) Если А1=А2,
то точка 𝑥0
– точка устранимого разрыва;
2) Если А1≠А2, то точка 𝑥0
– точка неустранимого разрыва.
|А1−А2| - скачок f(x)
в точке разрыва 1-ого порядка. 𝒙0
– точка разрыва 2-ого порядка,
если хотя бы 1 из односторонних пределов
не существует или = ∞ .
При этом: 1) Если А1=А2,
то точка 𝑥0
– точка устранимого разрыва;
2) Если А1≠А2, то точка 𝑥0
– точка неустранимого разрыва.
|А1−А2| - скачок f(x)
в точке разрыва 1-ого порядка. 𝒙0
– точка разрыва 2-ого порядка,
если хотя бы 1 из односторонних пределов
не существует или = ∞
|
|
Теорема – Пусть функции f(x)
и g(x) непрерывны в точке х0, тогда
f(x)±g(x); f(x)∗g(x);
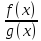 (g(x)≠0) так
же непрерывны в этой точке. Справедлива
для любого конечного числа слагаемых
или сомножителей.
(g(x)≠0) так
же непрерывны в этой точке. Справедлива
для любого конечного числа слагаемых
или сомножителей.
|
|
Теорема (1-ая теорема
Больцано-Коши) – Пусть f(x) непрерывна
на отрезке [a,b] и на концах имеет значение
разных знаков, тогда существует точка
𝐶∈(𝑎,𝑏),
в которой значение 𝑓(𝑐)=0.
Геометрический смысл: непрерывная
кривая при переходе с одной полуплоскости,
по отношению к оси, на другую, пересекает
эту ось. Теорема (2-ая теорема
Больцано-Коши) – Пусть f(x) непрерывна
на отрезке [a,b], причём f(a)=A, f(b) = B. Пусть
далее С – число (любое), заключённое
между А и В, тогда на отрезке [a,b] найдётся
такая точка с , что значение f(x)
в этой точке равно C – f(С)=C (Другими
словами: непрерывная f(x)
при переходе от одного значения к
другому принимает и все промежуточные
значения). Теорема (1-ая теорема
Вейерштрасса) – Если f(x) определена
и непрерывна на отрезке [a,b], то она
ограничена на этом отрезке.
Геометрический смысл: график f(x)
не выходит из полосы, ограниченной
y=-M, y=M. Теорема становится неверной,
если в ней отрезок [a,b] заменить
интервалом (a,b). Теорема (2-ая теорема
Вейерштрасса) - Если f(x) непрерывна
на отрезке [a,b], то она достигает на
этом отрезке своё наибольшее и
наименьшее значения. f(x)<=f(x1)=M
(max) и f(x)<=f(x2)=m
(min)
|


 .
Если для любого числа ε>0 существует
N(ε), что
при всех n из N
выполняется |xn-a|<ε,
а последовательность – сходящаяся.
Из этого получаем a-ε<xn<a+ε.
Интервал (a+ε; a-ε)
– ε-окрестность точки
а. Геометрический смысл – а
является пределом последовательности,
если в любой его окрестности есть
почти все ее члены. Сходящаяся
последовательность имеет только 1
предел. Последовательность без предела
– расходящаяся. Постоянная
последовательность = с имеет предел
.
Если для любого числа ε>0 существует
N(ε), что
при всех n из N
выполняется |xn-a|<ε,
а последовательность – сходящаяся.
Из этого получаем a-ε<xn<a+ε.
Интервал (a+ε; a-ε)
– ε-окрестность точки
а. Геометрический смысл – а
является пределом последовательности,
если в любой его окрестности есть
почти все ее члены. Сходящаяся
последовательность имеет только 1
предел. Последовательность без предела
– расходящаяся. Постоянная
последовательность = с имеет предел
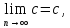 т.к.
|xn-c|=|c-c|=0<ε.
Теорема Вейерштрасса – всякая
монотонная ограниченная последовательность
имеет предел, например хn=(1+
т.к.
|xn-c|=|c-c|=0<ε.
Теорема Вейерштрасса – всякая
монотонная ограниченная последовательность
имеет предел, например хn=(1+ )n,
nϵN, предел
которой
)n,
nϵN, предел
которой
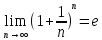 .
Число е – неперово число
=2,718281…, принято за основание
натурального логарифма -
.
Число е – неперово число
=2,718281…, принято за основание
натурального логарифма -

 .
∆ зависит от ε. Число А1 – предел
функции y=f(x)
слева в точке x0,
если для любого положительного
ε есть положительное число ∆ такое,
что при хϵ(х0-∆; х0) выполняется
|f(x) –
A1|<ε –
.
∆ зависит от ε. Число А1 – предел
функции y=f(x)
слева в точке x0,
если для любого положительного
ε есть положительное число ∆ такое,
что при хϵ(х0-∆; х0) выполняется
|f(x) –
A1|<ε –
 .
Точно также и с пределом функции справа
от х0. Пределы справа и слева –
односторонние пределы. Если
существует
.
Точно также и с пределом функции справа
от х0. Пределы справа и слева –
односторонние пределы. Если
существует
 ,
то есть оба односторонних предела
A=A1=A2.
Если А1≠А2, то предел не
существует. Пусть y=f(x)
определена на всей числовой прямой
(-∞; +∞). Число А – предел функции
при х
,
то есть оба односторонних предела
A=A1=A2.
Если А1≠А2, то предел не
существует. Пусть y=f(x)
определена на всей числовой прямой
(-∞; +∞). Число А – предел функции
при х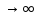 ,
если для любого ε>0 есть такое
положительное число М=М(ε), что при
всех х удовлетворяющих |x|>M
выполняется |f(x)-A|<ε
–
,
если для любого ε>0 есть такое
положительное число М=М(ε), что при
всех х удовлетворяющих |x|>M
выполняется |f(x)-A|<ε
–
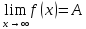
 ,
если
,
если
 .
Обозначаются α,β… Пример y=x4
при х
.
Обозначаются α,β… Пример y=x4
при х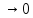 ,
y=x+5 при
х
,
y=x+5 при
х .
Теорема – Алгебраическая
сумма конечного числа б.м. функции
есть б.м. Есть 2 б.м. α(х) и β(х) при
.
Теорема – Алгебраическая
сумма конечного числа б.м. функции
есть б.м. Есть 2 б.м. α(х) и β(х) при
 ,
значит
,
значит
 .
Для любого ε>0 и ε/2 есть ∆>0, что для
всех х удовлетворяющих 0<|x-x0|<∆
выполняется |α(x)|<ε/2.
Также и для β(х). Имеет место соотношение
|α(x)+β(x)|<ε/2+ε/2=ε.
Таким образом
.
Для любого ε>0 и ε/2 есть ∆>0, что для
всех х удовлетворяющих 0<|x-x0|<∆
выполняется |α(x)|<ε/2.
Также и для β(х). Имеет место соотношение
|α(x)+β(x)|<ε/2+ε/2=ε.
Таким образом
 Теорема – Произведение
ограниченной функции на б.м. функцию
– есть функция б.м. Следствие:
произведение б.м. на число – есть б.м.
и т.к. б.м. ограничена, то произведение
2-х б.м. есть б.м. Теорема – Частное
от деления б.м. на функцию, имеющую ≠0
предел – есть б.м.
Теорема – Произведение
ограниченной функции на б.м. функцию
– есть функция б.м. Следствие:
произведение б.м. на число – есть б.м.
и т.к. б.м. ограничена, то произведение
2-х б.м. есть б.м. Теорема – Частное
от деления б.м. на функцию, имеющую ≠0
предел – есть б.м. ,
если для любого M>0 есть
∆>0 зависящее от M, что
для всех х=0<|x-x0|<∆
выполняется |f(x)|>M.
Пример y=3x
при х
,
если для любого M>0 есть
∆>0 зависящее от M, что
для всех х=0<|x-x0|<∆
выполняется |f(x)|>M.
Пример y=3x
при х .
Б.М. и Б.Б. тесно связаны. Теорема
– Если α(x)
– б.м. (α≠0), то
1/α(х) – б.б. и наоборот. Пусть α(х) –
б.м. при x
.
Б.М. и Б.Б. тесно связаны. Теорема
– Если α(x)
– б.м. (α≠0), то
1/α(х) – б.б. и наоборот. Пусть α(х) –
б.м. при x ,
тогда |
,
тогда | ,
значит
,
значит
 – б.б. Аналогично и обратное утверждение.
Все док-ва теорем работают и для случая
когда
– б.б. Аналогично и обратное утверждение.
Все док-ва теорем работают и для случая
когда
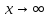
 ,
то f(x)=A+α(x).
Теорема 2 обратная Теореме 1. Во
всех этих теоремах пределы существуют
и х может стремится как к х0, так
и к ∞. Теорема 3 – предел суммы
(разности) 2-х функций = сумме (разности)
их пределов:
,
то f(x)=A+α(x).
Теорема 2 обратная Теореме 1. Во
всех этих теоремах пределы существуют
и х может стремится как к х0, так
и к ∞. Теорема 3 – предел суммы
(разности) 2-х функций = сумме (разности)
их пределов:
 .
Пусть
.
Пусть
 ,
тогда по теореме 1 – f(x)=A+α(x)
и ϕ(x)=B+β(x),
где α(х) и β(х) – б.м. при x
,
тогда по теореме 1 – f(x)=A+α(x)
и ϕ(x)=B+β(x),
где α(х) и β(х) – б.м. при x .
Тогда f(x)+ϕ(x)=A+α(x)+B+β(x).
Сумма α(x)
и β(х) – б.м., тогда по теореме 2 число
А+В – предел f(x)+ϕ(x),
т.е.
.
Тогда f(x)+ϕ(x)=A+α(x)+B+β(x).
Сумма α(x)
и β(х) – б.м., тогда по теореме 2 число
А+В – предел f(x)+ϕ(x),
т.е.
 .
В случае разности все аналогично.
Теорема 4 – Предел произведения
2-х функций = произведению их пределов:
.
В случае разности все аналогично.
Теорема 4 – Предел произведения
2-х функций = произведению их пределов:
 .
В частности
.
В частности
 .
Постоянный множитель можно выносить
за знак предела. Теорема 5 – Предел
дроби = пределу числителя деленному
на предел знаменателя, если предел
знаменателя ≠0. Теорема 6 (о пределе
промежуточной функции) – если
f(x) заключена
между 2-мя функциями ϕ(х) и g(х)
.
Постоянный множитель можно выносить
за знак предела. Теорема 5 – Предел
дроби = пределу числителя деленному
на предел знаменателя, если предел
знаменателя ≠0. Теорема 6 (о пределе
промежуточной функции) – если
f(x) заключена
между 2-мя функциями ϕ(х) и g(х)
 к одному пределу, то она также
к одному пределу, то она также
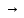 к этому пределу, т.е.
к этому пределу, т.е.

 .
2-ой замечательный предел –
.
2-ой замечательный предел –
 ,
если положить 1/х=α (α
,
если положить 1/х=α (α 0
при х
0
при х ∞)
∞) ):
1) Если
):
1) Если
 б.м. 1-го порядка. Если с=1, то
б.м. 1-го порядка. Если с=1, то
 эквивалентные б.м. 2) Если
эквивалентные б.м. 2) Если
 ,
то α(х) б.м. более высокого порядка,
чем β(х). 3) Если
,
то α(х) б.м. более высокого порядка,
чем β(х). 3) Если
 ,
то α(х) б.м. более низкого порядка.
4) Если
,
то α(х) б.м. более низкого порядка.
4) Если
 не существует, то
не существует, то
 несравнимые б.м. Таковы сравнения
б.м. при 𝑥→𝑥0≠0,
𝑥→±∞. Теорема
– Предел отношения 2-х б.м. не
изменится, если каждую или 1 из них
заменить эквивалентной ей б.м. 1)
несравнимые б.м. Таковы сравнения
б.м. при 𝑥→𝑥0≠0,
𝑥→±∞. Теорема
– Предел отношения 2-х б.м. не
изменится, если каждую или 1 из них
заменить эквивалентной ей б.м. 1) .
При x
.
При x 0
0 х0
3) предел при х
х0
3) предел при х х0
= значению функции в точке х0.
Следствие
х0
= значению функции в точке х0.
Следствие
 – при нахождении предела непрерывной
функции можно переходить к пределу
под знаком функции. Если
– при нахождении предела непрерывной
функции можно переходить к пределу
под знаком функции. Если то f(x)
непрерывна справа от 0. Аналогично и
слева. Пусть f(x) определена на некотором
интервале (а,b). Возьмём произвольную
точку 𝑥0∈(𝑎,𝑏)
для любого 𝑥∈(𝑎,𝑏)
разность 𝑥−𝑥0
– приращение аргумента x в точке 𝑥0,
обозначается ∆𝑥.
Отсюда 𝒙-𝒙0=∆𝒙.
Разность соответствующих значений
𝑓(𝑥)−𝑓(𝑥0)−приращение
f(x) в точке
𝑥0 и
обозначается ∆𝑦=𝑓(𝑥)−𝑓(𝑥0),
значит ∆𝒚=𝒇(𝒙0+∆𝒙)−𝒇(𝒙0),
значит,
то f(x)
непрерывна справа от 0. Аналогично и
слева. Пусть f(x) определена на некотором
интервале (а,b). Возьмём произвольную
точку 𝑥0∈(𝑎,𝑏)
для любого 𝑥∈(𝑎,𝑏)
разность 𝑥−𝑥0
– приращение аргумента x в точке 𝑥0,
обозначается ∆𝑥.
Отсюда 𝒙-𝒙0=∆𝒙.
Разность соответствующих значений
𝑓(𝑥)−𝑓(𝑥0)−приращение
f(x) в точке
𝑥0 и
обозначается ∆𝑦=𝑓(𝑥)−𝑓(𝑥0),
значит ∆𝒚=𝒇(𝒙0+∆𝒙)−𝒇(𝒙0),
значит, =𝟎
или
=𝟎
или
 .
y=f(x)
непрерывна в точке х0,
если она определена в данной точке
и ее окрестности, и выполняется
предыдущее равенство, т.е. б.м. значению
∆х соответствует б.м. приращение ∆у.
y=f(x)
– непрерывна на отрезке [a,b] если она
определена на интервале (𝑎,𝑏)
и непрерывна слева в точке а и справа
в точке b. Точка 𝒙0
− точка разрыва y=f(x), если
она принадлежит области определения
f(x) или её
границе и не является точкой
непрерывности. 𝒙0
– точка разрыва 1-го рода,
если в этой точке существуют конечные
пределы справа и слева, т.е.
.
y=f(x)
непрерывна в точке х0,
если она определена в данной точке
и ее окрестности, и выполняется
предыдущее равенство, т.е. б.м. значению
∆х соответствует б.м. приращение ∆у.
y=f(x)
– непрерывна на отрезке [a,b] если она
определена на интервале (𝑎,𝑏)
и непрерывна слева в точке а и справа
в точке b. Точка 𝒙0
− точка разрыва y=f(x), если
она принадлежит области определения
f(x) или её
границе и не является точкой
непрерывности. 𝒙0
– точка разрыва 1-го рода,
если в этой точке существуют конечные
пределы справа и слева, т.е.
 .
При этом: 1) Если А1=А2,
то точка 𝑥0
– точка устранимого разрыва;
2) Если А1≠А2, то точка 𝑥0
– точка неустранимого разрыва.
|А1−А2| - скачок f(x)
в точке разрыва 1-ого порядка. 𝒙0
– точка разрыва 2-ого порядка,
если хотя бы 1 из односторонних пределов
не существует или = ∞
.
При этом: 1) Если А1=А2,
то точка 𝑥0
– точка устранимого разрыва;
2) Если А1≠А2, то точка 𝑥0
– точка неустранимого разрыва.
|А1−А2| - скачок f(x)
в точке разрыва 1-ого порядка. 𝒙0
– точка разрыва 2-ого порядка,
если хотя бы 1 из односторонних пределов
не существует или = ∞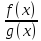 (g(x)≠0) так
же непрерывны в этой точке. Справедлива
для любого конечного числа слагаемых
или сомножителей.
(g(x)≠0) так
же непрерывны в этой точке. Справедлива
для любого конечного числа слагаемых
или сомножителей.