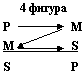1)Непосредственные умозаключения

Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным.

К непосредственным умозаключениям относятся: превращение, обращение, противопоставление предикату, умозаключение по «логическому квадрату».

Превращение - такое умозаключение, в котором исходное суждение преобразуется в новое суждение, противоположное по качеству, и с предикатом, противоречащим предикату исходного суждения.

Чтобы превратить суждение, надо изменить его связку на противоположную, а предикат - на противоречащее понятие. Если посылка выражена не в явной форме, то надо преобразовать ее в соответствии со схемами суждений А, Е, I, О.

Если посылка записана в форме суждения «Не все S суть Р» , то его надо преобразовать в частноотрицательное: «Некоторые S не суть Р».

Примеры и схемы превращения:

А:

Все студенты первого курса изучают логику.

Ни один студент первого курса не изучает не логику.

Схема:

Все S суть Р.

Ни одно S не суть не-Р.

 

Е: Ни одна кошка не является собакой.

Всякая кошка является не-собакой.

 

Ни один S не есть Р.

Все S есть не-Р.

 

I: Некоторые адвокаты суть спортсмены.

Некоторые адвокаты не суть не-спортсмены.

 

Некоторые S суть Р.

Некоторые S не суть не-Р.

 

О: Некоторые адвокаты не суть спортсмены.

Некоторые адвокаты суть не-спортсмены.

 

2)Простой Категорический силогизм

Являясь дедуктивным методом умозаключения, силлогизм строится из двух совместимых суждений, связанных общим понятием, обеспечивая объединение различных терминов в заключении и, позволяет дать заключение об отношении двух (крайних) понятий на основании их отношения к третьему (среднему). В ставшей уже привычной форме, их можно отобразить так:

В категорических силлогизмах участвуют категорические суждения, но, поскольку субъектно-предикатная структура в силлогизме меняется, то общее понятие, независимо от того, субъект оно или предикат, традиционно называют средним и обозначают буквой «M», а предикатом и субъектом считают понятия образовывающие субъект и предикат заключения.

Понятия, входящие в состав силлогизма называют его терминами. Большой термин – предикат заключения, посылка, его содержащая – большая посылка (пишется в первой строке силлогизма); Малый термин – субъект заключения, посылка его содержащая –малая посылка (пишется во второй строке); средний термин – общее звено посылок – общее понятие, объединяющее обе посылки (выпадающее в заключении):

Справедливость (P) предусматривает ответственность за поступки (M). Доброта (S) не требует ответственности (M) Доброта (S) несправедлива (P).

Положение среднего термина определяет четыре типа построения (фигуры) простого категорического силлогизма, каждый из которых должен соответствовать своему формальному правилу вывода:

	Большая посылка должна быть более общей, меньшая утвердительной. Ее формула (модус) последовательности посылок и следствия AAA, EAE, AII, EIO – любые другие комбинации ошибочны
	Большая посылка должна быть более общей и одна из посылок, а так же, заключение – отрицательным:AEE, AOO, EAE, EIO.
	Меньшая посылка должна быть утвердительной, а заключение – частным: AAI, EAO, IAI, OAO, AII, EIO.
	Не дает общеутвердительных заключений. Если большая посылка утвердительная, то меньшая должна быть общей. Если одна из посылок отрицательна, то обшей должна быть большая посылка: AAI, AEE, IAI, EAO, EIO.

Проверку правильности вывода легко провести, заменив смысловые значения символами (A, I, E, O) и определив тип фигуры. Так, суждение «Нечеткие и не лаконичные суждения не следуют логике в должной степени» можно представить в виде силлогизма:

AВся логика (P) является необходимой для правильной формулировки суждений (M). OНекоторые суждения (S) формулируются не вполне правильно (M) OНекоторые суждения (S) не вполне соответствует логике (P).

Где большая посылка общая (в данном случае, общеутвердительная), а другая (малая) и заключение – отрицательные (в данном случае частноотрицательные), из чего видно что, это умозаключение имеет структуру AOO и соответствует правилу второй фигуры. Таким образом, полученный вывод истинен.

Присутствующая в силлогизме поправка «не вполне» указывает на условность «правильной формулировки суждений», если бы существовал абсолютный критерий правильной формулировки, оговорка «не вполне» могла бы быть отброшена или заменена словом «абсолютно»

Кроме правил, касающихся формы фигур, для истинности вывода посредством простого категорического силлогизма, при его построении должны соблюдаться содержательные правила: