12. Паралелепіпед

Паралелепіпедом називається призма, в основі якої лежить паралелограм. Усі грані паралелепіпеда — паралелограми. Грані паралелепіпеда, які не мають спільних вершин, називаються протилежними.

Т1. Протилежні грані паралелепіпеда є паралельними й рівними.

Т2. Діагоналі паралелепіпеда перетинаються в одній точці й точкою перетину діляться навпіл.

Точка перетину діагоналей паралелепіпеда є його центром симетрії. У прямого паралелепіпеда є чотири діагоналі, які попарно дорівнюють одна одній.

Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом.

Усі грані прямокутного паралелепіпеда — прямокутники, які можна розбити на три пари рівних між собою. Довільну грань прямокутного паралелепіпеда можна вважати його основою. Враховуючи, що при паралельному проектуванні довільний паралелограм може зображуватися довільним паралелограмом, зо­браження прямокутного паралелепіпеда ніяк не відрізняється від зображеня будь-якого прямого паралелепіпеда.

Довжини непаралельних ребер називаються лінійними розмірами (вимірами) прямокутного паралелепіпеда.

Т3. У прямокутному паралелепіпеді всі діагоналі рівні. Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.

Усі двогранні кути прямокутного паралелепіпеда є прямими. Прямокутний паралелепіпед має три пари рівних між собою діагональних перерізів. Кожний із цих перерізів є прямокутником.

Кожна пара перерізів перетинається по прямій, яка проходить через точки перетину діагоналей протилежних граней. Відрізки між цими точками є паралельними й дорівнюють одному з ребер прямокутного паралелепіпеда.

Прямокутний паралелепіпед має центр симетрії — це точка перетину його діагоналей. Він також має три площини симетрії, які проходять через центр симетрії паралельно граням. Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом.

21. Конус, зрізаний конус

Конус — геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску поверхню; тіло, утворене обертанням прямокутного трик навколо його катета.

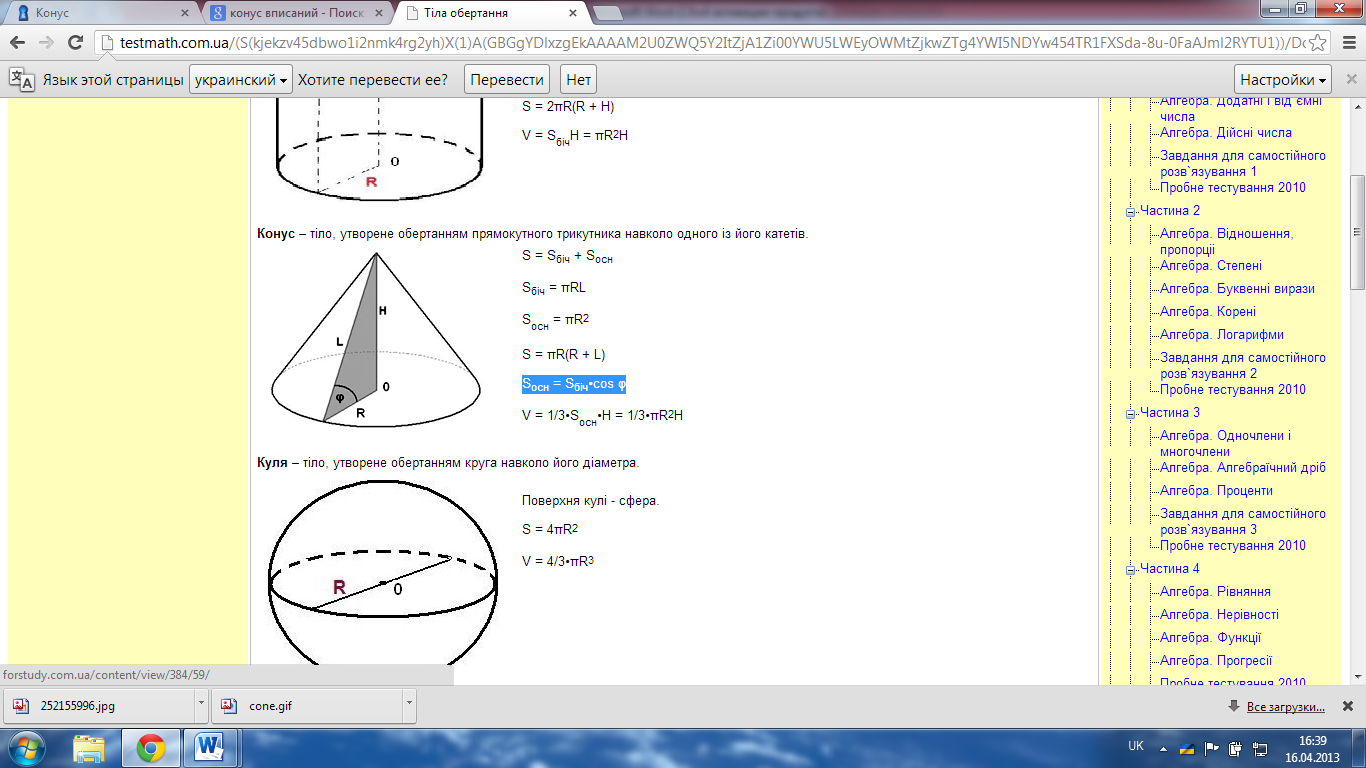
Відрізок, опущений перпендикулярно з вершини на площину основи, називається висотою конуса. Відрізок, який сполуч вершину конуса з будь-якою точкою кола його основи,-твірна конуса.усі твірні конуса рівні. Площина, що прох через твірну конуса і не має з ним інших спільних точок, назив дотич площиною до конуса

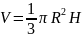; ; ; кут при вершині в осьовому перерізі: ; Об'єм кулі, описаної навколо прямого кругового конуса: ; S_осн = πR^2; S_осн = S_біч•cos φ

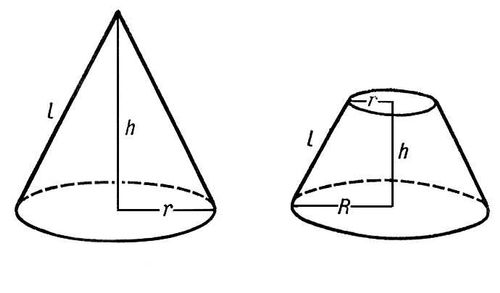
Січна площина,паралельна основі, перетин конус по кругу. При цьому дістанемо два тіла обертання: менший конус, геометричний даному, і зрізаний конус. Зрізаний конус можна розглядати і як тіло, утворене оберт прямокутної трап навколо меншої її бічної сторони

Довжина твірної :

;