10. Многогранники, їх елементи. Види многогранників

Многогранник – це геометричне тіло, поверхня якого складається із скінченого числа плоских многокутників. Гранями многогранника називаються частини площин (многокутники), які обмежують многогранник. Ребрами многогранника називаються спільні сторони суміжних граней (многокутників). Вершинами многогранника називаються вершини многогранних кутів, утворених його гранями, що сходяться в одній точці.

Діагоналлю многогранника називається відрізок прямої, яка сполучає дві вершини многогранника, що не лежать в одній грані. Перерізом многогранника площиною називається частина цієї площини, яка обмежена лінією перетину поверхні многогранника з цією площиною.

Многогранник називається опуклим, якщо він цілком лежить по одну сторону від площини будь-якої його грані. Гранями опуклого многогранника можуть бути тільки опуклі многокутники.

Призма

Висота – відрізок, що міститься між її основами і перпендикулярний до них. Пряма призма – бічні ребра перпендикулярні до основ. Площа б п довільної призми Площа б. п. прямої призми = добутку периметра основи на висоту призми: Об'єм довільної призми

Паралелепіпед – призма, основи якої – паралелограми. У паралелепіпеді протилежні грані паралельні і рівні; всі чотири діагоналі перетинаються в одній точці і діляться нею навпіл. Площа бічної поверхні прямокутного Об'єм прямокутного паралелепіпеда Куб – прямокутний паралелепіпед, усі ребра якого рівні.

Правильна піраміда – в основі лежить правильний многокутник і основа висоти збігається з його центром. Апофема – висота бічної грані правильної піраміди.Площа бічної поверхні правильної піраміди дорівнює одній другій добутку периметра основи на апофему:

Об'єм піраміди:

8. Просторова теорема косинусів

У тетраедрі з прямим тригранним кутом при вершині О дані площі S₁, S₂ іS₃трьох граней, що сходяться у цій вершині. Знайти площу грані, протилежної т.О. Проведений аналіз і для обчислення S знайдена формула

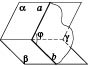
6. Двогранний кут. Бісектор двогранного кута

Означення. Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, тобто ребром двогранного кута. Дві півплощини називаються гранями двогранного кута.

При перетині двох площин утворюється чотири випуклих двогранних кути, у яких лінійні кути менші розгорнутого кута, тобто менші 180^о.

Означення. Два двогранних кути називаються суміжними, якщо вони мають спільну грань, а дві інші грані доповнюють одна одну до площини.

Означення. Бісектором двогранного кута називається множина точок(бісекторна півплощина), що рівновіддалена від граней двогранного кута. Властивості бісекторів:

• Якщо точка О належить ребру двогранного кута, а точка М належить бісекторній півлощині, то пряма ОМ утворює рівні кути з площинами граней даного двогранного кута.

• Бісекторна півплощина розбиває випуклий двогранний кут на два двогранних кути, у яких рівні величини відповідних лінійних кутів.

• Кут між бісекторами двох суміжних двогранних кутів прямий.

• Точка М належить бісектору тоді і тільки тоді, коли ортогональні проекції відрізка ОМ ( точка О – належить ребру двогранного кута) на площини граней мають рівні довжини.

Означення. Два двогранних кути називаються рівними, якщо вони суміщаються при накладанні.

Властивість двогранного кута. Якщо площина перпендикулярна до двох граней двогранного кута, то вона перпендикулярна і до його ребра. І навпаки, якщо площина перпендикулярна до ребра двогранного кута, то вона перпендикулярна і до двох граней двогранного кута.

Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих.