Тема 6. Масштабування у вікні

Перш ніж приступити до обговорення цього питання, зробимо одне невелике зауваження. У вже викладеному матеріалі було описано деякі системами координат: світовими (тема 1, 2, 3), видовими (тема 4, 5), ... . В даній темі ми будемо мати справу з екранними координатами, які, як це вже говорилося, є номери пікселів екрану і використовуються в момент виведення зображення безпосередньо на екран дисплея.

Масштабування.

Для того, щоб виконати масштабування, необхідно:

• задати або визначити координати розміру зображення: x_min, y_min, x_max, y_max і координати області виводу: X_min, Y_min, X_max, Y_max;

• обчислити коефіцієнти масштабування:

• провести обчислення поточних координат екрану:

де x_е, y_е – екранні координати, X_р, Y_р – реальні координати.

Тема 7. Знаходження параметрів площини

Знаходження площині по точкам.

Нехай рівняння ax + by + cz + d = 0 описує площину. Змінна d є вільною, їй можна надати будь-яке значення, покладемо її рівною одиниці: d = 1. Відомо, що площина задається, причому однозначним чином, трьома точками (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) простору (ці точки, взагалі кажучи, не повинні одночасно перебувати на одній прямій ):

Розв’язавши цю систему рівнянь щодо невідомих a, b і c, ми знайдемо рівняння площини.

Покажемо це на прикладі. Знайдемо рівняння площини, що проходить через три точки: A(1, 0, 0), B(0, 1, 0), C(1, -1, 1). Рис. 7.1 ілюструє нашу задачу:

Рис. 7.1.

Уявімо систему рівнянь у вигляді добутку матриць: перша з них містить координати точок A, B і C, друга – невідомі a, b і c, третя – праві частини рівнянь:

Звідси знаходимо a = –1, b = –1, с = –1 і підставляємо їх у рівняння площини:

–1x – 1y – 1z + d = 0,

або x + y + z = d.

Підставимо в це рівняння площини будь-яку точку, наприклад, (1, 0, 0) і знайдемо d: d= 1. Остаточно рівняння даної площини виглядає так: x + y + z – 1 = 0.

Метод визначення площині по нормалі.

Якщо є можливість визначити n – вектор нормалі до площини, – то можна знайти і рівняння цієї площини; n знаходиться як векторний добуток векторів V₁{x₁, y₁, z₁} і V₂{x₂, y₂, z₂}, що лежать в обумовленою площині. В координатній формі це запишеться наступним чином (значок х позначає векторний добуток векторів; i, j, k – одиничні вектори осей х, у і z):

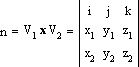
Для простого прикладу, наведеного вище, ми будемо мати наступне:

V₁{0 – 1, 1 – 0, 0 – 0} = V₁{–1, 1, 0},

V₂{1 – 1, –1 – 0, 1 – 0} = V₂{0, –1, 1},

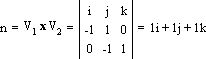
Обчислені коефіцієнти при i, j, k підставляємо в рівняння площини замість a, b і c: 1x + 1y + 1z + d = 0. Взявши довільну точку площини і підставивши її координати замість x, y, z, знайдемо d: C(1, –1, 1), d = –1∙1 –1∙(–1) – 1∙1 = –1. Отже, остаточне рівняння площини прийме наступний вигляд: x + y + z – 1 = 0.

Метод Ньюела.

Цей метод еквівалентний визначенню нормалі в кожній вершині багатокутника допомогою векторного твори прилеглих ребер і усереднення результатів.

Нехай а, b, с, d – коефіцієнти рівняння площині, тоді:

Підсумовування під знаком суми ведеться по i, яке всюди змінюється від 1 до n, де n – це число вершин багатокутника. Змінна j приймає значення 1 при i = n, в іншому випадку j=i+1. Між точками знаходимо середню площину, що проходить через всі точки. У методі відбувається як би обчислення «центру мас».

Спробуємо знайти коефіцієнти для площини, зображеної на рис. 7.1:

a = (y₁ – y₂)∙(z₁ – z₂) + (y₂ – y₃)∙(z₂ – z₃) + (y₃ – y₄)∙(z₃ – z₄) + (y₄ – y₁)∙(z₄ – z₁) =

= (0 – 1)∙(0 + 0) + (1 – 0)∙(0 + 1) + (0 – (–1))∙(1 + 1) + (–1 – 0)∙(1 + 0) = 2 ,

b = ... = 2,

c = ... = 2,

d = – (2x₄ + 2y₄ + 2z₄) = – (2 – 2 + 2) = –2.

Отримуємо площину x + y + z – 1 = 0. Той же самий результат буде, якщо обчислити нормалі кожної з чотирьох вершин і усереднити отримані коефіцієнти.