Тема 1. Перетворення у двомірному просторі

Перетворення в двомірному просторі використовуються в різноманітних випадках: щоб окремі частини об'єкта можна було описувати в різних координатних системах; щоб типові і повторювані частини можна було розташовувати в довільних положеннях на кресленні і в просторі, в тому числі з використанням циклів; щоб без повторного кодування можна було отримувати симетричні частини об'єкта; для спрямованої деформації фігур, тіл і їх частин; для зміни масштабу креслення, побудови проекцій просторових образів, тощо. З аналітичної точки зору перетворення - це перерахунок значень координат.

Перетворення точки.

Точка на площині представляється двома координатами: |x, y|. Матриця перетворення точки виглядає так:

Нижче показано перетворення точки через квадратну матрицю; тут x_n=xa+yc та y_n=xb+yd – нові координати точки після перетворення:

Перетворення фігури.

Якщо уявити фігуру як сукупність точок, то можна провести і її перетворення. У наступному прикладі задано чотири точки: A(0,0), B(1,0), C(1,1), D(0,1), кожна з яких після перетворення переходить відповідно в A*(0,0) , B*(a,b), C*(a+c,b+d), D*(c,d):

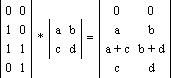
Геометрично це відповідає деформації фігури:

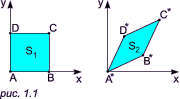
Рис. 1.2.

При цьому площа нової фігури дорівнює площі старої фігури, помноженої на детермінант матриці перетворення: S₂=S₁*|ad-bc|.

Однорідні координати та операції над ними.

Будь-яка система координат, в якій уявлення точки в двомірному (тривимірному) просторі задається за допомогою трьох (чотирьох) координат (Р₁, Р₂, Р₃ (, Р₄)), називається системою однорідних координат. Взагалі, для n-мірного простору число однорідних координат має бути на одиницю більше: n+1.

Застосування однорідних координат в загальному випадку дозволяє усувати аномалії, що виникають при роботі в декартових координатах, і представляти складні перетворення у вигляді добутку декількох матриць.

Геометрична інтерпретація на випадок двомірного простору: введення третьої координати, що дорівнює одиниці, можна трактувати як перехід в тривимірний простір, в якому дозволено працювати тільки в площині z=1. Слід уявляти собі, що екран комп'ютера (картинну площину, площину зображення) знаходиться в площині z=1:

Рис. 1.3.

У разі виходу малюнка за перетин z=1, рисунок повертається примусово у дане січення – для того, щоб були можливі наступні операції:

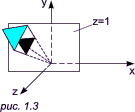
Рис. 1.4.

Така операція називається нормалізацією однорідних координат:

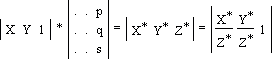
Загальний вигляд перетворення.

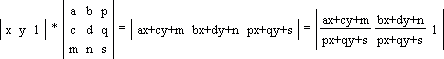
Операція зсуву.

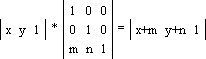
Матриця перетворення містить у собі константи m та n, під дією яких точка зміщується на m одиниць вздовж осі x і на n одиниць – вздовж осі y:

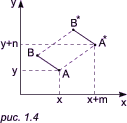
Рис. 1.5.

Операція масштабування.

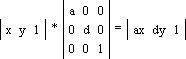
За рахунок коефіцієнтів a і d матриці перетворення відбувається збільшення (або зменшення) значення координат точки (x, y) в a і d раз по осях x та y відповідно:

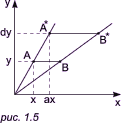
Рис. 1.6.

Загальне повне масштабування.

В даному випадку при s<1 буде відбуватися збільшення значення координат точки (x, y) в s разів; при s> 1 ми отримаємо зворотний ефект – зменшення значення координат (x, y) в s разів.

Поворот на кут :

Тут – кут, на який потрібно повернути точку (x, y).

Зверніть увагу: поворот відбувається відносно точки (0, 0) декартової системи координат проти годинникової стрілки!

Приклад: Спробуємо повернути трикутник на кут , із заданими наступними координатами точок: A(3, -1), B(4, 1), C(2, 1).

Оскільки кут повороту рівний 90 º, відповідно матриця повороту буде мати наступний вигляд:

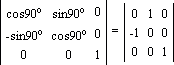
Підставивши значення точок, отримаємо:

Рис. 1.7.

Відповідь: A*(1, 3), B*(-1, 4), C*(-1, 2).

Відображення або віддзеркалювання.

• Віддзеркалення відносно прямої y=x (рис. 1.8a):

• Віддзеркалення відносно прямої x=0 (рис. 1.8b):

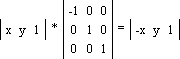
• Віддзеркалення відносно прямої y=0 (рис. 1.8c):

• Віддзеркалення відносно початку координат (рис. 1.8d):

Рис. 1.8.

Поворот фігури навколо довільної точки (m, n) на довільний кут α.

Щоб провести будь-яке складне перетворення, необхідно розкласти його на базові операції. Поворот фігури навколо довільної точки (m, n) на довільний кут a складається з трьох базових операцій: 1) перенесення фігури на вектор A(-m,-n) для суміщення точки (m, n) з початком координат, 2) поворот фігури на кут α, 3) перенос фігури на вектор A'(m, n) для повернення її в початкове положення. Так як фігуру можна уявити набором точок, то операції 1) - 3) можна виконувати послідовно для кожної точки. Покажемо це на прикладі.

Нехай ми хочемо повернути трикутник з координатами A(x, y), B(x₁, y₁), C(x₂, y₂) навколо точки D (m, n) на кут α. Нехай P_-S – матриця переносу точки на вектор A(-m,-n), V_α – матриця повороту на кут α, P_S – матриця переносу точки на вектор A'(m, n).

Отже, ми маємо всі дані, необхідні для проведення складного перетворення першої точки – A(x, y):

Точно такі ж перетворення необхідно провести для решти двох точок трикутника, підставляючи відповідні їх координати замість x і y (послідовність операцій див на рис. 1.9). Таким чином, складна операція розбивається на найпростіші і задається результатом відповідних матриць перетворення, причому порядок, в якому перемножуються матриці, істотно визначає результат.

Рис. 1.9.

Центральне проектування (перспектива).

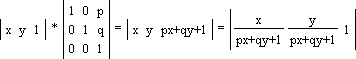
рx + qy + 1 = H – площина.

Примітка:

У загальному випадку від зміни матриць місцями результат змінюється. Матриці операцій, що йдуть підряд, можна перемножувати роздільно, головне – не змінювати їх порядок слідування (див. примітку 1).

Лінії при описаних вище (афінних) перетвореннях переходять в лінії. Тому зазвичай проводиться перерахунок тільки координат вершин фігури, а після цього відповідні вершини в результуючої фігурі з'єднуються, як і у вихідній фігурі.

Афінне перетворення – це відображення , яке можна записати у вигляді .

де М – обернена матриця і .

Інакше кажучи, перетворення називається афінним, якщо його можна отримати наступним чином:

1. Вибрати «новий» базис простору з «новим» початком координат ;

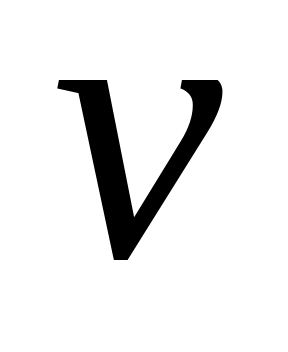2. Кожній точці x простору поставити у відповідність точку f (x), що має ті ж координати щодо «нової» системи координат, що і x в «старій».

Знаходження точки перетину двох ліній (приклад).

Нехай є дві лінії: x + y = 1, 2x – 3y = 0, необхідно знайти точку їх перетину. Рішення може бути знайдено з використанням матриць. Перенесемо всі члени рівнянь в ліву частину: x + y - 1 = 0, 2x – 3y – 0 = 0; запишемо коефіцієнти першого рівняння в перший стовпець матриці, другого рівняння – у другий. Таким чином отримаємо наступну матрицю:

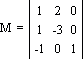
Умова, при якому перетинаються дві прямі, виглядає наступним чином: |x y 1|*M= |0 0 1|.

Для знаходження відповіді необхідно обидві частини попереднього рівняння домножити справа на обернену матрицю M ^-1 (при перемножуванні M і M ^-1 виходить одинична матриця E): |x y 1|*E= |0 0 1|*M ^-1.

|x y 1| = |3/5 2/5 1|

Відповідь: Точка перетину прямих: x = 3/5, y = 2/5.