2. Алгоритмическое конструирование.
Процедура nan.CleanLN.
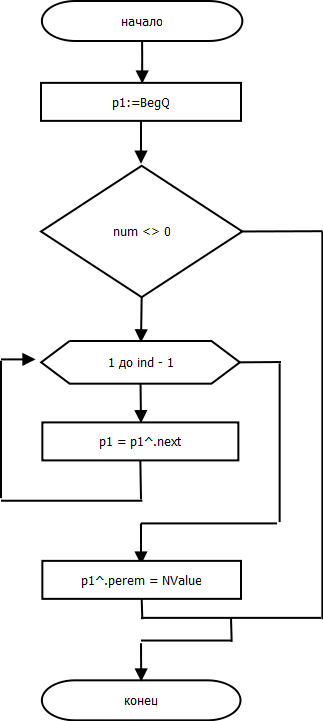
Процедура nan.ChangePerem.
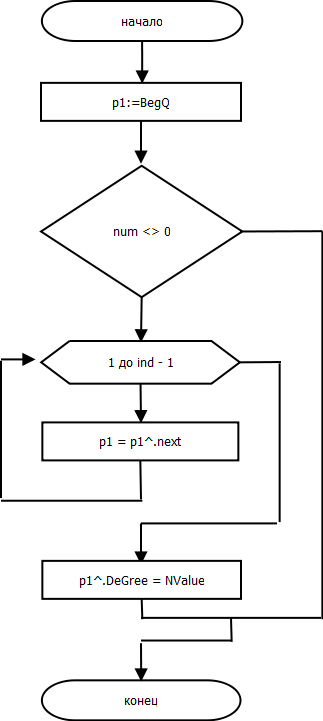
Процедура nan.ChangeDegree.
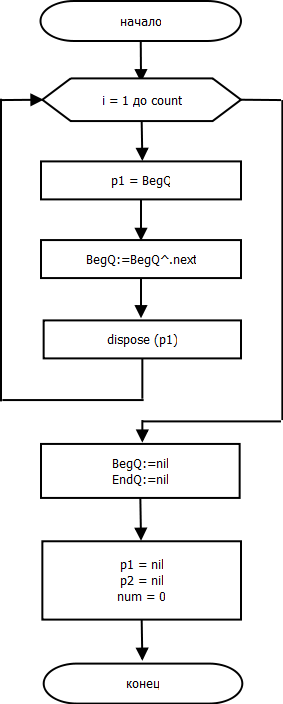
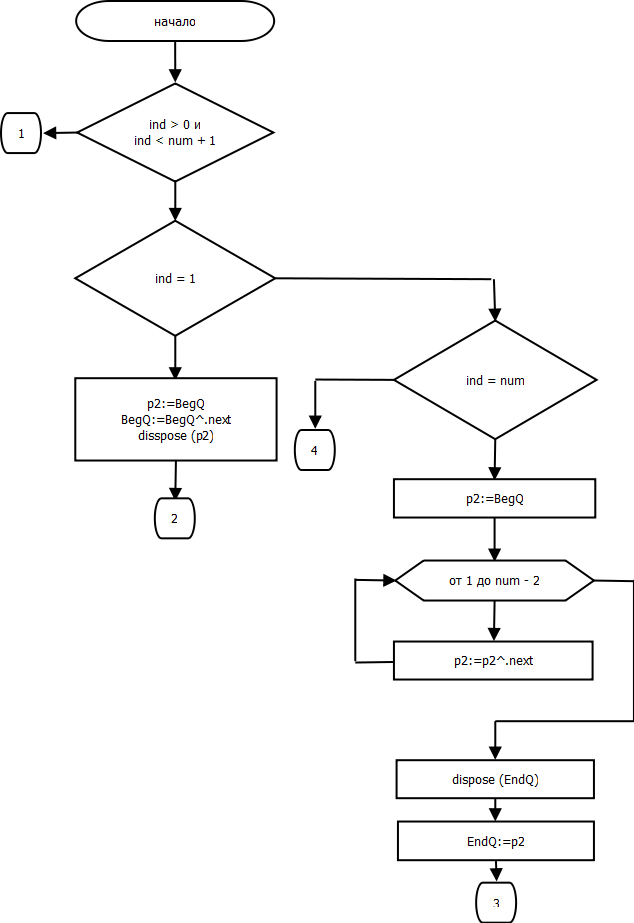
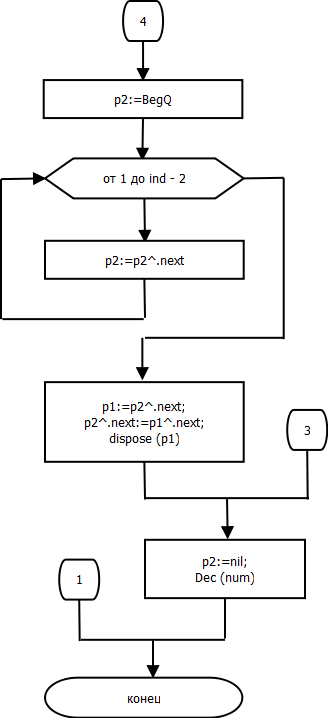
Процедура nan.DisposeN.
Конструктор nan.Create
Процедура nan.Add.
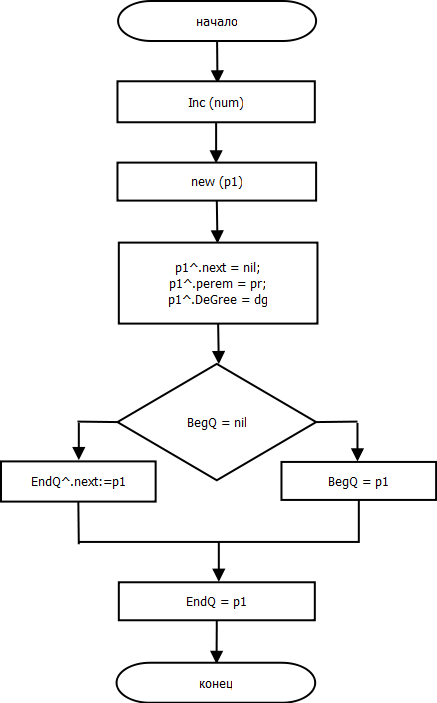
Функция nan.ReturnPerem.
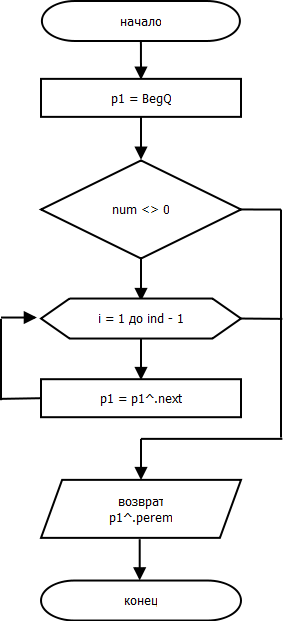
Функция nan.ReturnDegree.
Процедура CreatePolinomial.
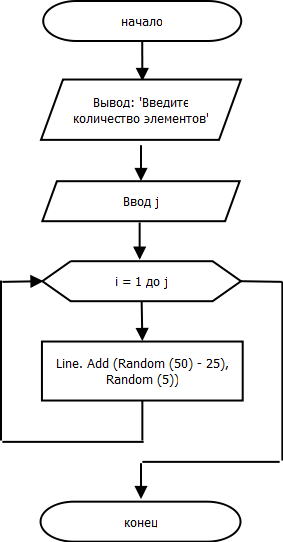
Процедура PrintPolinomial.
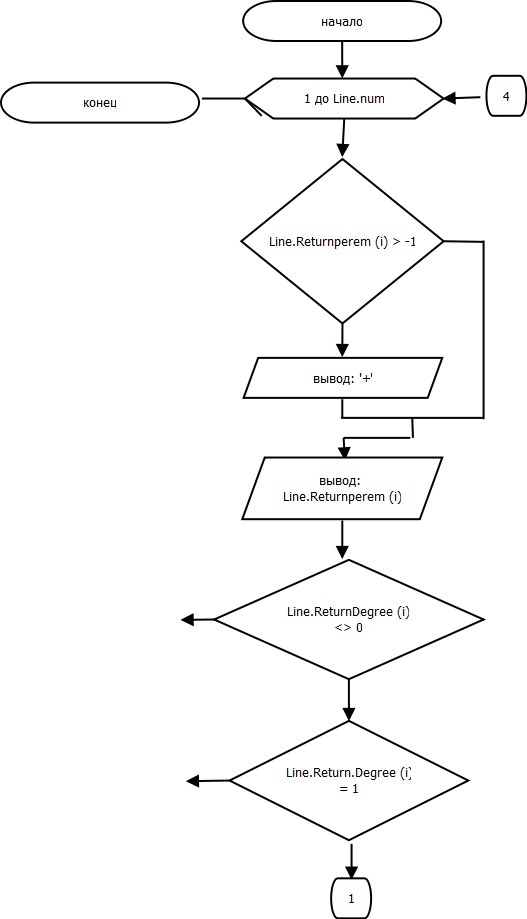
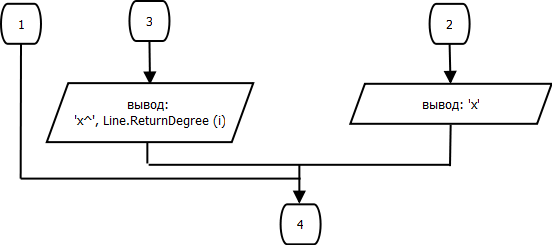
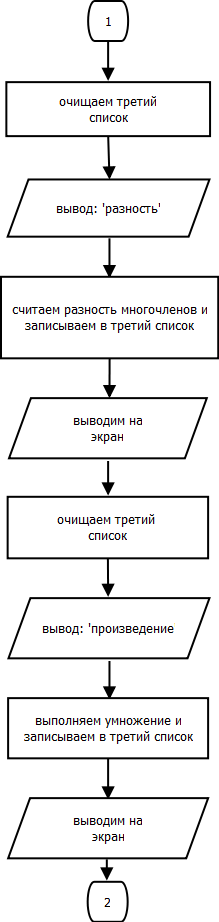
Процедура TotalPolinomial.
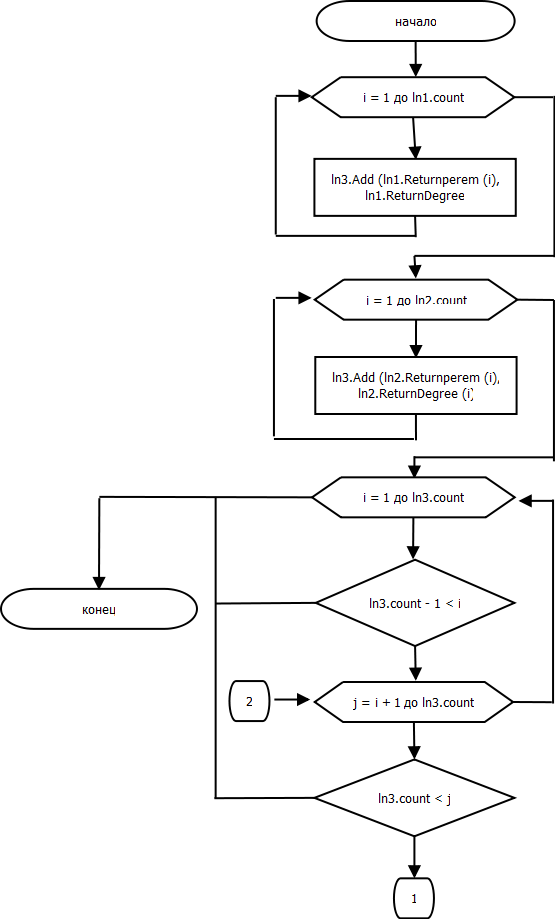
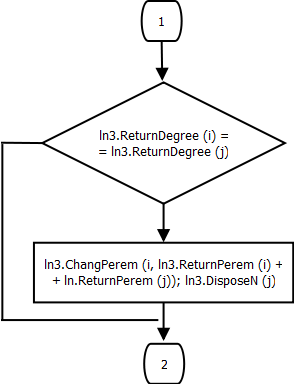
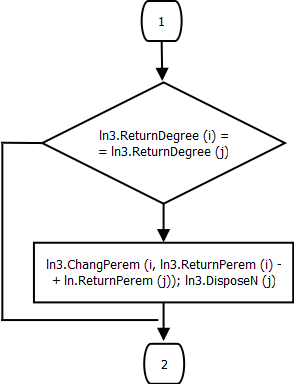
Процедура DifferencePolinomial.
Процедура ProductPolinomial.
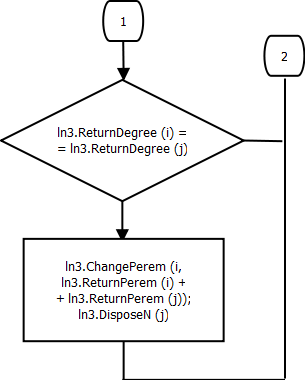
Процедура DerivativePolinomial.
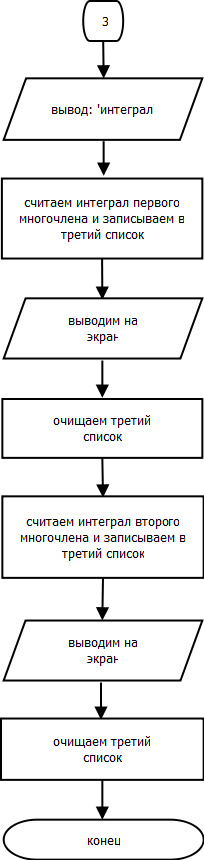
Процедура IntegralPolinomial.
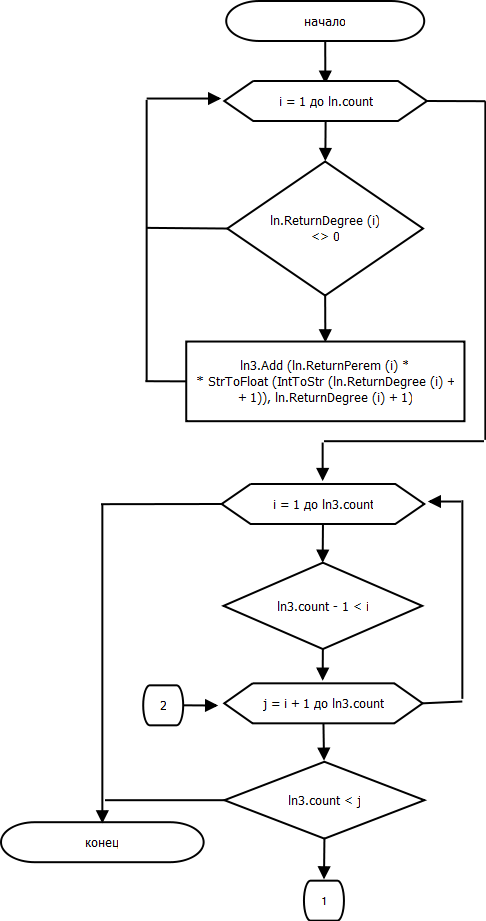
4. Тестирование программы.
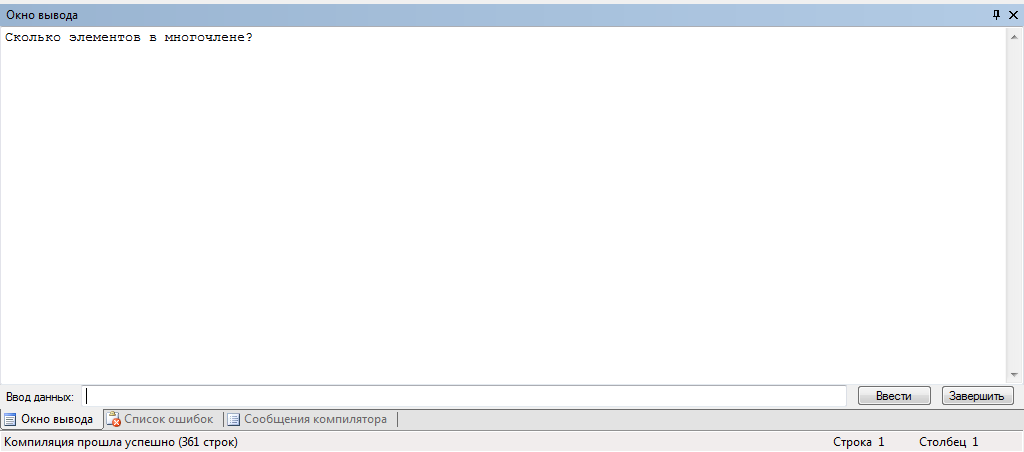
Рис.1
Как мы видим, при запуске программы высвечивается окошко (рис.1).
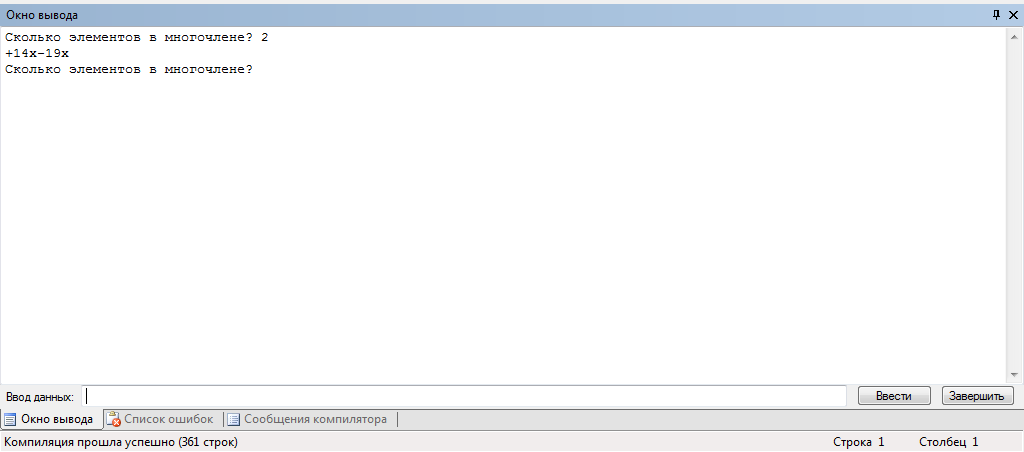
Рис.2
Сначала предлагается ввести количество элементов в первом многочлене, а затем во втором (рис.2).
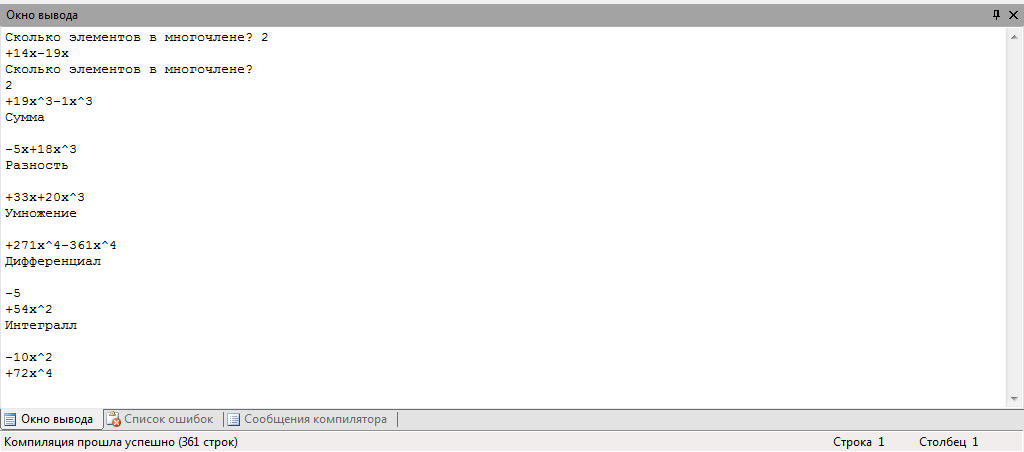
Рис.3
После выполнения этих действий, выводится сумма, разность, произведение, дифференциал и интеграл. Введенных многочленов.
При тестировании программа вела себя стабильно, критических ошибок не возникло. Программа готова к демонстрированию.
Заключение
Разработав данную программу средствами языка PascalABC, я постаралась выполнить требования преподавателя. Моей задачей являлась реализация линей ного списка в компьютерной среде, а именно представление и вычисление многочлена с помощью этой структуры. Надеюсь данная программа включает все требования и будет воспринята преподавателем с лёгкостью.
Список литературы.
1.Т.А. Павловская. «Паскаль. Программирование на языке высокого уровня».
2. Система программирования PascalABC.
Web: http://pascalabc.net.
3. Конспекты А.Н. Румянцева. Лекция «Двоичные деревья».
Приложение.
type
struct = record
perem: real;
Degree: integer;
next: ^struct;
end;
nan = class
protected
BegQ, EndQ, p1, p2: ^struct;
num: byte;
public
constructor Create();
procedure Add(pr: real; dg: integer);
function Returnperem(ind: integer): real;
function ReturnDegree(ind: integer): integer;
procedure ChangePerem(ind: integer; NValue: real);
procedure ChangeDeGree(ind: integer; NValue: integer);
procedure DisposeN(ind: integer);
procedure CleanLN();
property count: byte read num;
end;
procedure nan.CleanLN();
begin
for var i := 1 to count do
begin
p1 := BegQ;
BegQ := BegQ^.next;
dispose(p1);
end;
BegQ := nil;
EndQ := nil;
p1 := nil;
p2 := nil;
num := 0;
end;
procedure nan.ChangePerem(ind: integer; NValue: real);
begin
p1 := BegQ;
if num <> 0 then
begin
for var i := 1 to ind - 1 do
begin
p1 := p1^.next;
end;
p1^.perem := NValue;
end;
end;
procedure nan.ChangeDeGree(ind: integer; NValue: integer);
begin
p1 := BegQ;
if num <> 0 then
begin
for var i := 1 to ind - 1 do
begin
p1 := p1^.next;
end;
p1^.Degree := NValue;
end;
end;
procedure nan.DisposeN(ind: integer);
begin
if (ind > 0) and (ind < num + 1) then
begin
if ind = 1 then
begin
p2 := BegQ;
BegQ := BegQ^.next;
dispose(p2);
end else
if ind = num then
begin
p2 := BegQ;
for var i := 1 to num - 2 do
p2 := p2^.next;
dispose(EndQ);
EndQ := p2;
end else
begin
p2 := BegQ;
for var i := 1 to ind - 2 do
p2 := p2^.next;
p1 := p2^.next;
p2^.next := p1^.next;
dispose(p1);
end;
p2 := nil;
Dec(num);
end;
end;
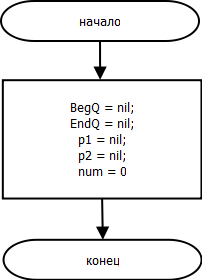
constructor nan.Create();
begin
BegQ := nil;
EndQ := nil;
p1 := nil;
p2 := nil;
num := 0;
end;
procedure nan.Add(pr: real; dg: integer);
begin
Inc(num);
new(p1);
p1^.next := nil;
p1^.perem := pr;
p1^.Degree := dg;
if BegQ = nil then
BegQ := p1
else
EndQ^.next := p1;
EndQ := p1;
end;
function nan.Returnperem(ind: integer): real;
begin
p1 := BegQ;
if num <> 0 then
begin
for var i := 1 to ind - 1 do
begin
p1 := p1^.next;
end;
end;
Result := p1^.perem;
end;
function nan.ReturnDegree(ind: integer): integer;
begin
p1 := BegQ;
if num <> 0 then
begin
for var i := 1 to ind - 1 do
begin
p1 := p1^.next;
end;
end;
Result := p1^.Degree;
end;
procedure CreatePolinomial(var Line: nan);
begin
var j: integer;
write('Сколько элементов в многочлене? ');
readln(j);
for var i := 1 to j do
begin
{ write('Введите множитель: ');
readln(a);
write('Введите степень: ');
readln(b);
Line.Add(a, b);
writeln('Saved! <------!!')}
Line.Add(Random(50) - 25, Random(5))
end;
end;
procedure PrintPolinomial(var Line: nan);
begin
for var i := 1 to Line.num do
begin
if Line.Returnperem(i) > -1 then
write('+');
write(Line.Returnperem(i));
if Line.ReturnDegree(i) <> 0 then
begin
if Line.ReturnDegree(i) = 1 then
write('x')
else
write('x^', Line.ReturnDegree(i));
end;
end;
writeln();
end;
procedure TotalPolinomial(var ln3: nan; ln1, ln2: nan);
begin
for var i := 1 to ln1.count do
ln3.Add(ln1.Returnperem(i), ln1.ReturnDegree(i));
for var i := 1 to ln2.count do
ln3.Add(ln2.Returnperem(i), ln2.ReturnDegree(i));
for var i := 1 to ln3.count - 1 do
begin
if ln3.count-1 < i then break;
for var j := i + 1 to ln3.count do
begin
if ln3.count < j then break;
if ln3.ReturnDegree(i) = ln3.ReturnDegree(j) then
begin
ln3.ChangePerem(i, ln3.Returnperem(i) + ln3.Returnperem(j));
ln3.DisposeN(j);
end;
end;
end;
end;
procedure DifferencePolinomial(var ln3: nan; ln1, ln2: nan);
begin
for var i := 1 to ln1.count do
ln3.Add(ln1.Returnperem(i), ln1.ReturnDegree(i));
for var i := 1 to ln2.count do
ln3.Add(ln2.Returnperem(i), ln2.ReturnDegree(i));
for var i := 1 to ln3.count - 1 do
begin
if ln3.count-1 < i then break;
for var j := i + 1 to ln3.count do
begin
if ln3.count < j then break;
if ln3.ReturnDegree(i) = ln3.ReturnDegree(j) then
begin
ln3.ChangePerem(i, ln3.Returnperem(i) - ln3.Returnperem(j));
ln3.DisposeN(j);
end;
end;
end;
end;
procedure ProductPolinomial(var ln3: nan; ln1, ln2: nan);
begin
for var i := 1 to ln1.count do
begin
for var j := 1 to ln2.count do
ln3.Add(ln1.Returnperem(i) * ln2.Returnperem(j), ln1.ReturnDegree(i) + ln2.ReturnDegree(j));
end;
for var i := 1 to ln3.count - 1 do
begin
if ln3.count < i then break;
for var j := i + 1 to ln3.count do
begin
if ln3.count < j then break;
if ln3.ReturnDegree(i) = ln3.ReturnDegree(j) then
begin
ln3.ChangePerem(i, ln3.Returnperem(i) + ln3.Returnperem(j));
ln3.DisposeN(j);
end;
end;
end;
end;
procedure DerivativePolinomial(var ln3: nan; ln: nan);
begin
for var i := 1 to ln.count do
begin
if ln.ReturnDegree(i) <> 0 then
ln3.Add(ln.Returnperem(i) * StrToFloat(IntToStr(ln.ReturnDegree(i))), ln.ReturnDegree(i) - 1);
end;
for var i := 1 to ln3.count - 1 do
begin
if ln3.count < i then break;
for var j := i + 1 to ln3.count do
begin
if ln3.count < j then break;
if ln3.ReturnDegree(i) = ln3.ReturnDegree(j) then
begin
ln3.ChangePerem(i, ln3.Returnperem(i) + ln3.Returnperem(j));
ln3.DisposeN(j);
end;
end;
end;
end;
procedure IntegralPolinomial(var ln3: nan; ln: nan);
begin
for var i := 1 to ln.count do
begin
if ln.ReturnDegree(i) <> 0 then
ln3.Add(ln.Returnperem(i) * StrToFloat(IntToStr(ln.ReturnDegree(i) + 1)), ln.ReturnDegree(i) + 1);
end;
for var i := 1 to ln3.count - 1 do
begin
if ln3.count < i then break;
for var j := i + 1 to ln3.count do
begin
if ln3.count < j then break;
if ln3.ReturnDegree(i) = ln3.ReturnDegree(j) then
begin
ln3.ChangePerem(i, ln3.Returnperem(i) + ln3.Returnperem(j));
ln3.DisposeN(j);
end;
end;
end;
end;
procedure help(messege: string[255]);
begin
if Length(messege) > 0 then
writeln(messege);
writeln('**********************************************************');
writeln('** 1 - Ввести первый многочлен **');
writeln('** 2 - Ввести второй многочлен **');
writeln('** 3 - Посчитать и вывести сумму многочленов **');
writeln('** 4 - Посчитать и вывести разность многочленов **');
writeln('** 5 - Посчитать и вывести произведение многочленов **');
writeln('** 6 - Посчитать и вывести производную многочлена **');
writeln('** 7 - Посчитать и вывести интеграл многочлена **');
writeln('**********************************************************');
end;
var
line1, line2, line3: nan;
begin
line1 := new nan();
line2 := new nan();
CreatePolinomial(line1);
PrintPolinomial(line1);
CreatePolinomial(line2);
PrintPolinomial(line2);
line3 := new nan();
write('Сумма');
TotalPolinomial(line3, line1, line2);
writeln(); writeln();
PrintPolinomial(line3);
line3.CleanLN();
write('Разность');
DifferencePolinomial(line3, line1, line2);
writeln(); writeln();
PrintPolinomial(line3);
line3.CleanLN();
write('Умножение');
ProductPolinomial(line3, line1, line2);
writeln(); writeln();
PrintPolinomial(line3);
line3.CleanLN();
write('Дифференциал');
DerivativePolinomial(line3, line1);
writeln(); writeln();
PrintPolinomial(line3);
line3.CleanLN();
DerivativePolinomial(line3, line2);
PrintPolinomial(line3);
line3.CleanLN();
write('Интегралл');
IntegralPolinomial(line3, line1);
writeln(); writeln();
PrintPolinomial(line3);
line3.CleanLN();
IntegralPolinomial(line3, line2);
PrintPolinomial(line3);
line3.CleanLN();
end.