
- •Информационные базы данных и сети
- •Часть 1 – «Базы данных и системы управления базами данных»;
- •Часть2 – «Информационно-вычислительные сети» Базы данных и системы управления базами данных
- •Файлы и файловые системы
- •Введение в базы данных и субд Определения баз данных и систем управления базами данных
- •Функции, структура и основные характеристики субд
- •Типы моделей данных
- •Теоретические основы реляционной модели данных
- •Базовые понятия теории множеств
- •Структура реляционной модели данных
- •Целостность реляционных данных
- •Элементы реляционной алгебры
- •Введение в язык sql
- •Разработка баз данных Этапы разработки баз данных
- •Логическая модель данных. Понятие нормализации отношений
- •Oltp и olap системы
- •Основные сведения об информационно-вычислительных сетях
- •1 Основные понятия архитектуры открытых систем
- •1.1 Эталонная модель взаимосвязи открытых систем
- •1.2 Функции уровней Прикладной уровень a
- •Представительный уровень p
- •Сеансовый уровень s
- •Транспортный уровень t
- •Сетевой уровень n
- •Канальный уровень dl
- •Физический уровень pl
- •1.3 Представление сервиса в модели вос
- •4 Правила описания сервиса
- •Аналитические модели смо, используемые для анализа сетей эвм Обозначения, принятые в теории массового обслуживания
- •Общие соотношения
- •Открытые марковские сети
- •Задача Клейнрока
- •Задача выбора пропускных способностей
- •Случай альтернативной (адаптивной) маршрутизации
- •Анализ сквозной задержки пары отправитель-получатель
- •Анализ систем с множественным доступом Коммутация пакетов при передаче через спутник
- •Чистая aloha
- •Синхронная aloha
- •Модель с конечным числом пользователей
- •Коммутация пакетов при наземной радиосвязи
- •Ненастойчивый мдпн
Задача выбора пропускных способностей
Оптимальный (с точки зрания соотношения времени задержки и стоимости) выбор пропускных способностей из конечного набора их возможных значений.
Решается задача
определения
для сети с заданной топологией и
известными потоками
![]() .
Необходимо, чтобы выполнялось ограничение
.
Необходимо, чтобы выполнялось ограничение
![]()
Рассматривается
линейная функция стоимости:
![]() ,
где
,
где
![]() - стоимость в расчете на единицу пропускной
способности i-го
канала.
часто берется пропорциональным физической
длине канала.
- стоимость в расчете на единицу пропускной
способности i-го
канала.
часто берется пропорциональным физической
длине канала.
Задача
![]()
Составим функцию Лагранжа: (метод неопределенных множителей Лагранжа)

Составим систему M уравнений:

Найдем постоянную :
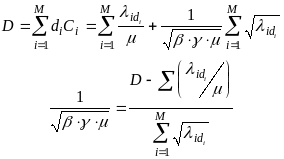
Определим добавочную стоимость как
![]()
Тогда
 (набор пропускных способностей по закону
(набор пропускных способностей по закону
![]() )
)
каждый канал имеет
пропускную способность по крайней мере
![]() и кроме того некоторую дополнительную
пропускную способность. При этом
минимальная средняя задержка в сети
и кроме того некоторую дополнительную
пропускную способность. При этом
минимальная средняя задержка в сети
![]() ,
пропускные способности каналов в которой
выбраны оптимально:
,
пропускные способности каналов в которой
выбраны оптимально:
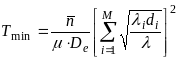
при
![]() средняя задержка пакета в сети
неограниченно возрастает. Если
средняя задержка пакета в сети
неограниченно возрастает. Если
![]() ,
задача ВПС имеет реализуемое решение
(т. е.
,
задача ВПС имеет реализуемое решение
(т. е.
![]() ).
Это условие является условием устойчивости.
).
Это условие является условием устойчивости.
Если
![]() ,
задача не имеет реализуемого решения.
,
задача не имеет реализуемого решения.
При
![]() -
спутниковые каналы
-
спутниковые каналы ![]()

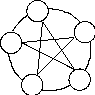
![]() топологическую
структуру сети следует выбирать так,
чтобы получить минимальную среднюю
задержку - полносвязная сеть.
топологическую
структуру сети следует выбирать так,
чтобы получить минимальную среднюю
задержку - полносвязная сеть.
![]() в числителе
минимизируется, когда одна из величин
равна 1, остальные 0 - весь трафик направлен
по одному каналу - вырожденный случай.
Однако можно сделать вывод, что большую
часть трафика нужно посылать по нескольким
скоростным каналам и лишь малую часть
по остальным каналам.
в числителе
минимизируется, когда одна из величин
равна 1, остальные 0 - весь трафик направлен
по одному каналу - вырожденный случай.
Однако можно сделать вывод, что большую
часть трафика нужно посылать по нескольким
скоростным каналам и лишь малую часть
по остальным каналам.
Обычно для связи требуются по крайней мере один входящий и один исходящий каналы для каждого узла. Такая сеть представляет собой кольцо. Но в этой сети средняя длина пути пропорциональна числу каналов M и зависит от распределения входящей нагрузки .
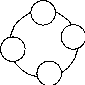
Другая сеть, в
которой также имеется один входящий и
один исходящий канал на каждый узел, за
исключением центрального,- звездообразная.
В этом случае достигается относительно
высокая концентрация трафика на каждой
линии и средняя длина пути
![]() .
.
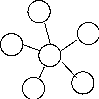
Теперь следует
сделать выбор между полносвязной сетью,
звездообразной сетью и всеми сетями,
промежуточной между ними. Клейнрок
показал, что при
![]() наиболее подходящей является звездообразная
сеть, а при
наиболее подходящей является звездообразная
сеть, а при
![]() - полносвязная сеть. Можно ожидать, что
между этими двумя экстремумами приемлемую
топологию дает добавление некоторых
прямых каналов к звездообразной сети.
- полносвязная сеть. Можно ожидать, что
между этими двумя экстремумами приемлемую
топологию дает добавление некоторых
прямых каналов к звездообразной сети.
Полученные выше выводы относятся к фиксированным процедурам выбора маршрутов.
Случай альтернативной (адаптивной) маршрутизации
Адаптивная маршрутизация предлагает более чем один путь для трафика, направляемого к данному месту назначения, и дает упорядочение по предпочтению этих путей - более длинные пути менее предпочтительны, нежели прямой путь. (Обычно оценивается число переприемов - длина пути, состояние каналов - нет очереди к исходящим каналам). Поэтому допускающие альтернативы процедуры выбора маршрутов приводят к увеличению длины пути для пакетов, и в то же время они стремятся распределить трафик по многим каналам, а не концентрировать его лишь на нескольких каналах. Поэтому при процедуре маршрутизации, допускающей альтернативы, нарушаются условия задачи Клейнрока и решение будет неоптимальным. Т. е. фиксированные маршруты оказываются лучше маршрутов, допускающих альтернативы (с точки зрения задержкастоимость). Это относится к предположению, что величины известны и постоянны.
Если они неизвестны, либо меняются во времени, либо и то, и другое, то нельзя найти и оптимально распределить трафик .
Т. о. в некоторые периоды времени сеть не будет оптимальной. Если рассогласование велико, то необходимо введение адаптивной (допускающей альтернативы) процедуры выбора маршрутов.
Резюме
Если входные параметры (а именно ) известны, то в предположении линейной функции стоимости можно проектировать оптимальные сети в смысле выбора пропускных способностей, которые в точности соответствуют направляемому фиксированной процедурой выбора маршрутов трафику сети.
Если неизвестны или меняются во времени, можно использовать допускающую альтернативы процедуру выбора маршрутов, которая позволяет трафику приспособиться к неудачному набору пропускных способностей.
Приодическое
обновление таблицы маршрутизации
выбор наиболее предпочтительного маршрута для данной пары отправитель-получатель
