Общие соотношения

1. Коэффициент загрузки (коэфф. использования) - математическое описание доли используемой пропускной способности системы

- стабильные системы

2. Связь между временем нахождения заявки в системе и временем ее пребывания в очереди

, W - цена, которую платит клиент за совместное использование

системных ресурсов с другими клиентами

3. Формула Литтла связь числа требований в системе с интенсивностью нагрузки

Для системы G/G/m

Для системы M/M/1 - система с пуассоновским входящим потоком и экспоненциальным обслуживанием - описывается частным случаем марковского процесса с непрерывным временем - процессом разложения/гибели; состояние системы за любой бесконечно малый прмежуток времени изменяется не более чем на единицу

- пуассоновское распределение - вероятность того, что за время t поступит ровно k требований

- вероятность наличия k требований в системе

Для системы M/M/m - система с бесконечной очередью

- стационарная вер-ть застать k требований в системе

- вероятность того, что система пуста

,

где - вероятность того, что система содержит m и более заявок

Вероятность того, что поступившее требование будет ждать обслуживания:

- C-формула Эрланга

- C-формула Эрланга

Система с потерями, в которой в любой момент времени может находиться не более m требований

В-формула Эрланга

Открытые марковские сети

Открытые - в смысле поступления требований извне и ухода их из сети

N узлов, в каждом приборов (показательного обслуживания)

Структура i-го узла

секунд - среднее время

- внешний пуассоновский источник с интенсивностью требований/с

- вероятность поступления требования из узла i в узел j

- вероятность покидания сети

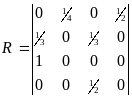
- матрица

интенсивность поступления требований в i-й узел

В сетях с петлями процессы поступления требований в разные узлы не являются пуассоновскими. Однако удивительный факт, известный как теорема Джексона, утверждает, что каждый узел ведет себя так, как если бы его вход был пуассоновским. Если - стационарная вероятность того, что в i-м узле находится требований (i=1,2,...N), то при для всех i согласно этой теореме

(теорема декомпозиции для открытых марковских сетей - теорема Джексона)

- стационарная вероятность того, что требований находятся в системе при интенсивности входящего потока и среднем времени обслуживания

Задача Клейнрока

Сеть с коммутацией сообщений (пакетов) имеет N узлов и M каналов. Каналы бесшумные и абсолютно надежные, пропускная способность i-го канала бит/с. Все i узлов соответствуют узлам коммутации сообщений (пакетов), абсолютно надежны, выполняют сборку/разборку сообщений, выбор маршрутов, хранение в буферах (протоколы 1,2,3 уровней). Модель учитывает очереди к каналам и время передачи пакета по каналам. Время обработки пакета в узле пока не учитывается.

Трафик поступающих в сеть пакетов от внешних источников образует пуассоновский процесс со средним - пакет, приходящий в узел i и предназначенный для узла k.

Полный внешний трафик, поступающий в сеть и покидающий ее определим как

Длины всех пакетов независимы и распределены по показательному закону со средним значением бит. Для размещения этих пакетов в узлах сети имеется память неограниченной емкости. Используется процедура фиксированного выбора маршрутов. Это означает, что для данной пары источник-адресат в сети имеется только один путь.

Поскольку каждый канал в сети рассматривается как отдельный обслуживающий прибор, обозначим через среднее число пакетов в секунду, проходящих по i-му каналу. Полный трафик в сети:

Стоимость построения (капитальные затраты) i-го канала с пропускной способностью задается функцией стоимости , зависящей от номера и пропускной способности канала. Стоимость всей сети (стоимость узлов включается в стоимость каналов связи)

Определим задержку в сети как полное время, которое пакет проводит в сети. Будем говорить о средней задержке пакета в сети T.

Обозначим через путь, по которому идут пакеты, возникающие в узле j и имеющие в качестве узла назначения узел k. i-ый канал с пропускной способностью включен в путь , если пакеты, идущие по этому пути, проходят этот канал. Поэтому:

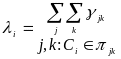
Обозначим - среднее время задержки пакета в канале i, включая среднее время ожидания в очереди к i-му каналу и среднее время передачи пакета со средней длиной бит по каналу со скоростью бит/с -

Для системы M/M/1, описывающей канал

Применяя формулу Литтла для всей сети, имеем: среднее число пакетов в сети равно . Среднее число пакетов, ожидающих или использующих i-ый канал, равно Тогда

- вогнутая функция

если сеть не нагружена, т. е. и

к определенному пределу.

Введем понятие длины пути :

= длина пути - число каналов, входящих в путь .

Средняя длина пути

(1) - инвариантна по отношению к уровню трафика

(2)

тогда, подставляя (2) в (1), получим:

и

- остается постоянным (не зависит от нагрузки на сеть ) и является функцией лишь процедуры выбора маршрутов.