
- •Глава 6. Определенный интеграл
- •6.1. Понятие определенного интеграла
- •6.2. Свойства определенного интеграла
- •6.3. Формула Ньютона-Лейбница
- •6.4. Замена переменной в определенном интеграле
- •6.5. Интегрирование по частям в определенном интеграле
- •6.6. Геометрические приложения определенного интеграла
- •6.7. Несобственные интегралы
- •6.8. Применение определенного интеграла в экономике
- •Примеры решения задач к главе 6
- •Задания для самостоятельного решения
Задания для самостоятельного решения
Вычислить определенные интегралы:
6.1.
![]() 6.2.
6.2.
![]()
6.3.
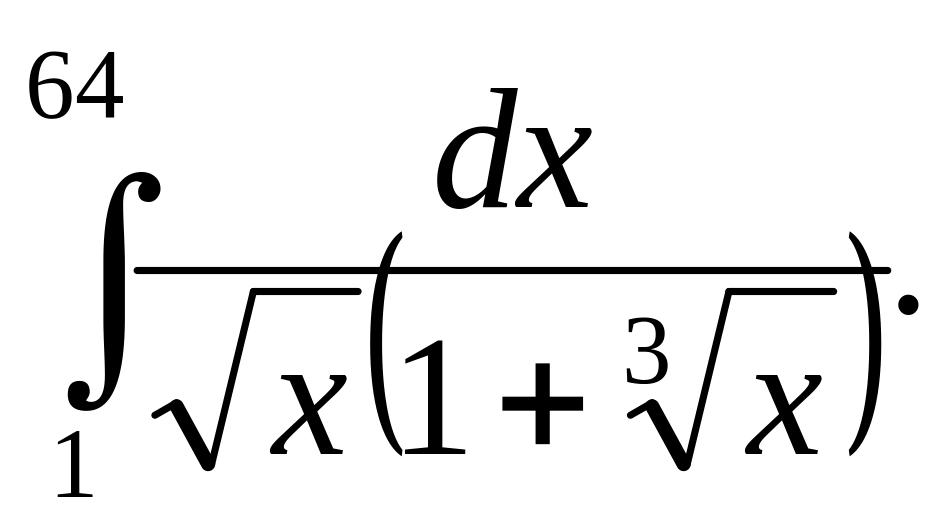 6.4.
6.4.
![]()
6.5.
![]() 6.6.
6.6.
![]()
6.7.
![]() 6.8.
6.8.
![]()
6.9.
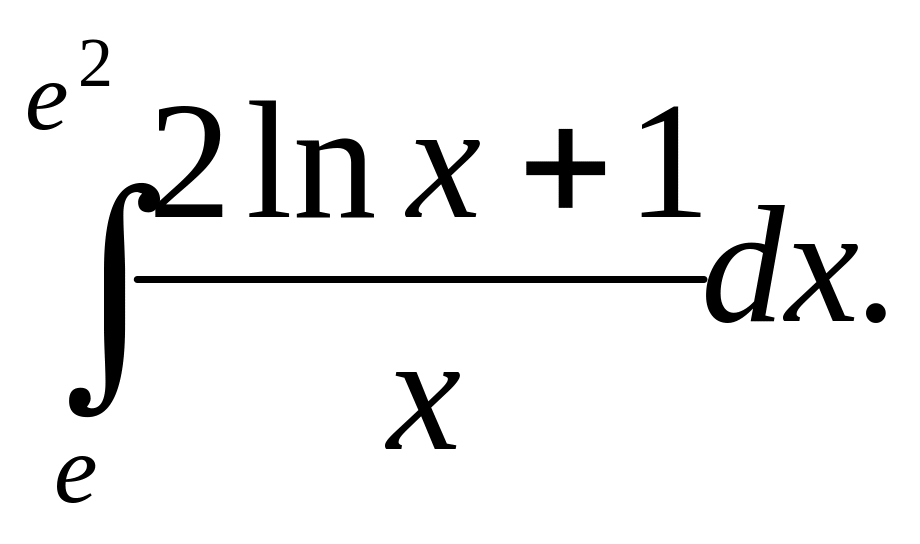 6.10.
6.10.
![]()
6.11.
![]() 6.12.
6.12.
![]()
6.13.
![]() 6.14.
6.14.
![]()
6.15.
![]() 6.16.
6.16.
![]()
6.17.
![]() 6.18.
6.18.
![]()
6.19.
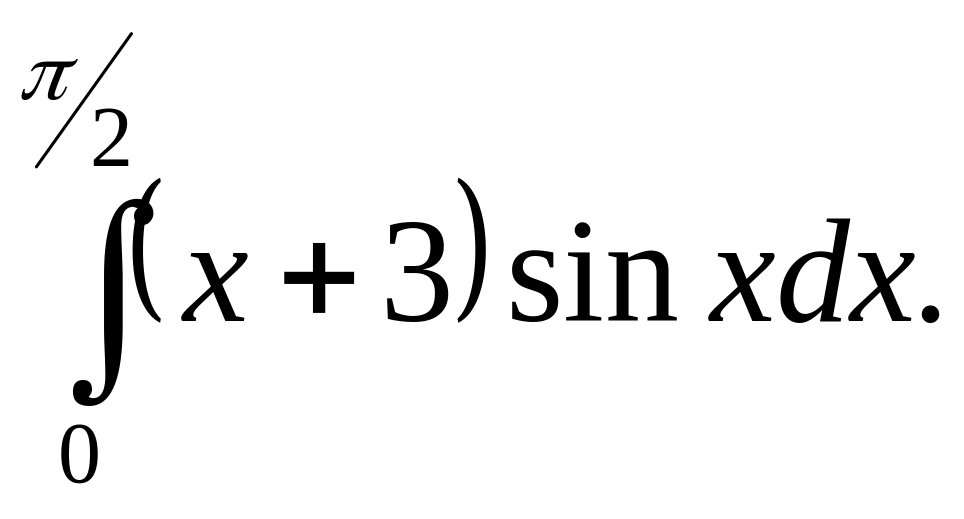 6.20.
6.20.
![]()
6.21.
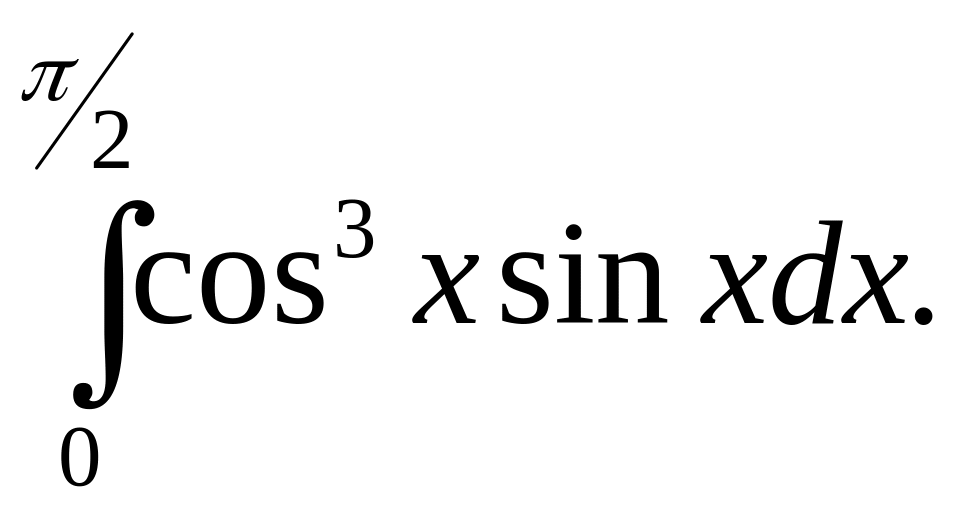 6.22.
6.22.
![]()
6.23.
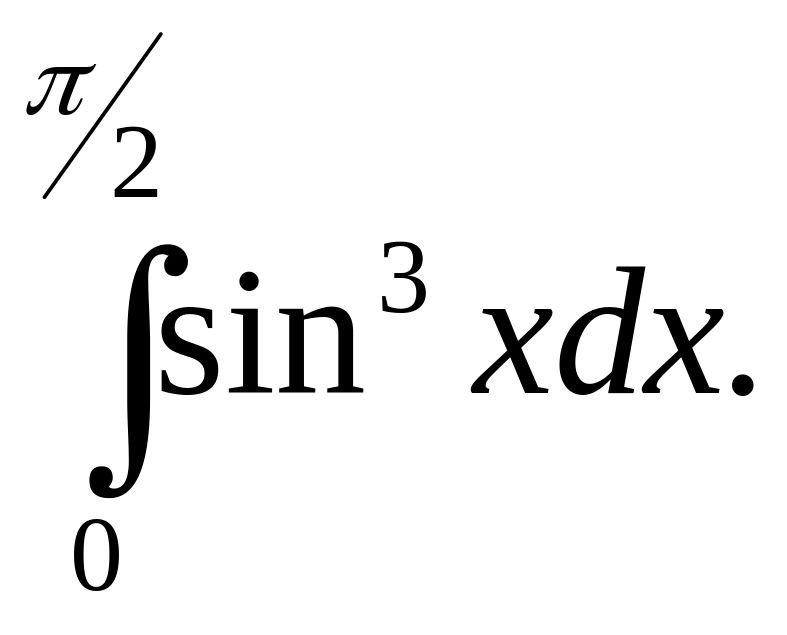 6.24.
6.24.
![]()
6.25.
![]() 6.26.
6.26.
![]()
6.27.
![]() 6.28.
6.28.
![]()
6.29.
![]() 6.30.
6.30.
![]()
6.31.
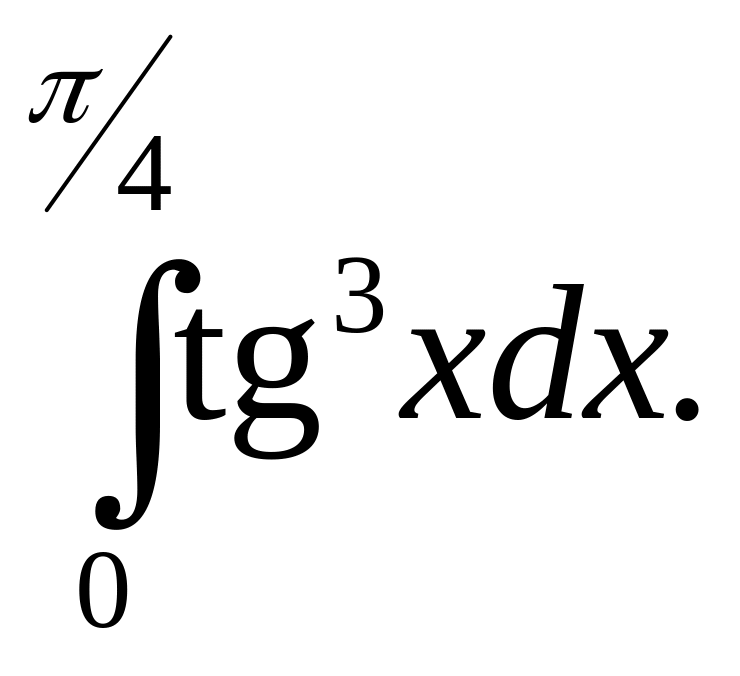 6.32.
6.32.
![]()
Вычислить несобственные интегралы (если они сходятся):
6.33.
![]() 6.34.
6.34.
![]()
6.35.
![]() 6.36.
6.36.
![]()
6.37.
![]() 6.38.
6.38.
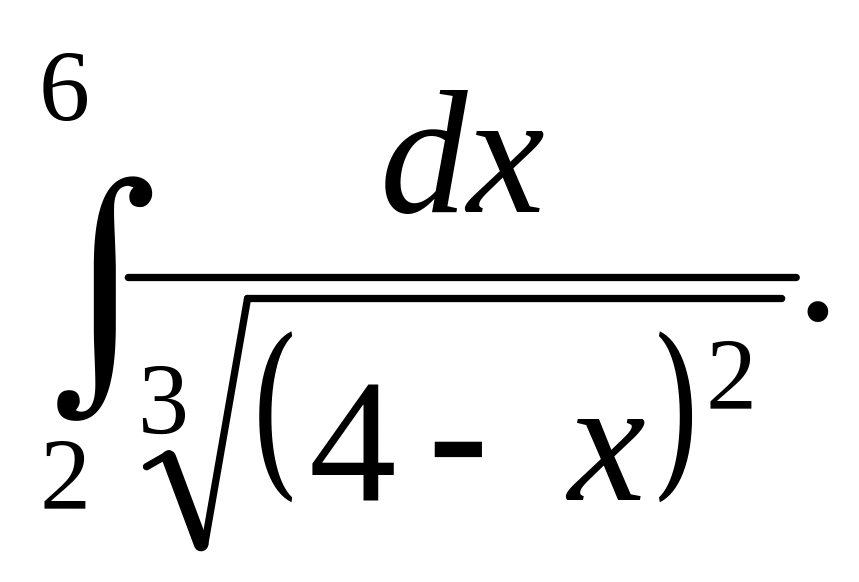
6.39.
![]() 6.40.
6.40.
![]()
6.41.
![]() 6.42.
6.42.
![]()
6.43.
![]() 6.44.
6.44.
![]()
6.45.
![]() 6.46.
6.46.
![]()
6.47.
![]() 6.48.
6.48.
![]()
6.49.
![]() 6.50.
6.50.
![]()
6.51.
![]() 6.52.
6.52.
![]()
6.53.
![]() 6.54.
6.54.
![]()
6.55.
![]() 6.56.
6.56.
![]()
6.57.
![]() 6.58.
6.58.
![]()
Вычислить площади фигур, ограниченных заданными линиями:
6.59. у = – х2, х + у + 2 = 0.
6.60. у = 16/x2, у =17 – х2 (I четверть).
6.61. у2 = 4х3, y = 2x2.
6.62. xy = 20, х2 + y2 = 41 (I четверть).
6.63. y = sinx, y = cosx, x = 0.
6.64. у
= ех,
у =![]() ,
у = е2.
,
у = е2.
6.65. у = х4 – 2х2, у = 0.
6.66. у = 3 + 2х – х2, у = х + 1.
6.67. у = х2 + 3, ху = 4, у = 2, х = 0.
6.68. у = х2, у = -2х2 + 3х (фигура расположена в первой четверти).
6.69. у
=![]() ,
у = х +
1.
,
у = х +
1.
6.70. у
= cos2x,
y
= 0,
x
= 0,
x
=
![]() .
.
6.71. у = 2 – х4, у = х2.
6.72. ху = 1, у = х2, х = 3, у = 0.
6.73. y
=
![]() ,
y
= 2 –
x,
y
= 0.
,
y
= 2 –
x,
y
= 0.
6.74. у
=
![]() ,
у
= х,
х
= 2.
,
у
= х,
х
= 2.
6.75. у = х2 – 2х + 3, у = 3х – 1.
6.76. у
= х2,
у = 1
+![]() х2.
х2.
6.77. у
=
![]() ,
у =
,
у =
![]()
6.78. у = х2 + 2, у = 1 – х2, х = 0, х = 1.
6.79. у = – х2, у = 2ех, х = 0, х = 1.
6.80. у
=
![]() ,
x
= 1,
y
= x
– 1.
,
x
= 1,
y
= x
– 1.
6.81. y
=
,
y
=
![]() ,
y
= 0.
,
y
= 0.
6.82. у = lnх, х = е, у = 0.
6.83. х = 0, х = 2, у = 2х, у = 2х – х2.
6.84.
у =
arcsin2x,
х =
0, у =
![]() .
.
6.85. у = х2 + 1, х = у 2, 3х + 2у – 16 = 0, x = 0.
6.86. у = (х + 1)2, у 2 = х + 1.
6.87. у = 4 – х, у = х2 – 2х, у = 0 (фигура расположена во второй четверти).
6.88. y
=
![]() х2 +
2,
x
+ 2y
– 4 = 0, y
= 0.
х2 +
2,
x
+ 2y
– 4 = 0, y
= 0.
Вычислить длины дуг кривых:
6.89. y= lnsin х от x = π/3 до х = π/2.
6.90. y
= (2/5)х![]() (2/3)
(2/3)![]() между точками
пересечения
между точками
пересечения
с осью Oх.
6.91. y = х2/2 от х = 0 до x=l.
6.92. у=1 – lncosx от x = 0 до x = π/6.
6.93 x = etcos t, y = etsint от t = 0 до t = lnπ.
6.94. x = 8sint + 6cost, y = 6sint — 8cost от t = 0 до t = π/2.
Найти объемы тел, образованных при вращении вокруг осей Ох и Оу плоских фигур, ограниченных линиями:
6.95. у = х3, у = 4х.
6.96. y = sinx, у = 0, при 0 ≤ x ≤ π.
6.97.
у =
![]() ,
х
= 1, х = 4,
у = 0.
,
х
= 1, х = 4,
у = 0.
6.98.
у =
![]() –
2х,
у = 0.
–
2х,
у = 0.
6.99. у = х2, ху = 8, у = 0, х = 4.
6.100.
х =
![]() ,
х = 0,
у = 5.
,
х = 0,
у = 5.
6.101. у = lnх, у = 0, х = е.
6.102. у = –x2 + 4, у = х2, х = 0.
6.103. у
=
![]() ,
у
=
,
у
=
![]() ,
х
= 0.
,
х
= 0.
6.104. у = x2 + l, х = у 2 + 1, у = 0, у = 0, х = 2.
6.105. у = 4 – х2, у = 0, х = 0, где х ≥ 0.
6.106. у = ех, х = 0, х = 1, у = 0.
6.107. y = x2 + 1, y = 0, х = 1, х = 2.
6.108. у = х3, у = 1, х = 0.
6.109. Производительность труда рабочего в течение дня задается функцией z(t) = –0,00625t2 + 0,05t + 0,5 (ден. ед/ч), где t – время в часах от начала работы (0 ≤ t ≤ 8). Найти функцию и = u(t), выражающую объем продукции от времени t (в денежных единицах) и его величину за рабочий день.
6.110. Определить объем выпуска продукции за первые 5 ч работы при производительности f(t) = 11,3e -0,417t, где t – время в часах.
6.111. Найти объем продукции, выпущенной предприятием за год (258 рабочих дней), если ежедневная производительность этого предприятия задана функцией f(t)= –0,0033t2 – 0,089t + 20,96, где t – время в часах (1 ≤ t ≤ 8).
6.112. Найти объем выпуска продукции за четыре года, если в функции Кобба–Дугласа A(t) = e3t, L(t) = t + 1, K(t) = 10, а0 = α = β = γ = 1.
