6.7. Несобственные интегралы

Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций.

Несобственный интеграл от функции в пределах от до определяется равенством

.

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности, – расходящимся.

Аналогично,

.

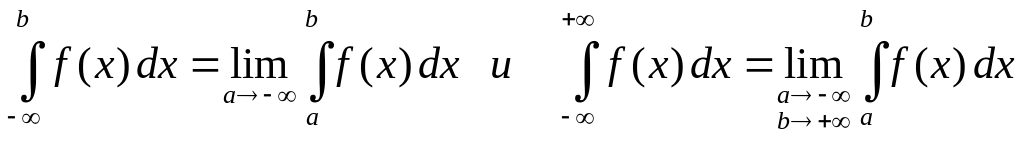Если функция f (х) имеет бесконечный разрыв в точке с отрезка [а, b] и непрерывна при и , то по определению полагают

Несобственный интеграл (где f (с)= ∞, a < с < b) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них.

Например, вычислим

Найдем

т. е. несобственный интеграл сходится.

6.8. Применение определенного интеграла в экономике

Пусть влияние различных факторов на изменение производительности труда описывается функцией Кобба-Дугласа вида

где функции A(t), L(t), K(t) – величины затрат природных ресурсов, труда и капитала; а₀, α, β, γ – некоторые числа.

Если в функции Кобба-Дугласа считать, что затраты труда есть линейная зависимость от времени, а затраты капитала неизменны, то она примет вид

.

Тогда объем выпускаемой продукции за время Т лет составит

.

Например, найдем объем продукции, произведенной за первый месяц, если изменение производительности выпуска продукции с течением времени от начала внедрения нового технологического процесса задается функцией f (t) = 32 – 2^-0,5t+5, где t – время в месяцах.

Pадаyf функция Кобба-Дугласа: f (t) = 32 – 2^-0,5t+5.

Используя экономический смысл определенного интеграла, получаем, что объем продукции u(t), произведенной за промежуток времени [0,1], вычисляется следующим образом:

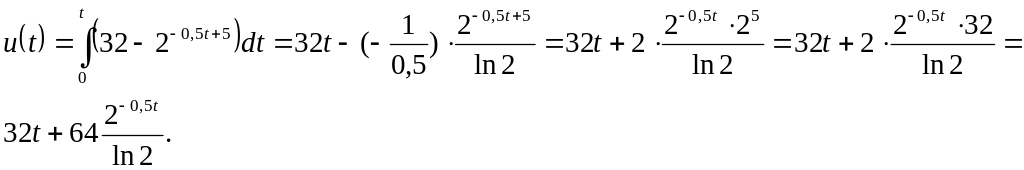
Тогда при t=1, получим .

Примеры решения задач к главе 6

Пример 6.1. Вычислить .

Решение. Первообразную подынтегральной функции найдем, используя формулу (9). Применяя формулу Ньютона-Лейбница, получаем

Пример 6.2. Вычислить .

Решение. Первообразную подынтегральной функции найдем, используя формулу (9).По формуле Ньютона – Лейбница получаем

.

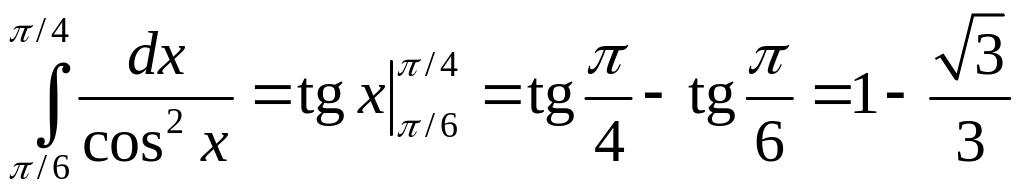Пример 6.3. Вычислить .

Решение. Воспользуемся методом интегрирования по частям. Положим откуда . Тогда

.

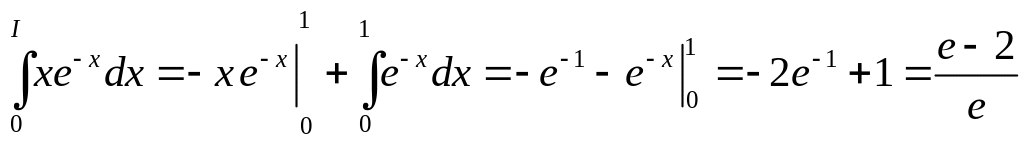Пример 6.4. Вычислить

Решение. Воспользуемся методом замены переменной.

Положим ; тогда ; если ,то ; если , то .

Следовательно,

.

Пример 6.5. Вычислить .

Решение. Подынтегральная функция – четная, а потому .

Интегрируем по частям, полагая ; тогда .

Отсюда находим

.

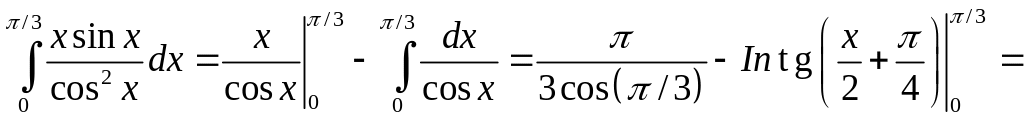
Следовательно, .

Пример 6.6. Найти несобственный интеграл

Решение. Подынтегральная функция – четная, поэтому

Тогда

.

Таким образом, т. е. несобственный интеграл сходится.

Пример 6.7. Найти несобственный интеграл

Решение. Подынтегральная функция f(x) = 1/x в точке x = 0 неограничена, а потому имеем

т. е. несобственный интеграл расходится.

Пример 6.8. Найти несобственный интеграл

Решение. Имеем

т. е. несобственный интеграл сходится.

Здесь использовали внесение под знак дифференциала.

Пример 6.9. Найти площадь фигуры, ограниченной параболой y=4x – x²

и осью Оx.

Решение. Парабола пересекает ось Оx в точках О(0; 0) и М (4; 0).

Следовательно,

S =

Пример 6.10. Найти площадь фигуры, ограниченной параболой у = (х – 1)²

и гиперболой х² – y²/2=1.

Решение. Найдем точки пересечения параболы и гиперболы, для чего решим совместно уравнения этих кривых:

х² – или х⁴– 4х³ + 4х² – 4х + 3 = 0.

Левую часть последнего уравнения можно разложить на множители:

(х – 1) (х–3) (х² + 1) = 0, откуда x₁=l, x₂ = 3 и y₁ = 0, y₂ = 4. Таким образом,

заданные кривые пересекаются в точках А (1;0) и В (3;4).

Следовательно,

S=

=

=

Пример 6.11. Найти длину дуги кривой x = cos⁵t, y = sin⁵ t от t₁ = 0 до

t₂ = р/2.

Решение. Найдем производные по параметру t:

х = –5 cos⁴ t sin t, y=5 sin⁴ t cos t.

Следовательно,

Пример 6.12. Найти площадь фигуры, ограниченной линиями у = – х²,

у = х – 2, у = 0.

Решение. Построим графики заданных функций.

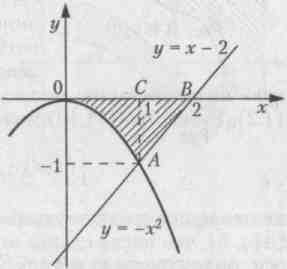
Из построения следует, что искомая площадь S криволинейного треугольника ОAВ может рассматриваться как площадь над кривой ОAВ на отрезке [0; 2]. Однако указанная кривая (ломаная) не задается одним уравнением. Поэтому для нахождения S = S_ОAB разобьем криволинейный треугольник ОАВ на части, проецируя точку А излома на ось абсцисс. Тогда S = S_OAC + S_AB.

Абсциссы точек О, А, В задают пределы интегрирования.

! Проверьте самостоятельно, что координаты точек О, А, В равны соответственно (0; 0), (1; –1), (2; 0).

S_OАC

S_АВC

Окончательно S = (ед.²).

Пример 6.13. Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями у = е^-x, у = 0, х = 0, х = 1 вокруг оси Ох.

Решение. Построим графики заданных функций.

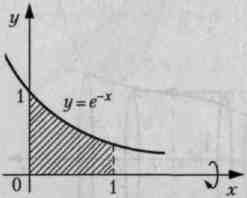
Искомый объем

(ед.³).

Пример 6.14. Найти объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями у = х², у = х³.

Решение. Построим графики заданных функций.

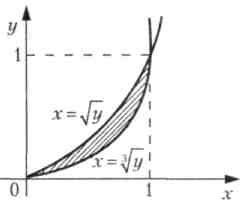
Проецируя вращаемую фигуру на ось ординат (ОУ), убеждаемся, что искомый объем V равен разности двух объемов: объема V_y1, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями х = , х = 0, у = 1, и объема V_y2, который образуется от вращения фигуры, ограниченной линиями х = ,

х = 0, у = 1.

Тогда

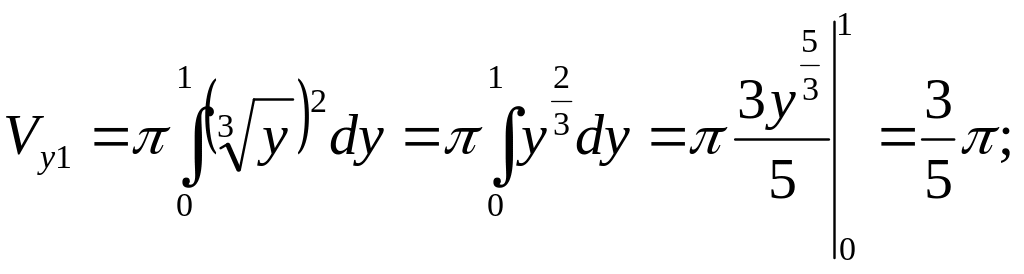
Окончательно имеем

(ед.³).