Глава 6. Определенный интеграл

6.1. Понятие определенного интеграла

Пусть на [а, b] задана функция у = f(x). Разобьем отрезок [а, b] на п элементарных отрезков точками х₀, x₁, ..., х_п: а = х₀ < х₁ < х₂ < ... < х_п = b. На каждом отрезке [x_i-1, x_i] разбиения выберем некоторую точку ξ_i и положим

∆х_i = x_i – x_i-1, где i = 1, 2, ..., п.

Сумму вида

называют интегральной суммой для функции у = f(x) на отрезке [а, b].

Очевидно, что интегральная сумма зависит как от способа разбиения [а, b] точками х₀, x₁, ..., х_п, так и от выбора точек ξ₀, ξ₁,..., ξ_n на каждом из отрезков разбиения [x_i-1, x_i], i =1, 2, ..., п.

Определенным интегралом от функции на отрезке (или в пределах от до ) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

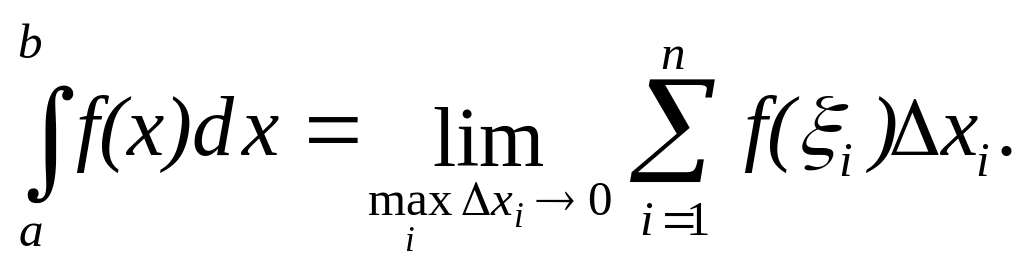
При этом число а называется нижним пределом, число b – верхним пределом интеграла; функция f(x) – подынтегральной функцией, выражение f(x)dx – подынтегральным выражением, а задача о нахождении – интегрированием функции f(x) на отрезке [а, b].

Геометрический смысл определенного интеграла.

Если на , то определенный интеграл геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями .

Экономический смысл интеграла.

Пусть функция z = f(x) описывает изменение производительности некоторого производства с течением времени. Найдем объем продукции и, произведенной за промежуток времени [0, Т].

Учитывая определение определенного интеграла, получаем

т.е. если f(t) – производительность труда в момент t, то – объем выпускаемой продукции за промежуток [0, Т].

Достаточное условие существования определенного интеграла (интегрируемости функции).

Если функция у = f(x) непрерывна на отрезке [а, b], то она интегрируема на этом отрезке.

6.2. Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла, т.е.

где α – некоторое число.

2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций, т.е.

.

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b, с

.

4. Если на отрезке [а, b] f(x) ≤ g(x), то и

,

т.е. обе части неравенства можно почленно интегрировать.

Следствие. Пусть на отрезке [а, b] m ≤ f(x) ≤ М, где т и М – некоторые числа. Тогда

.

5. Теорема о среднем. Если функция у = f(x) непрерывна на отрезке [а, b], то найдется такое значение ξ [а, b], что

6.3. Формула Ньютона-Лейбница

Теорема. Пусть функция у = f(х) непрерывна на отрезке [а, b] и F(x) – любая первообразная для f(x) на [а, b]. Тогда определенный интеграл от функции f(x) на [а, b] равен приращению первообразной F(x) на этом отрезке, т.е.

Полученная формула называется формулой Ньютона-Лейбница.

Вычисление определенных интегралов с использованием формулы Ньютона-Лейбница осуществляется в два шага.

На первом шаге, используя технику нахождения неопределенного интеграла, получают некоторую первообразную F(x) для подынтегральной функции f(x).

На втором применяется формула Ньютона-Лейбница.

Например, вычислим .

Первообразная для функции f(x) = х² имеет вид F(x) = + C.

Для нахождения интеграла по формуле Ньютона-Лейбница возьмем такую первообразную, у которой С = 0 (см. замечание выше). Тогда

Замечание.

Таким образом, при применении формулы Ньютона-Лейбница несущественно, какой из пределов интегрирования больше: верхний или нижний.