15.Найбільше і найменше значення функції на відрізку
Розглянемо
функцію
,
що є визначеною і неперервною на
відрізку 
.
До цього часу ми займались відшуканням
лише локальних максимумів і мінімумів.
Поставимо тепер задачу про
відшукання глобального
максимуму і глобального
мінімуму (global maximum and minimum),
або, іншими словами, відшуканню найбільшого
і найменшого значень
на
відрізку
.
Зазначимо, що неперервна функція, в силу
другої теореми Веєрштрасса, обов’язково
досягне в деякій точці відрізка
свого
найбільшого (найменшого) значення.
Найбільше (найменше) значення функція може приймати або у внутрішній точці відрізка (тоді воно збігається з одним із локальних екстремумів функції ), або на одному з кінців даного відрізка.
Звідси зрозуміло, що для знаходження найбільшого М і найменшого m значень неперервної функції на відрізку потрібно:
1) знайти критичні точки, які належать відрізку ;
2) обчислити значення функції в цих критичних точках і в точках a і b;
3) з усіх отриманих значень вибрати найбільше М і найменше m і відмітити точки, в яких ці значення досягаються.
Скорочено
записують так: 
.
Читають – найбільше значення (глобальний
максимум) функції
на
відрізку
дорівнює М і
досягається в точці 
.
Аналогічно 
.
Відшукання найбільшого (найменшого) значення функції неперервної на інтервалі, півпрямій, прямій проводиться подібним до вищенаведеного способом.
Приклад
3.35. Знайти
найбільше і найменше значення функції 
на
відрізку 
.
Розв’язування. Знаходимо похідну:
.
Прирівнюємо її до нуля:
.
Розв’язавши
це рівняння отримаємо критичні точки: 
,
причому 
.
Обчислимо значення функції в критичних
точках 
і 
,
а також на кінцях відрізка 
.
.
Отже 
, 
.
Відмітимо, що у випадку, коли неперервна функція має на відрізку лише одну точку локального максимуму (мінімуму), то можна стверджувати, що це і є точка глобального максимуму (мінімуму).
16. Поняття первісної функції та невизначеного інтеграла. Властивості невизначеного інтеграла.
Нехай функція f (x) задана на інтервалі (a,b) .
Функція F(x) називається первісною для функції f (x) ,
якщо для будь-якого x∈(a,b) виконується рівність F′(x) = f (x) .
Наприклад, нехай f (x) = cos x , тоді її первісна F(x) = sin x .
Дійсно, за означенням первісної: F′(x) = (sin x)′ = cos x = f(x).
Легко помітити, що функція 1F (x) = sin x + C (С - довільна стала) буде теж
первісною для функції f (x) = cos x :
F1 ′(x) = (sin x + C)′ = (sin x)′ + C′= cos x = f(x).
ТЕОРЕМА (про існування первісної).
Якщо функція f (x) неперервна на деякому інтервалі, то
для цієї функції існує первісна (а тому - і невизначений ін-
теграл).
Невизначений:
Означення. Якщо F(x) первісна для функції f (x) , то вираз F(x) + C ,
де С може приймати будь-яке стале значення, називається
невизначеним інтегралом від функції f (x) і позначається
символом
∫f (x)dx ,
де ∫- позначення інтегралу, f (x) - підінтегральна функція,
f (x)dx - підінтегральний вираз.
З геометричної точки зору невизначений інтеграл - це сім’я кривих (інте-
гральних кривих), кожна з яких отримується шляхом зсуву однієї з кривих
паралельно самій собі угору або вниз вздовж осі Оy.
Операція знаходження невизначеного інтеграла (тобто відшукання
F(x) + C ) від даної функції f (x) називається інтегруванням функції f (x) .
Властивості невизначеного інтеграла.
1. Невизначений інтеграл від диференціала деякої функції дорівнює
цій функції плюс довільна стала
∫dF(x) = F(x) + C .
Доведення: Нагадаємо, що диференціал функції y = f (x) знаходиться
за формулою : dy = f ′(x)dx , тому
∫dF(x) = ∫F′(x)dx = ∫f (x)dx =F(x) + C .
2. Диференціал від невизначеного інтеграла дорівнює підінтеграль-
ному виразу
d ∫ f (x)dx = f (x)dx .
Доведення:
d ∫ f (x)dx = d(F(x) + C) = dF(x) + dC = F′(x)dx + 0 = f (x)dx .
3. ∫c ⋅ f (x) dx = c ⋅ ∫ f (x)dx , де c ≠ 0 , тобто сталий множник можна
виносити за знак інтеграла.
4. ∫[ f1 (x) + f2 (x)] dx =∫f1 (x)dx +∫f2 (x)dx ,
тобто невизначений інтеграл від суми функцій дорівнює сумі неви-
значених інтегралів від цих функцій.
5. Якщо ∫f (x)dx = F(x) + C , то
∫f(ax+b)dx=
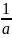F(ax+b)+C, де
a і
b
сталі
,(a
≠
0).
17. Таблиця основних інтегралів.
