10. Похідні та диференціали вищих порядків

(higher derivative, higher-order differential)

 

Нехай функція   диференційовна на проміжку X, а    її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної   називається похідною другого порядку (second-order derivative) функції   і позначається одним із символів:

.

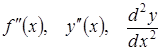 Так у фізиці, якщо    закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то   є прискоренням (acceleration) цієї точки в момент часу t.

 Аналогічно 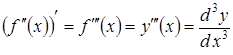  і т. д.

 Взагалі похідною n-го порядку від функції   називається похідна від похідної  -го порядку і позначається

  , або  , або  .

 Зауваження. При  , похідну n-го порядку позначають відповідно  ; при   позначають:   або  .

Приклад 3.17. Знайти похідну другого порядку від функції

 

.

Розв’язання. Знаходимо спочатку   за формулою  .

 

 

.

 

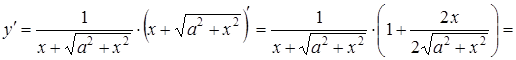
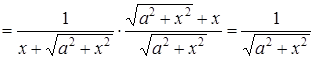Знаходимо похідну від отриманої функції:

 

 

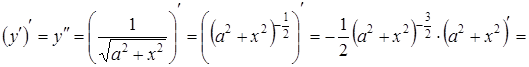
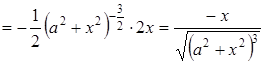, тобто  .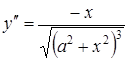

 Приклад 3.18. Знайти похідну n-го порядку від функції  .

Розв’язання.

.

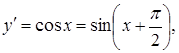
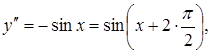
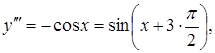
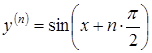Формула Лейбніца. Якщо функції  ,   мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:

.         (3.14)

 Похідні вищих порядків від функцій, заданих параметрично. Якщо функції   і   параметрично задають функцію  , то похідні 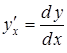 ,  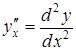, можна послідовно обчислити за формулами:

 

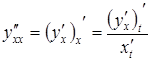,   і т. д.

 Так, для похідної другого порядку має місце формула:

 

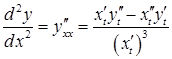.                               (3.15)

Приклад 3.19. Знайти похідну   функції  , заданої параметрично:  ,  .

Розв’язання.

.

 за формулою (3.15)

  .

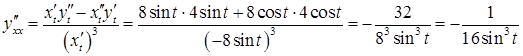 Диференціали вищих порядків. Нехай функція   диференційовна на проміжку X. Її диференціал

 називається також диференціалом першого порядку і його можна розглядати як функцію змінної x(приріст аргументу   вважається сталим).

Означення 3.4. Диференціалом другого порядку (second differential) функції   в точці xназивається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім  ) і позначається  :

 

.

 За означенням маємо

,

 позначають  . Таким чином

  .                                     (3.16)

 Аналогічно, диференціалом n-го порядку (позначається  ), n=2,3,... називається диференціал від диференціала порядку   за умови, що в диференціалах весь час беруться одні й ті самі прирости   незалежної змінної x. Тобто

  .

 При цьому справедлива формула:

  .                                     (3.17)

  Приклад 3.20. Обчислити  , якщо  .

Розв’язання. Скористаємось формулою (3.16). Для цього знайдемо  :

,  .

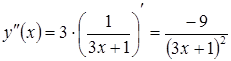 Отже

.

11.Правила Лопіталя розкриття невизначеностей (l'Hospital rule)

 

Теорема 3.10. (І правило Лопіталя). Якщо:

1) функції   і   диференційовні на інтервалі  ,   для всіх  ;

2)  ;

3) існує скінченна або нескінченна границя  ,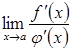

то існує границя 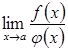 , причому має місце рівність:

 

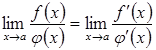.                              (3.21)

 

Доведення. Довизначимо функції   і   в точці   так, щоб вони стали неперервними, тобто покладемо  . Тепер   ці функції на відрізку  , ( ) задовольняють умови теореми Коші. Тому існує точка с,  , ( ) така, що

.

 

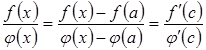Оскільки  , ( ) то  . Перейшовши в останній рівності до границі, за умови  , отримаємо

 

 що і потрібно було довести.

 

Запам’ятай добре! Доведену теорему зазвичай називають правилом Лопіталя розкриття невизначеності   за умови  .

Аналогічні теореми мають місце для розкриття невизначеності   у випадку односторонніх границь при  ,  .

 

Приклад 3.24. Обчислити границю  .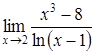

Розв’язання. Ми маємо невизначеність типу  . Функції   і   задовольняють умови теореми в деякому околі точки  . Застосуємо правило Лопіталя:

 

.

 

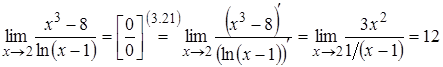Наслідок 1. Теорема Лопіталя справедлива також при  , при   і при  .

 

Приклад 3.25. Обчислити границю  .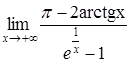

Розв’язання. Маємо невизначеність типу  . Застосуємо правило Лопіталя:

.

 

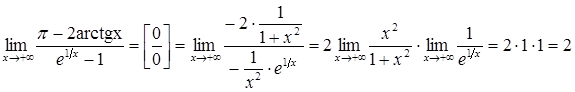Наслідок 2. Якщо похідні   і   задовольняють ті самі вимоги, що і функції   і  , то правило Лопіталя можна застосувати повторно. При цьому отримаємо

 

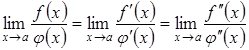.                       (3.22)

 

І взагалі, правило Лопіталя при виконанні умов теореми можна застосовувати багаторазово.

 

Приклад 3.26. Обчислити границю  .

Розв’язання. Дана границя дозволяє використовувати формулу (3.21) багаторазово, дійсно:

 

.

 

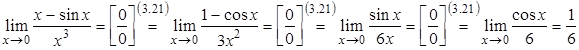Наслідок 3. Якщо в теоремі замінити умову 2) на наведену нижче

2)  , або  , то формула (3.21) також має місце.

В цьому випадку правило Лопіталя застосовується для розкриття невизначеності типу  ( ІІ правило Лопіталя).

 

Приклад 3.27. Якщо  , то

 

,

 

тобто довільний додатний степінь x зростає швидше, ніж   при  .

Розв’язування. Дійсно, застосувавши ІІ правило Лопіталя, отримаємо

 

.

 

Зазначимо, що формули (3.21), (3.22) мають місце лише тоді, коли існує скінченна або нескінченна границя  . Але буває і так, що границя 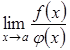  існує, у випадку коли границя   не існує.

 

Приклад 3.29.   існує і дорівнює  .

Розв’язання. Дійсно

 

.

 

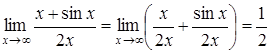Але відношення похідних 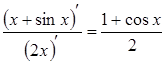  не має границі при  .

 

Після певних перетворень правило Лопіталя може бути застосовано також до розкриття інших невизначеностей, таких як:  ,  ,  ,  ,  .

Так, границі невизначеностей типів   та   доцільно звести до виду   або  .

 

Приклад 3.30. Обчислити границю  .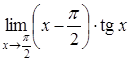

Розв’язання. Маємо невизначеність типу  . Приведемо цю невизначеність до виду   і застосуємо правило Лопіталя.

 

.

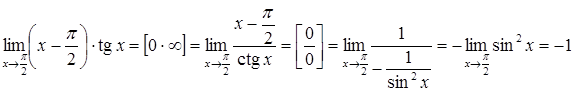 При розкритті невизначеностей типу  ,  ,   за допомогою правила Лопіталя попередньо необхідно виконати деякі перетворення.

Нехай треба обчислити границю складеної степеневопоказникової функції:

,

 

де ми маємо невизначеність одного з вищезгаданих типів. Запишемо цю границю у вигляді

,

 

тут в показнику маємо вже невизначеність виду  , яку можна звести до невизначеності типу   або   шляхом знесення в знаменник одного із співмножників, що стоять під знаком границі.