1.1.4С оединение треугольником

Е

Рисунок 4.9. Трехпроводная трехфазная цепь при соединении нагрузки треугольником

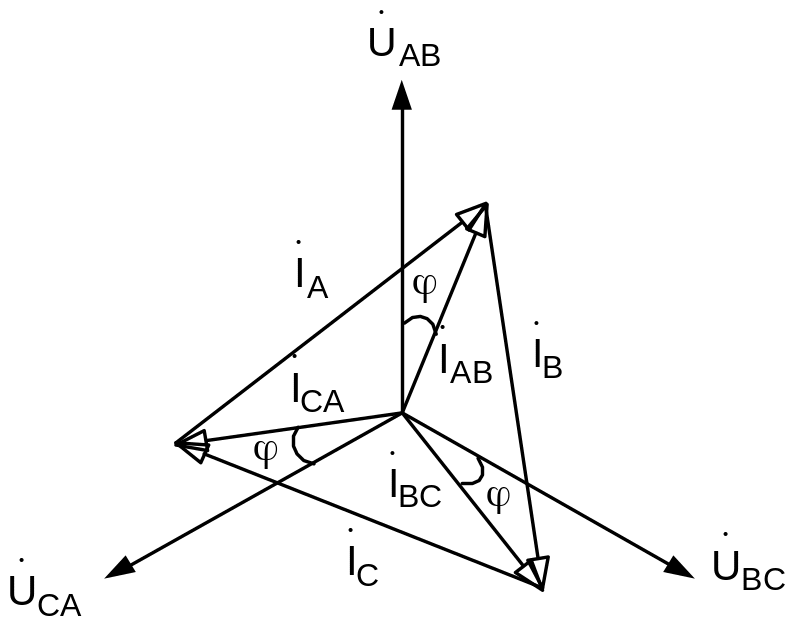
Рисунок 4.10. Векторная диаграмма для симметричной нагрузки, соединенной треугольником

сли три фазы нагрузки с фазными сопротивлениями , и включить непосредственно между линейными проводами трехпроводной трехфазной цепи, то получим соединение приемников треугольником (рис.4.9). Из схемы на рис.4.9 видно, что если пренебречь сопротивлениями линейных проводов, то фазные напряжения приемника всегда будут равны соответствующим линейным напряжениям источника: . В отличие от соединения звездой фазные и линейные токи не равны между собой. На схеме рис.4.9 условно положительные направления фазных токов , , соответствуют принятым условно положительным направлениям линейных напряжений , , . Если сопротивления фаз нагрузки заданы, то фазные токи определяются по формулам:

,

,

.

Линейные токи определяются по первому закону Кирхгофа для узлов а, b, c:

, , .

П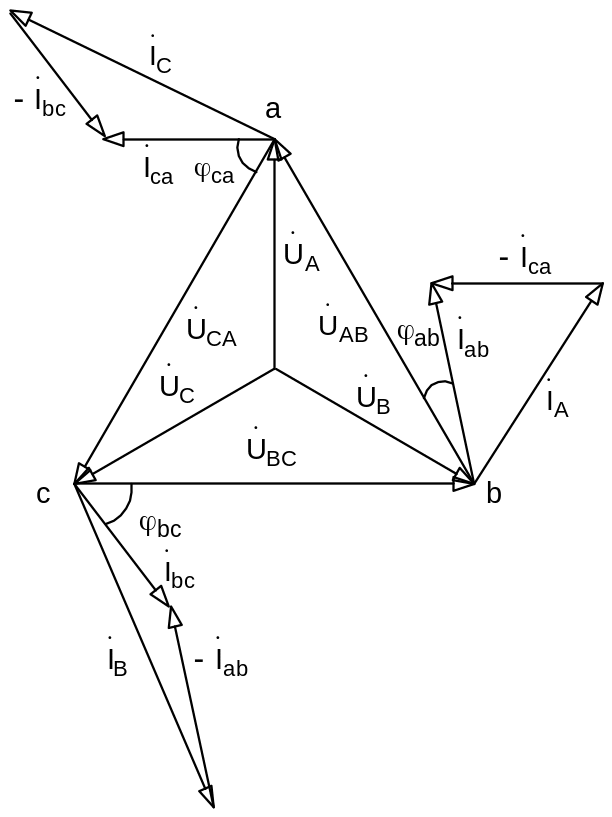 ри симметричной нагрузке = = фазные токи равны по величине и сдвинуты по фазе относительно соответствующих фазных напряжений на один и тот же угол. Векторная диаграмма напряжений и токов при симметричной нагрузке, соединенной треугольником показана на рис.4.10. Из диаграммы следует, что при симметричной нагрузке фазные и линейные токи связаны между собой зависимостью:

Рисунок 4.11. Векторная диаграмма для несимметричной нагрузки, соединенной треугольником

.

При несимметричной нагрузке фазные напряжения на нагрузке, соединенной треугольником остаются неизменными и равными соответствующим линейным напряжениям источника. Фазные токи определяются по тем же формулам, что и при симметричной нагрузке, но вследствие несимметрии нагрузки векторы токов уже не образуют симметричную систему. Для определения линейных токов можно воспользоваться уравнениями, составленными для узлов a, b, c по первому закону Кирхгофа или векторной диаграммой. Топографическая векторная диаграмма фазных напряжений на нагрузке и векторная диаграмма фазных и линейных токов показаны на рис.4.11. Из этой векторной диаграммы следует, что независимо от характера нагрузки геометрическая сумма векторов линейных токов в трехпроводной цепи равна нулю: .

Важной особенностью соединения фаз нагрузки треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным. Будет изменяться только ток данной фазы и линейные токи в линейных проводах, соединенных с этой фазой.

1.1.5Мощность трехфазной цепи

Активная мощность трехфазной цепи равна сумме активных мощностей потребляемых каждой фазой нагрузки:

.

При симметричной нагрузке мощности, потребляемые каждой фазой нагрузки равны. В этом случае , а мощность, потребляемая каждой фазой определяется как: .

где  - угол сдвига между фазным напряжением и током.

Реактивная мощность трехфазной цепи равна сумме реактивных мощностей отдельных фаз:

.

При симметричной нагрузке реактивные мощности отдельных фаз равны и реактивная мощность трехфазной цепи , реактивная мощность одной фазы: .

Полная мощность трехфазной цепи равна сумме полных мощностей отдельных фаз: .

При симметричной нагрузке полная мощность трехфазной цепи , полная мощность одной фазы: .

При анализе трехфазных цепей удобно пользоваться линейными значениями напряжений и токов. При соединении нагрузки звездой:

и .

При соединении нагрузки треугольником:

и .

В соответствии с этими выражениями, активная мощность трехфазной цепи, независимо от способа соединения нагрузки определяется по формуле:

.

А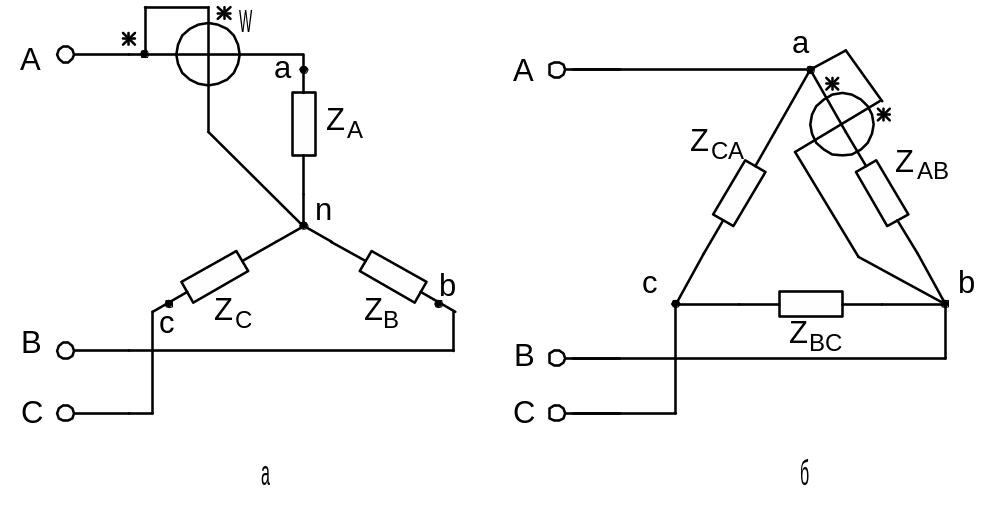 налогично определяется реактивная и полная мощность:

Рисунок 4.12. Измерение активной мощности в симметричной трехфазной цепи

, .

П

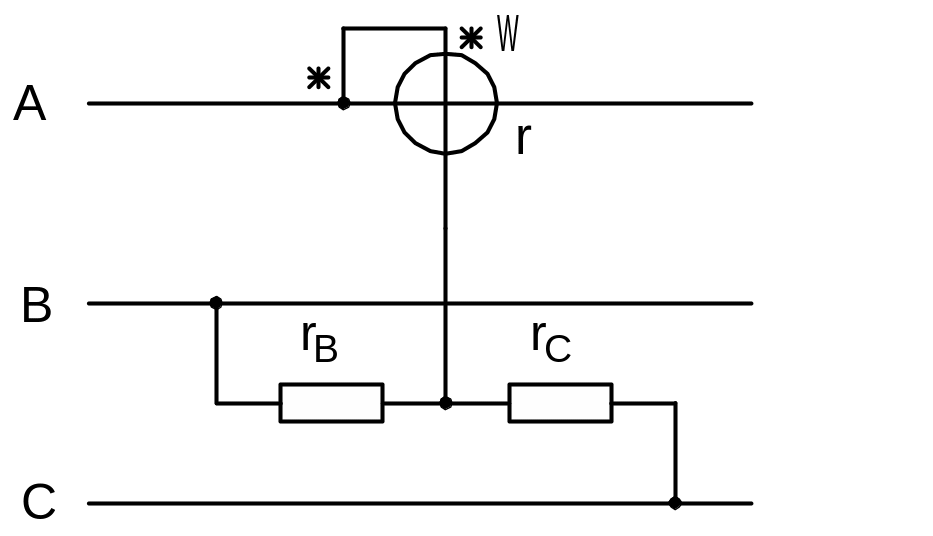
Рисунок 4.13. Схема с искусственной нейтральной точкой

ри симметричной трехфазной нагрузке активные мощности всех фаз одинаковы, поэтому достаточно измерить активную мощность одной фазы. Активная мощность трехфазной нагрузки . На рис.4.12 показаны схемы включения ваттметра для измерения активной мощности одной фазы при соединении нагрузки звездой с доступной нейтральной точкой (рис.4.12, а) и треугольником (рис.4.12, б). Если фазные напряжения и токи симметричной нагрузки недоступны для измерения, то применяют схему с искусственной нейтральной точкой (рис.4.13). В этой схеме цепь напряжения ваттметра с сопротивлением и два резистора образуют симметричную трехфазную нагрузку. Поэтому напряжение на ваттметре равно фазному напряжению нагрузки, соединенной звездой, или в раз меньше фазного напряжения нагрузки, соединенной треугольником. Ток, протекающий по токовой обмотке ваттметра, равен линейному току и равен фазному току нагрузки, соединенной звездой, или в раз больше фазного тока нагрузки, соединенной треугольником. Следовательно ваттметр независимо от способа соединения нагрузки измеряет активную мощность одной фазы.

Для измерения активной мощности несимметричной трехфазной нагрузки можно применять схемы описанные выше. Так как при несимметричной нагрузке мощности фаз не равны, то необходимо измерять мощность каждой фазы (то есть включать ваттметры в каждую фазу аналогично рис.4.12). Активная мощность несимметричной трехфазной нагрузки определяется как сумма мощностей отдельных фаз: . В схеме с искусственной нулев ой точкой мощность показываемая ваттметром, включенным в линейные провода фаз А, В, С ( , , ) не равна мощности соответствующих фаз, однако сумма показаний ваттметров равна мощности потребляемой несимм

Рисунок 4.14. Метод двух ваттметров

етричной трехфазной нагрузкой .

Чаще всего для измерения мощности в трехфазных трехпроводных цепях с несимметричной нагрузкой используют метод двух ваттметров, включенных в соответствии со схемой на рис.4.14. При этом активная мощность несимметричной трехфазной нагрузки равна алгебраической сумме (показания ваттметров могут быть отрицательными) показаний двух ваттметров.