3.4. Методы качественного оценивания систем

Методы оценивания систем делятся на качественные и количествен­ные. Качественные методы используются на начальном этапе моделирова­ния для создания концептуальной модели системы. Простейшей задачей оценивания является задача измерения. Более сложными являются задачи парного сравнения, ранжирования, классификации, численной оценки. Ре­шение задачи оценивания экспертом называется экспертизой. Основные методы качественного оценивания систем: - методы типа «мозговой атаки» или «коллективной генерации идей»;

37

• м етоды сценариев;

• экспертных оценок;

• метод Дельфи;

• дерево целей;

• морфологические методы.

Рассмотрим подробнее морфологические методы, основная идея кото­рых путём комбинирования выделенных элементов находить все мысли­мые варианты решения проблем. Впервые эти методы использовал Ф. Цвикки, подразделив их на метод систематического покрытия, метод от­рицания и конструирования и метод морфологического ящика (ШЛЯ). Наиболее широкое применение нашел ММЯ, особенно для анализа и раз­работки прогнозов в технике. Морфологический подход связан со струк­турными взаимосвязями между объектами. Он предполагает использова­ние полной совокупности знаний об объекте, поэтому его используют при наличии малого объёма информации. Необходимым требованием является отсутствие какого-либо предварительного суждения, при этом из рассмот­рения нельзя исключать объекты и процессы без предварительного анали­за. В отраслях экономики морфологические методы можно использовать при исследовании новых рынков потребностей при отсутствии аналогов.

К модификациям ММЯ относятся: метод организующих понятий; ме­тод десятичных матриц поиска; метод семикратного поиска. Комбинатор­ный метод также является усовершенствованием морфологического мето­да. Пример морфологической таблицы см. в таблице 4.

Таблица 4 — Морфологическая таблица мероприятий

Функция или мероприятие
Реконструкция предприятий	АН-ТЭЦ-3	А12 — Дальли-зель	AI3 - Хлебо­завод
Привлечение иностранных инвестиций	A2I - Завод По производ­ству автомо­билей	А22 - ЦБК
Развитие транспортной систе­мы	A31 - малая авиация	А32 - Троллей­бус	АЗЗ - Скоро­стной трамвай
Развитие системы образования	А41 - ПТУ и колледжи	А42 - Новые школы	А43 Педагогическое образование	А44 - Ат­тестация вузов

Анализ морфологических множеств может производиться различными методами. Методика исследования по различным сочетаниям критериев ничсства предполагает генерацию всех возможных вариантов систем и псих возможных парных тернарных и т.д. сочетаний критериев качества, мри этом для каждой альтернативы определяется её оценка по каждому критерию. Выбор лучшего варианта осуществляется сравнением вариантов между собой или с заданным образцом. Другой подход определяет крите-рИЙ комбинационной новизны, который даёт числовые характеристики но-Ш.1М сочетаниям функциональных подсистем.

Комбинаторно-морфологические методы в экономике эффективно применяются для решения задач функционально-стоимостного анализа и прогнозирования систем. В качестве примера продолжим рассмотрение морфологической таблицы 4. Для каждой альтернативы укажем оценку её 1ЫГОД В и оценку издержек И в условных единицах (см. таблицу 5).

Таблица 5 — Морфологическая таблица мероприятий с указанием иыгод и издержек

'Пункция или меро-		Альтернатива
|]1ИР1ТИС
'■Конструкция пред-	АН-ТЭЦ-3	А12-	А13-Хлебо-
фИЯТий	В =100	Дальдизель	завод
	И~40	В =50	В =10
		И --60	И =5
Иримличение ино-	А21 - Завод по	А22
фнпных инвестиций	производству ав-	ЦБК
	томобилей	В =70
	В= 100	И = 40
	И = 70
Гппнгше транспорт-	А31 - малая авиа-	А32	АЗЗ - Скоро-
Illlll UHCTCMb]	ция	Троллейбус	стной трам-
	В =100	В = 30	вай
	И =100	И =10	В = 25
			И =15
Гн'шитие системы об-	А4 ] - ПТУ и кол-	А42 - Но-	А43	А44 - Атте-
рцкшшпга	леджи	вые ШКОЛЫ	Педагогиче-	стация вузов
			ское образо-	В= 15
	В = 50	В = 10	вание	И =5
	И =40	И = 5	В = 20
			И =10

Анализировать таблицу 5 можно по различным критериям. Например, максимальную выгоду, равную 350, даёт вариант (All, A21, А31, А41),

II I I МЛ

II I I,

3 8

минимальные издержки, равные 60, имеют варианты (А 13, А22, А32 А42) и (А 13, А22, A32, А44). Обычно поиск рациональных вариантов в& дётся по максимальному отношению выгод к издержкам, при этом могут быть наложены дополнительные ограничения. Допустимыми решениями задачи

В/И-+тах И<80; В>300,

будут варианты (All, A21, А31, А41), (All, A22, А31, А41) и (А 12, А21, А31, А41), т.к. они удовлетворяют условиям, а поскольку отношения соответственно равны 1,40; 1,45 и 1,11, то максимальное значение достига­ется при втором варианте.

Аналогичные задачи можно решать и в том случае, когда точные зна­чения выгод и издержек неизвестны частично или полностью, но при этом известны их экспертные оценки. В этом случае для учёта особенностей функциональной подсистемы строится иерархия выгод (и (или) издержек), 3.5. Методы количественного оценивания систем

Задача количественного оценивания систем первоначально ставилась как задача нахождения максимальных значений параметров. Однако нали­чие неоднородных связей между показателями приводит к необходимости корректировки критерия превосходства, то есть требуется учет приемле­мых значений всех показателей. К методам количественной оценки отно­сятся: методы теории полезности; методы векторной оптимизации; методы ситуационного управления и инженерии знаний. При использовании дан­ных методов к реальным системам следует помнить, что:

• не существует системы, наилучшей в не зависящем от ЛПР смысле;

• не существует системы, оптимальной для всех целей и воздействий внешней среды;

• использование методов математического программирования обычно неэффективно в задачах оценивания сложных организационных систем.

При аксиоматическом подходе к оценке систем на основе теории по­лезности проверяются основные аксиомы: измеримости, сравнимости, транзитивности, коммутативности и независимости. Если все пять аксиом

39

1ЫП0ЛИЯЮТСЯ, то, согласно теории полезности, существует однозначно оп-р|ДвЛёИиВЛ функция полезности. Функция полезности является универ-61Л1ИЫМ И удобным средством математического выражения предпочтений ЛПР на множестве исходов операции. Поскольку точных методов опреде-Л^НИЯ полезности исхода операции не существует, то функцию полезности И1ХОДЯТ, используя экспертные оценки или методы аппроксимации или МОДМИруя систему более высокого уровня иерархии, включающую систе­му 0 иооледуемой операцией.

Методы векторной оптимизации используются для оценки систем в ус-ЛОВИЯХ определённости. Для исследуемой системы с помощью системного 1ИВЛИЗВ определяют частные показатели и критерии эффективности, по-ТОМ находят множество Парето и формулируют задачу многокритериаль­ной оптимизации, заменяют векторный критерий скалярным на основе ка-КОЙ'ЛИбо функции свёртки и решают задачу оптимизации на множестве Пврето о полученным скалярным критерием. Способ свёртки зависит от Характера показателей и целей оценивания системы. Общим случаем функции СВЙртки (агрегирования, осреднения) является средняя степенная функция

ГДв р — показатель, отражающий допустимую степень компенсации МАЛЫХ значений одних равноценных показателей большими значениями других показателей.

При р ^Ш1 эта функция совпадает с функцией аддитивной свертки, при р—* 0 она превращается в функцию мультипликативной свертки, а При р —>- оо получается функция свертки, которая не допускает никакой компенсации и требует равномерное подтягивание всех показателей к наи-Лучшему уровню. В критериях оценки экономических систем часто ис-ПОЛЬЗуют функцию агрегирования в виде отношения одних показателей , •ыражающих целевой эффект, к другим, связанным с затратами на дости­жение цели. К методам решения задач многокритериальной оптимизации относятся: метод выделения главного критерия, метод лексикографической оптимизации, метод последовательных уступок, человеко-машинные про-

4 0

цедуры векторной оптимизации. Главным недостатком этих методов явля ется неопределенность условий их применимости, что вызвано эвристиче ским характером самих методов.

В условиях риска однозначность соответствия между системами и ис ходами операции нарушается, поэтому эффективность систем в вероятно стных операциях находится через математическое ожидание функции по> лезности на множестве исходов. Кроме оптимизации «в среднем» исполь зуются критерии: максимум вероятности случайного события, минимум дисперсии результата, минимум среднего риска и т.д.

В условиях неопределённости для большого класса задач управления организационно- техническими системами часто отсутствуют объектив­ные критерии оценивания, а несводимость операций, проводимых такими системами, к детерминированным или вероятностным не позволяет ио пользовать для их оценки детерминированные и вероятностные критерии, В зависимости от характера неопределённости операции могут быть игро­вые и статистически неопределённые. В игровых операциях неопределён­ность вызывается действиями противника, а в статистически неопределён­ных противником является природа. Для исследования первых использует­ся теория игр, а для вторых - теория статистических решений. Для оценки уникальных операций используются субъективные предпочтения ЛПР, Обычно для оценки эффективности систем в условиях неопределённости используются таблицы, в которых указаны векторы управляемых парамет­ров, определяющие свойства системы, векторы неуправляемых парамет­ров, определяющие состояние обстановки, значения эффективности систе­мы для всех состояний обстановки и значения эффективности всех систем при одном и том же состоянии обстановки. Поскольку единого критерия оценки эффективности не существует, то используются основные требо­вания к процедурам оценки:

• оптимальное решение не зависит от перестановки строк и столбцов матрицы эффективности;

• оптимальное решение не меняется при добавлении тождественной строки (столбца) к матрице;

41

- оптимальное решение не меняется от увеличения каждого элемента матрицы на постоянное число;

• оптимальное решение не меняется при добавлении новых систем, ес­ ли Среди них нет более эффективных;

• если две системы являются оптимальными, то их вероятностная смесь Также оптимальна.

В зависимости от предпочтений ЛПР в неопределённых операциях ис-ПОЛЬзуются критерии среднего выигрыша, Лапласа, осторожного наблюда­теля (Вальда), максимакса, пессимизма- оптимизма (Гурвица), минималь­ного риска (Сэвиджа).

3i6> Метод анализа иерархий

Метод анализа иерархий используется для оценки последствий прини­маемых решений в иерархических системах планирования. Сами системы ООСТОЯТ из специфических элементов: фокус иерархии, акторы, цели, поли-ТИКИ, исходы и общий исход. В фокусе иерархии отражается общая цель; акторы - это действующие силы, влияющие на исходы; цели - желаемые Пределы или величины в планируемом решении; политики - разрешённые Средства достижения целей; исходы - потенциальные состояния системы (ПООЛе применения политик). Обобщённый исход интегрирует значения Отдельных исходов и определяет оценки.

Общая структура метода анализа иерархий может включать несколько Иерархических уровней, для каждого из которых определены свои крите­рии. Сложность метода заключается в определении весовых коэффициен-Т0> для оценки альтернатив. Если на данном уровне иерархии имеется к критериев, то требуется матрица парных сравнений к-oro порядка. В ней отражаются суждения ЛПР относительно важности каждого из этих крите­риев. Для сравнения используются числа от 1 до 9. Если критерии одина­ково важны, то соответствующий элемент матрицы равен 1 (т.е. все диаго­нальные элементы в матрице равны 1). Оценка 5 ставится, если критерий значительно важнее другого критерия, а оценка 9 — для чрезвычайно важ-НОГО по сравнению с другим. Остальные числа используются как промежу­точные оценки важности. Согласованность этих оценок обеспечивается

4 2

требованием, чтобы симметричный элемент матрицы равнялся обратном) числу, т.е. если

А мк = 3, то А км = -.

Для того чтобы полученную матрицу можно было использовать в ме> тоде, её следует нормализовать и проверить на согласованность. Если i нормализованной матрице получились одинаковые столбцы, то результи­рующие относительные веса не зависят от того, как выполнялось сравне­ние (матрицы 2x2 всегда согласованы).

Поскольку матрицы получаются на основе человеческих суждений, то столбцы в них обычно различные и требуется проверка на допустимый уровень рассогласованности. Условие согласованности матрицы

Ах = пх,

где х - собственный вектор матрицы А, п - собственное число матрицы А.

В методе анализа иерархий значения х и п находят приближённо, по­этому используется коэффициент согласованности

CR = CI/(RI), CI=(nmax-n)/(n-l), RI = 1,98 (п-2)/п.

Если CR< 0,1 , то уровень согласованности приемлемый и матрицу можно использовать для дальнейших расчётов; если CR> 0,1, то матрицу рекомендуется пересмотреть.

Пример метода анализа иерархий. Отделу кадров требуется выбрать сотрудника из трёх кандидатур К, Л, М, используя три критерия: собеседо­вание С, опыт работы О и рекомендации Р. Известны матрицы парных сравнений. В матрице А сравниваются критерии С, О и Р. В матрице Ас сравниваются кандидатуры К, Л, М по критерию собеседования С, в мат­рице Ао сравниваются кандидатуры по критерию опыта работы О и в мат­рице Ар сравниваются кандидатуры по критерию рекомендации Р.

2 Г

4

1 6 4

i 1 I 6 5

1 I I

2 5 4 5 1

А =

А,. =

43

1	1	2
	3
3	1	1
		2
1	2	1
Л

¹ 5 '

1 2 1

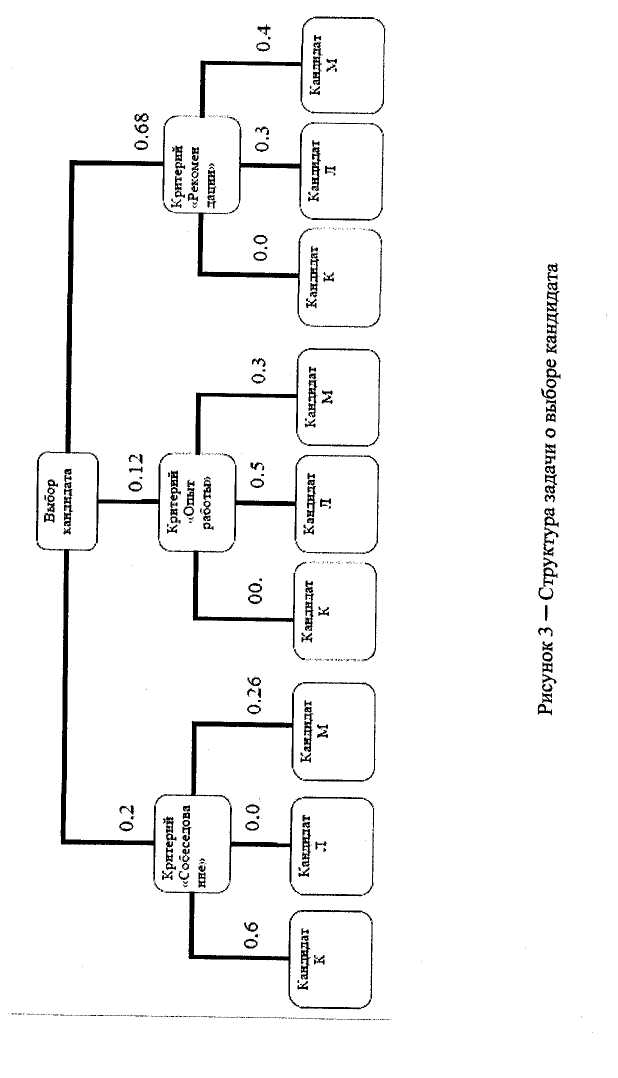
Требуется выполнить выбор кандидатуры, используя метод анализа . Структура задачи изображена на рисунке 3.

ДЛЯ определения весовых коэффициентов, указанных на этом рисунке, 1рвбувтся нормализовать данные матрицы А> А_с> А_о> А ^и проверить их

Ml Согласованность. Рассмотрим подробно нормализацию и проверку на •вГЛМОванность матрицы А- Для каждого столбца матрицы^ посчитаем

его элементов и в нормализованной матрице ffl_A в качестве элемен-ТОВ МШишем отношение каждого элемента к сумме элементов столбца, в НОТОром он находится. Для первого столбца сумма равна 5,5 (1+ % +4) и, Мр1Х0ДЯ к десятичным дробям, получаем элементы первого столбца: 0,181; 0,09; 0J29.

44

45

0,181 0,25 0,17 0,09 0,125 0,14

матри-

Аналогично находятся остальные столбцы N_A =

0,729 0,625 0,69, ЦЫ| Поскольку полученные столбцы матрицы ]\[_д существенно отличают-

61 Друг от друга, то требуется проверка матрицы на согласованность. Для •ТОГО вычисляем w (среднее значение в строчке).

we = (0,181 + 0,25 +0,17)/3 = 0,2; wo = 0,12 и wp = 0,68. Далее находим произведение матрицы Д и вектора w. Координаты по-

лучвнного вектора (0,58; 0,35; 2,08) определяют

п max = 3,01 (0,58 + 0,35 + 2,08), CI = (3,01 - 3)/2 = 0,005, RI = 1,98/3 = 0,66 и CR = 0,005/0,66 = 0,0076.

Полученное значение 0,0076 меньше 0,1, значит, матрица^ согласо-

ММИая, Для матриц Ас, Ао и Ар необходима аналогичная проверка, по-ОКОЛЬКу их нормализованные матрицы имеют разные столбцы.

'0,71 0,5 0,769^ ("0,25 0,143 0,4"

N_Al, = 0,116 0,083 0,057 ,N_Ar= 0,5 0,286 0,2 , [о,174 0,417 0,183 J [о,25 0,561 0,4,

'0,17 0,116 0,2^ч

N^' 0,5 0,79 0,4

[о,33 0,705 0,4,

Для матрицы Ас имеем п max = 3,13 и вектор (0,66; 0,08; 0,26); для МИрицЫ Ао имеем п max =3,15 и вектор (0,16; 0,53; 0,31); для матрицы Ар имеем п max = 3,12 и вектор (0,2; 0,33; 0,47). На основании этих зна-Ч1НИЙ матрица Ао имеет CR = 0,113 и, так как CR больше 0,1, то матрицу Ао требуется откорректировать. В данном примере вычисления продол-ЖМОТСЯ с исходной матрицей. Чтобы определить лучшую по данным кри-ТврИЯМ кандидатуру следует выбрать кандидата, набравшего максималь­ную оценку, зависящую от рассчитанных весовых коэффициентов. К: 0,2*0,66+0,68*0,2+0,12*0,16 = 0,27 Л: 0,2* 0,08+ 0,68*0.33+0,12*0,53 = 0,29 М: 0,2* 0,26+ 0,68*0,47+ 0,12*0,31 = 0,43.

II I

46

В данной задаче максимальное значение 0,43 и лучшей кандидатуре! является М, но этот вывод может измениться, если согласовать оценю парных сравнений в матрице Ао .