12. Теплові машини

1. ККД теплової машини знаходиться по формулі

1) ; 2) ; 3) .

2. ККД теплової машини знаходиться по формулі

1) ; 2) ; 3) .

3. ККД теплової машини знаходиться по формулі

1) ; 2) ; 3) .

4. Вираз для ККД справедливий

1) тільки для теплової машини, що працює по циклі Карно;

2) тільки для теплової машини, що працює на ідеальному газі;

3) для будь-якої теплової машини.

5. Вираз для ККД справедливий

1) тільки для теплової машини, що працює по циклі Карно;

2) тільки для теплової машини, що працює на ідеальному газі;

3) для будь-якої теплової машини.

6. ККД циклу Карно знаходиться по формулі

1) ; 2) ; 3) .

7. Для будь-якої теплової машини справедливе співвідношення

1) ; 2) ; 3) .

8. Для ідеальної теплової машини, що працює по циклі Карно

1) виконана робота менше теплоти, переданої нагрівачем;

2) виконана робота більше теплоти, переданої нагрівачем;

3) виконана робота дорівнює теплоті, переданої нагрівачем.

9. Для будь-якої теплової машини

1) виконана робота менше теплоти, переданої нагрівачем;

2) виконана робота менше теплоти, отриманої холодильником;

3) виконана робота менше теплоти, переданою нагрівачем і отриманою холодильником.

10. Цикл Карно складається з

1) двох ізохор і двох адіабат;

2) двох ізотерм і двох адіабат;

3) двох ізобар і двох адіабат.

11. Теплова машина 1/3 тепла, отриманого від нагрівача, віддає холодильнику. Чому дорівнює ККД такої машини?

1) 0,33; 2) 0,45; 3) 0,66.

12. Ідеальна теплова машина, що працює по циклі Карно 1/3 тепла, отриманого від нагрівача віддає холодильнику. Знайти температуру холодильника, якщо температура нагрівача дорівнює 27⁰С.

1) 100 ДО; 2) 133 ДО; 3) 166 ДО.

13. ККД теплової машини, що одержує від нагрівача 450 Дж тепла, і віддає холодильнику 140 Дж дорівнює

1) 0,31; 2) 0,46; 3) 0,69.

14. ККД ідеальної теплової машини, що має температуру нагрівача 450⁰С, і холодильника 60⁰С дорівнює

1) 0,36; 2) 0,46; 3) 0,64.

15. Ідеальна теплова машина, що працює по циклі Карно, має ККД 30%. Знайти температуру холодильника, якщо температура нагрівача дорівнює 300⁰С.

1) 372 ДО; 2) 401 ДО; 3) 472 ДО.

16. Що вигідніше для підвищення ККД ідеальної теплової машини

1) підвищити температуру нагрівача на 20⁰;

2) понизити температуру холодильника на 20⁰;

3) однаково.

17. ККД ідеальної теплової машини

1) дорівнює 1;

2) визначається температурами нагрівача й холодильника;

3) визначається тертям у машині.

18. Цикл Карно правильно показаний на рисунку

19. Цикл Карно правильно показаний на рисунку

20. Цикл Карно правильно показаний на рисунку

13. Друге начало термодинаміки. Ентропія

1. Оборотним називається процес, що задовольняє умові

1) після проходження процесу в навколишнім середовищі не повинне відбутися ніяких змін;

2) процес може йти в прямому й зворотному напрямках;

3) необхідне виконання обох умов.

2. Друге начало термодинаміки можна сформулювати так

1) неможливо побудувати теплову машину, що виконувала б роботу, більшу теплоти, отриманої від нагрівача;

2) неможливо побудувати теплову машину, що виконувала б роботу тільки за рахунок охолодження деякого тіла;

3) обидві формуліровки еквівалентні.

3. Друге начало термодинаміки можна сформулювати так

1) неможливо побудувати теплову машину, що виконувала б роботу, більшу теплоти, отриманої від нагрівача;

2) неможливий процес, єдиним результатом якого була б передача тепла від холодного тіла до гарячого;

3) обидві формуліровки еквівалентні.

4. Друге начало термодинаміки можна сформулювати так

1) неможливо побудувати теплову машину, що виконувала б роботу тільки за рахунок охолодження деякого тіла;

2) неможливий процес, єдиним результатом якого була б передача тепла від холодного тіла до гарячого;

3) обидві формуліровки еквівалентні.

5. Мікростан системи описується

1) набором термодинамічних параметрів системи;

2) набором координат і швидкостей всіх молекул;

3) обидві формуліровки еквівалентні.

6. Макростан системи описується

1) набором термодинамічних параметрів системи;

2) набором координат і швидкостей всіх молекул;

3) обидві формуліровки еквівалентні.

7. Термодинамічна ймовірність визначається

1) числом мікростанів, можливих для даного макростану;

2) числом мікростанів, можливих для даної температури;

3) числом мікростанів, можливих для даної енергії системи.

8. Ентропія замкнутої термодинамічної системи

1) не може зростати;

2) залишається постійною;

3) не може убувати.

9. При необоротних процесах ентропія

1) зростає;

2) убуває;

3) може зростати й убувати.

10. При оборотних процесах ентропія

1) залишається незмінною;

2) убуває;

3) може зростати й убувати.

11. Для оборотних процесів справедливо

1) ; 2) ; 3) .

12. Для необоротних процесів справедливо

1) ; 2) ; 3) .

13. При виконанні циклу Карно ентропія

1) зростає;

2) убуває;

3) не міняється.

14. Т ермодинамічна ймовірність зазначеного стану системи, що складається з 4 молекул, дорівнює

1) 2; 2) 4; 3) 6.

15. Т ермодинамічна ймовірність зазначеного стану системи, що складається з 4 молекул, дорівнює

1) 2; 2) 4; 3) 6.

16. Ентропія з термодинамічною ймовірністю зв'язана співвідношенням

1) ; 2) ; 3) .

17. Для оборотного процесу справедливе співвідношення

1) ; 2) ; 3) .

18. Для необоротного процесу справедливе співвідношення

1) ; 2) ; 3) .

19. Зміна ентропії при перетворенні 1 кг води в пару дорівнює

1) ; 2) ; 3) . .

Справка: питома теплота пароутворення води 2.3·10⁶ Дж/кг.

20. При , ентропія наближається до

1) 0; 2) 1; 3) .

Коливання й хвилі.

1. Коливаннями називаються

   1. рухи або процеси, яким притаманні ті або інші ступені повторюваності в часі;

   2. рухи або процеси, при яких система через рівні проміжки часу повертається у вихідний стан;

   3. рухи або процеси, яким притаманні ті або інші ступені повторюваності в просторі.

2. Коливання називаються періодичними, якщо

   1. рухи або процеси, які характеризуються тим або іншим ступенем повторюваності в часі;

   2. рухи або процеси, при яких система через рівні проміжки часу повертається у вихідний стан;

   3. рухи або процеси, які характеризуються тим або іншим ступенем повторюваності в просторі.

3. Періодом коливань називається

   1. час, протягом якого зсув від положення рівноваги двічі досягає того самого значення;

   2. час, протягом якого система виконує одне повне коливання;

   3. час, протягом якого зсув досягає амплітудного значення.

4. Періодичні коливання в загальному випадку описуються рівнянням

5. Гармонічними називаються коливання, у яких залежність зсуву від часу описується рівнянням:

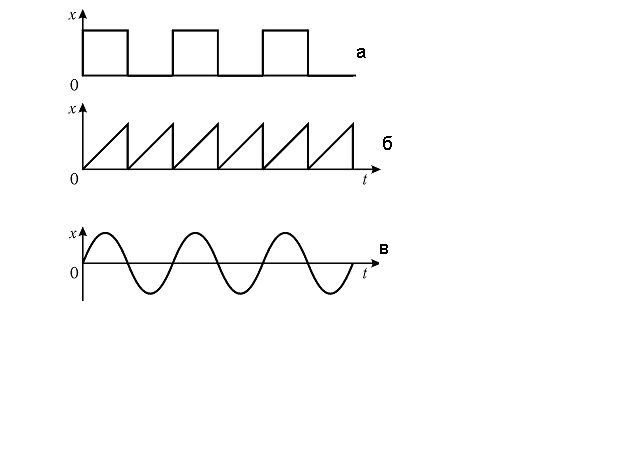
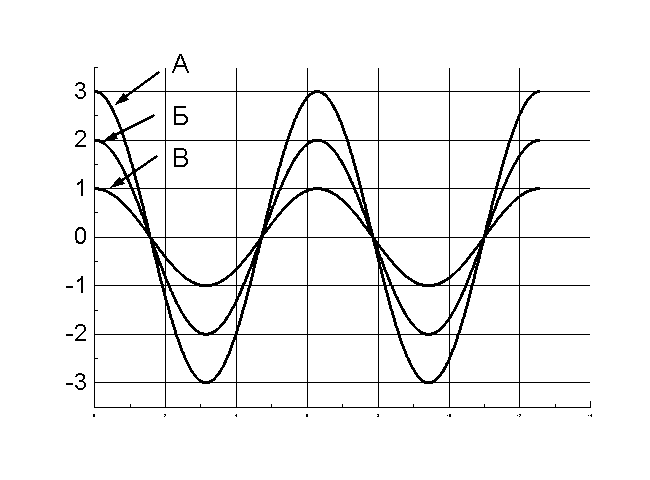
6. На рисунку показані три типи періодичних коливань. Укажіть, яке з них є гармонічним.

а в б

6. Амплітуда коливань - це

• шлях, пройдений матеріальною точкою від положення рівноваги до максимального відхилення;

• максимальне по модулі відхилення від положення рівноваги;

• обидві відповіді правильні.

7. Циклічна частота коливань чисельно дорівнює

• числу коливань за одиницю часу;

• числу коливань за час, рівний періоду коливань;

• числу коливань, виконаних за секунд.

8. Лінійна частота коливань чисельно дорівнює

• числу коливань, виконаних за одиницю часу;

• числу коливань за час, рівний періоду коливань;

• числу коливань, виконаних за секунд.

8. Герц - частота такого коливального руху, у якому

• за 1 с відбувається одне повне коливання;

• за с відбувається одне повне коливання;

• за час, рівний періоду коливань, відбувається одне повне коливання.

9. Період коливань - це

• час, за який відбувається одне повне коливання;

• час, за який зсув досягає максимального значення;

• час, за який матеріальна точка переходить зі стану рівноваги в стан з максимальним зсувом.

10. Між періодом коливань і лінійною частотою існує зв'язок

11. Фаза

• це – аргумент тригонометричної функції, що показує, яка частина коливання виконана до даного моменту часу, якщо повному коливанню зіставить значення ;

• показує зсув від положення рівноваги в початковий момент часу;

• це – аргумент тригонометричної функції, що показує, яка частина коливання виконана до даного моменту часу, якщо повному коливанню зіставить значення .

12. Початкова фаза

• це – аргумент тригонометричної функції, що показує, яка частина коливання виконана до даного моменту часу, якщо повному коливанню зіставить значення ;

• показує зсув від положення рівноваги в початковий момент часу;

• це – аргумент тригонометричної функції, що показує, яка частина коливання виконана до даного моменту часу, якщо повному коливанню зіставить значення .

13. Диференціальне рівняння гармонічних коливань має вигляд:

14. Диференціальне рівняння загасаючих коливань має вигляд:

15. Диференціальне рівняння вимушених коливань має вигляд:

15. Квазіпружна сила

• завжди спрямована до положення рівноваги, а її значення пропорційно зсуву від положення рівноваги:

• це один з видів потенційних сил:

• обоє твердження вірні.

16. Гармонічне коливання відбувається за законом косинуса із частотою ω₀, початковою фазою φ₀ і амплітудою А. При цьому швидкість змінюється за законом:

17. Гармонічне коливання відбувається за законом косинуса із частотою ω₀, початковою фазою φ₀ і амплітудою А. При цьому прискорення змінюється за законом:

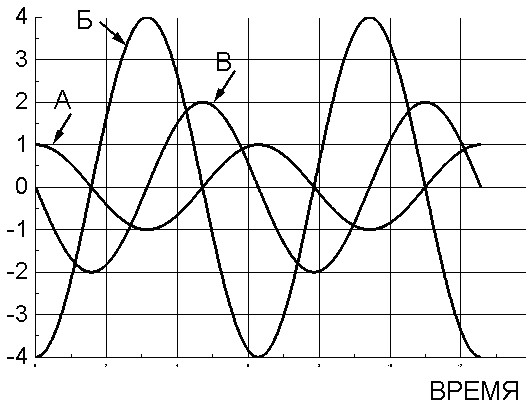
18. Гармонічне коливання відбувається за законом косинуса із частотою ω₀=1рад/с, початковою фазою φ₀=0 і амплітудою А=1. Укажіть графік залежності швидкості від часу.

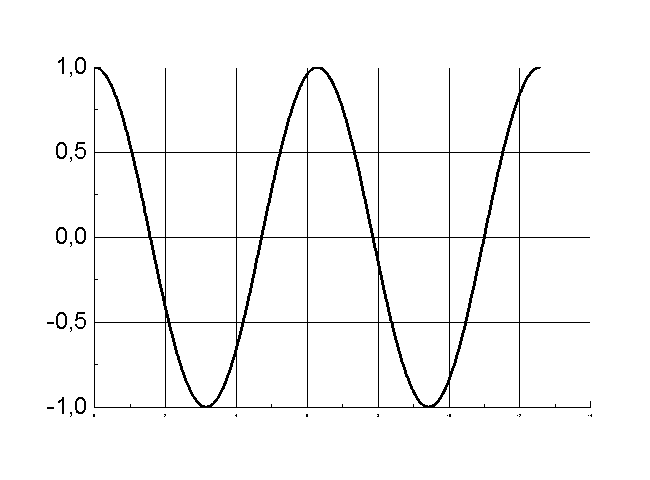
    А

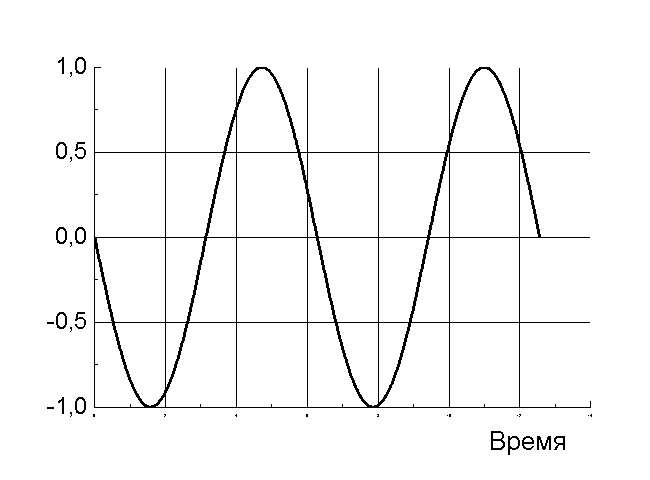
    Б

    В

19. Гармонічне коливання відбувається за законом косинуса із частотою ω₀=1рад/с, початковою фазою φ₀=0 і амплітудою А=1. Укажіть графік залежності прискорення від часу.

А

Б

В

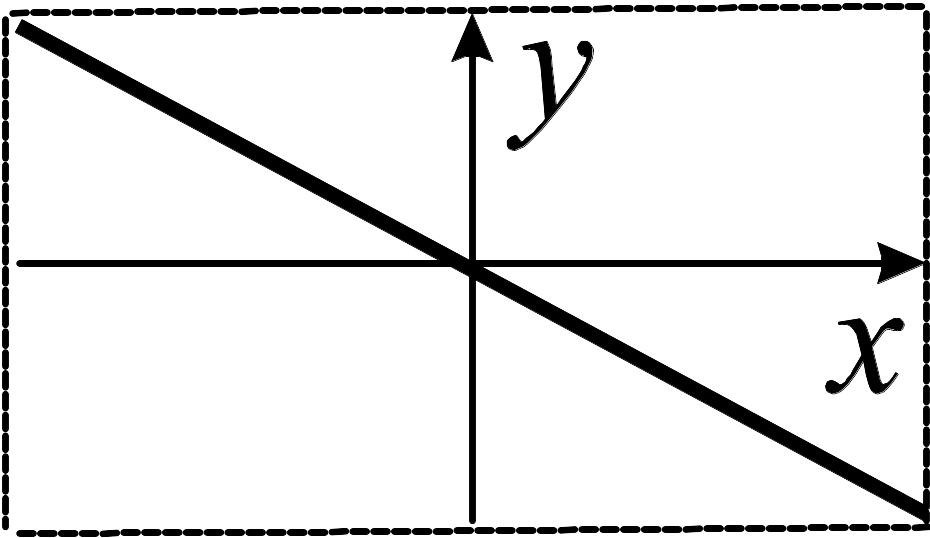
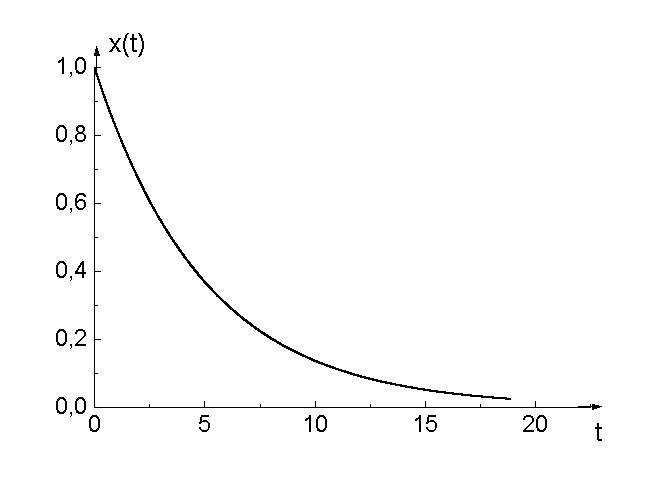
20. Гармонічне коливання відбувається за законом косинуса із частотою ω₀=1рад/с, початковою фазою φ₀=0 і амплітудою А=1. Укажіть графік залежності зсуву від часу.

А

Б

В

.

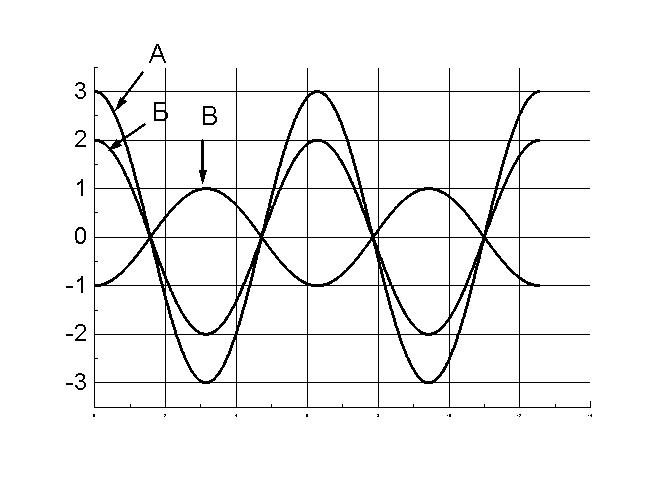
21. Гармонічне коливання відбувається за законом косинуса із частотою ω0=2рад/с, початковою фазою φ0=0 і амплітудою А=1. Укажіть графік залежності швидкості від часу 1. А 2. Б. 3. В
22. Гармонічне коливання відбувається за законом косинуса із частотою ω0=2рад/с, початковою фазою φ0=0 і амплітудою А=1. Укажіть графік залежності зсуву від часу. 1. А 2. Б. 3. В
23. Гармонічне коливання відбувається за законом косинуса із частотою ω0=2рад/с, початковою фазою φ0=0 і амплітудою А=1. Укажіть графік залежності прискорення від часу. 1. А 2. Б. 3. В

24. Вільні гармонічні коливання відбуваються

1. Під дією квазіпружної сили;

2. Під дією зовнішньої періодично діючої сили;

3. Обоє твердження вірні.

24. Між циклічною частотою вільних гармонічних коливань і квазіпружною постійною існує зв'язок:

24. Період вільних гармонічних коливань пружинного маятника пов'язаний із квазіпружною постійною співвідношенням:

24. Фізичним маятником називається

1. Тіло, що виконує коливання в полі тяжіння Землі навколо горизонтальної осі, що не проходить через центр ваги;

2. Тіло, що виконує коливання під дією зовнішньої періодично діючої сили;

3. Матеріальна точка, підвішена на невагомій нерозтяжній нитці й здійснюючого коливання в полі тяжіння Землі.

24. Математичним маятником називається

1. Тіло, що виконує коливання в полі тяжіння Землі навколо горизонтальної осі, що не проходить через центр ваги;

2. Тіло, що виконує коливання під дією зовнішньої періодично діючої сили;

3. Матеріальна точка, підвішена на невагомій нерозтяжній нитці й здійснюючого коливання в полі тяжіння Землі.

24. При відхиленні фізичного маятника на кут φ на нього діє момент сили 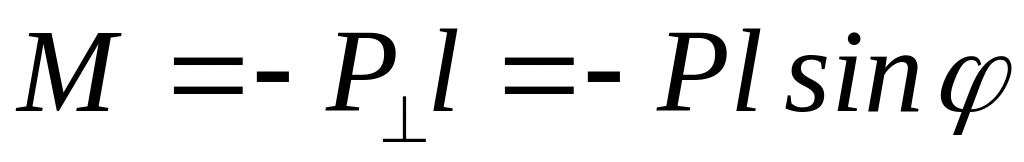, де

1. l – довжина маятника;

2. l – плече сили ваги;

3. l – відстань від центра ваги до осі обертання.

24. Період коливань фізичного маятника визначається формулою:

24. Період коливань математичного маятника визначається формулою:

24. Диференціальне рівняння коливань фізичного маятника має вигляд:

24. Гармонічне коливання відбувається за законом . Тоді потенціальна енергія такого коливання має вигляд:

24. Гармонічне коливання відбувається за законом . Тоді потенціальна енергія такого коливання має вигляд:

35. Гармонічне коливання відбувається за законом . Тоді кінетична енергія такого коливання має вигляд:

36. Гармонічне коливання відбувається за законом . Тоді кінетична енергія такого коливання має вигляд:

37. Повна енергія гармонічного коливання має вигляд:

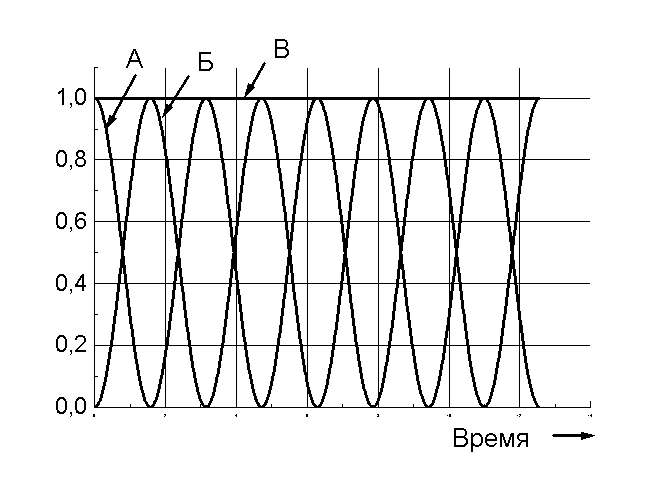
38. Гармонічне коливання відбувається за законом. . Тоді кінетична енергія такого коливання має вигляд, зображений на графіку: 1. А; 2.Б; 3.В

39. Гармонічне коливання відбувається за законом. . Тоді потенціальна енергія такого коливання має вигляд, зображений на графіку: 1. А; 2.Б; 3.В

39. Гармонічне коливання відбувається за законом. . Тоді повна механічна енергія такого коливання має вигляд, зображений на графіку: 1. А; 2.Б; 3.В

40. Гармонічне коливання відбувається за законом. . Тоді кінетична енергія такого коливання має вигляд, зображений на графіку: 1. А; 2.Б; 3.В

.

41. Гармонічне коливання відбувається за законом. . Тоді потенціальна енергія такого коливання має вигляд, зображений на графіку: 1. А; 2.Б; 3.В

42. При додаванні двох скалярних гармонічних коливань однакової частоти результуюча амплітуда коливань знаходиться за формулою:

43. Складаються два гармонічних коливання з однаковою частотою й однаковою фазою. При цьому результуюча амплітуда коливань знаходиться за формулою:

44. Складаються два гармонічних коливання з однаковою частотою й протилежною фазою. При цьому результуюча амплітуда коливань перебуває по формулі:

45. Складаються два гармонічних коливання з однаковою частотою й протилежною фазою. При цьому результуючий зсув має вигляд, зображений на графіку: А; Б; В.

46. Складаються два гармонічних коливання з однаковою частотою й однаковою фазою. При цьому результуючий зсув має вигляд, зображений на графіку: 1. А; 2. Б; 3. В.

47. Необхідними умовами для виникнення биттів є:

1. Амплітуди однакові; частоти однакові; початкові фази однакові;

2.Амплітуди близькі за значенням; частоти однакові; початкові фази однакові;

3.Амплітуди однакові; частоти близькі за значенням; початкові фази однакові.

48. Період биття визначається формулою:

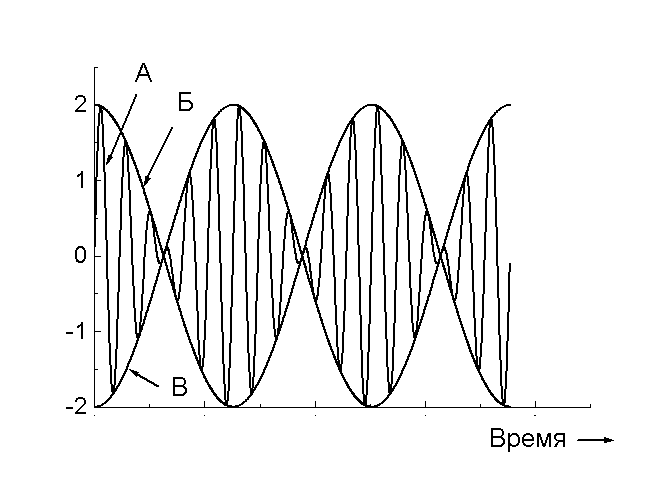
49. Укажіть криву залежності зсуву від часу в процесі биття 1. Б; 2. А; 3. В.

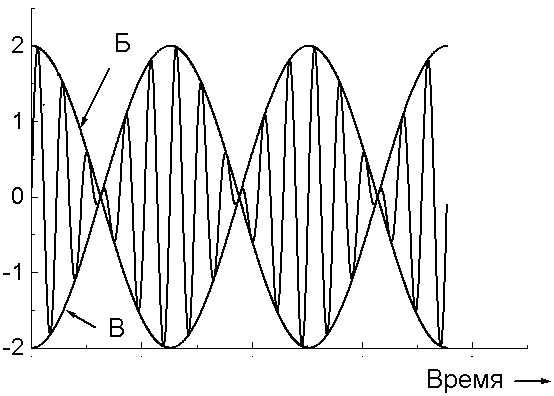
50. Укажіть криву залежності амплітуди від часу в процесі биття 1. Б; 2. В; 3. Обидві відповіді вірні.

51. Складаються два взаємно перпендикулярних гармонічних коливання з однаковою частотою. При цьому результуючий рух описується рівнянням:

52. При додаванні двох взаємно перпендикулярних гармонічних коливань із однаковою частотою результуючий рух описується рівнянням:

При цьому зсув x змінюється в межах:

1. Від 0 до А₁; 2. від – А₁ до + А₁; 3. від – ( А₁+А₂)/2 до +( А₁+А₂)/2.

53. При додаванні двох взаємно перпендикулярних гармонічних коливань із однаковою частотою результуючий рух описується рівнянням:

При цьому зсув у змінюється в межах:

1. Від 0 до А₂; 2. від – А₂ до + А₂; 3. від – ( А₁+А₂)/2 до +( А₁+А₂)/2.

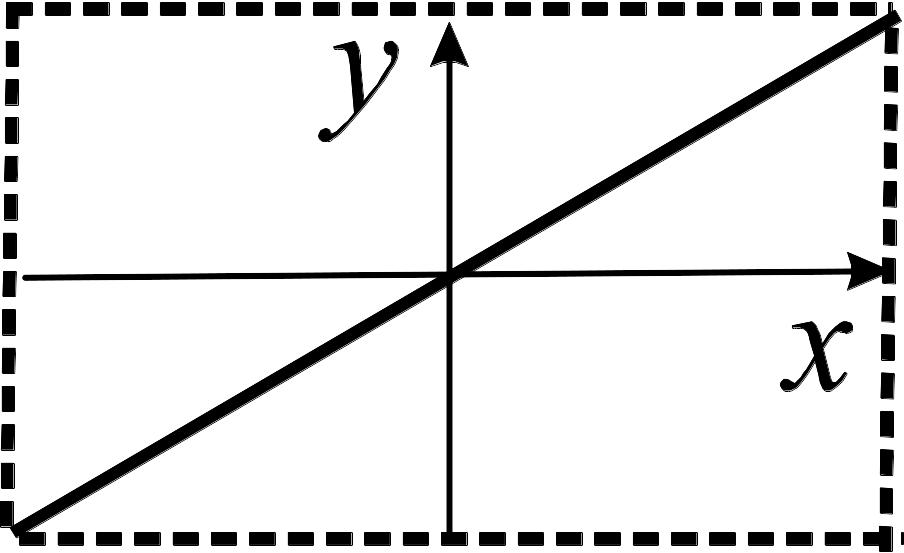
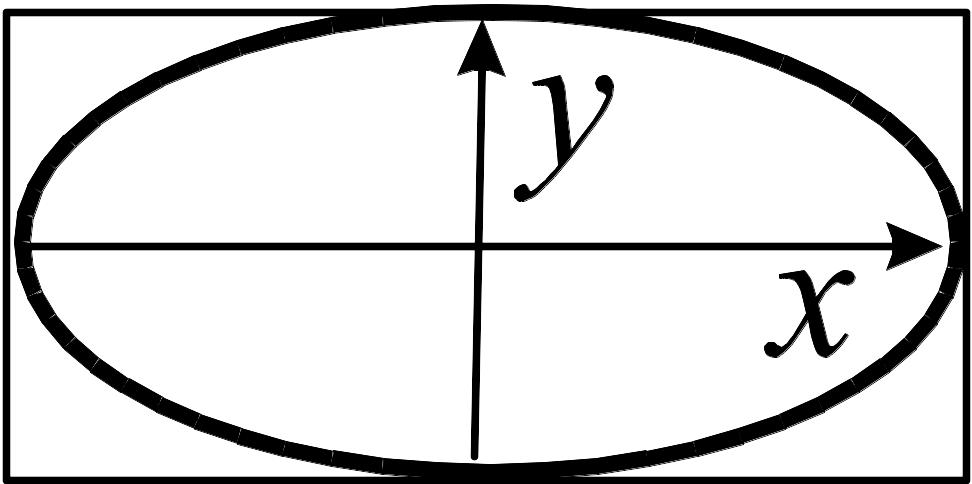
54. Укажіть умови, при яких виходить фігура Ліссажу, показана на рисунку: 1. Частоти коливань, що складаються, рівні; початкові фази збігаються. 2. Частоти коливань, що складаються, рівні; початкові фази протилежні. 3. Частоти коливань, що складаються, рівні; початкові фази відрізняються на π/2.
55. Укажіть умови, при яких виникає фігура Ліссажу, показана на рисунку: 1. Частоти коливань, що складаються, рівні; початкові фази збігаються. 2. Частоти коливань, що складаються, рівні; початкові фази протилежні. 3. Частоти коливань, що складаються, рівні; початкові фази відрізняються на π /2.

56. Укажіть умови, при яких виходить фігура Ліссажу, показана на рисунку: 1. Частоти коливань, що складаються, рівні; початкові фази збігаються. 2. Частоти коливань, що складаються, рівні; початкові фази протилежні. 3. Частоти коливань, що складаються, рівні; початкові фази відрізняються на π /2.

57. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямій, що проходить через перший і третій квадранти;

2. прямій, що проходить через другий і четвертий квадранти;

3. кола.

58. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямій, що проходить через перший і третій квадранти;

2. прямій, що проходить через другий і четвертий квадранти;

3. кола.

59. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямої, що проходить через перший і третій квадранти;

2. прямої, що проходить через другий і четвертий квадранти;

3. кола.

60. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямої, що проходить через перший і третій квадранти;

2. прямої, що проходить через другий і четвертий квадранти;

3. еліпса.

61. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямої, що проходить через перший і третій квадранти;

2. прямої, що проходить через другий і четвертий квадранти;

3. еліпса.

62. Складаються два взаємно перпендикулярних коливання . При цьому фігура Ліссажу буде мати вигляд

1. прямої, що проходить через перший і третій квадранти;

2. прямої, що проходить через другий і четвертий квадранти;

3. еліпса.

63. Загасаючі коливання відбуваються під дією

1. сили опору

2. квазіпружної сили

3. спільної дії квазіпружної сили й сили опору

64. Загасаючі коливання відбуваються за законом , де

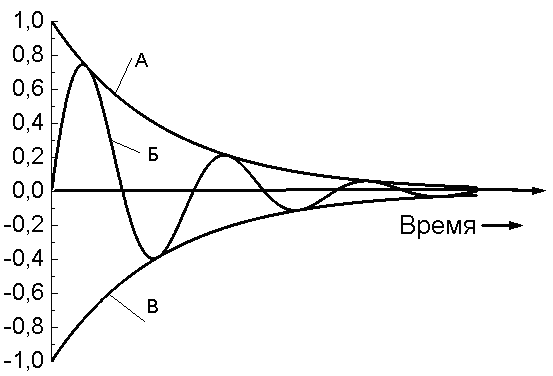
65. На рисунку наведений графік загасаючих коливань. Укажіть, яка із кривих відповідає зсуву, амплітуді:

Зсув Амплітуда 1. Б А 2. А Б 3. В А

66. Амплітуда загасаючих коливань змінюється за законом:

67. Логарифмічний декремент загасання дорівнює

1. частоті загасаючих коливань;

2. періоду загасаючих коливань;

3. логарифму відношенню амплітуд, узятих через проміжок часу, рівному періоду коливань.

68. Логарифмічний коефіцієнт загасання пов'язаний з періодом коливань Т і коефіцієнтом загасання β співвідношенням:

69. На рисунку показана залежність амплітуди коливань від часу для трьох загасаючих коливань із різними коефіцієнтами загасання β₁, β₂, β_3. Укажіть правильне співвідношення між цими значеннями.

β1< β2< β3; β1> β2< β3; β1> β2> β3.

70. На рисунку показана залежність амплітуди коливань від часу для трьох загасаючих коливань із різними значеннями логарифмічного декремента загасання λ₁, λ ₂, λ _3. Укажіть правильне співвідношення між цими значеннями.

λ 1< λ 2< λ 3; λ 1> λ 2< λ 3; λ 1> λ 2> λ 3.

71. На рисунку показаний графік залежності зсуву від часу для системи, що виконує загасаючі коливання. Це 1. випадок аперіодичного руху, коли сила опору перевищує квазіпружну силу. 2. випадок аперіодичного руху, коли . 3. випадок аперіодичного руху, коли .

72. Добротність системи визначає втрати механічної енергії на подолання сил опору за час, рівний періоду коливань. При цьому

1. Чим вище добротність, тим менше втрати;

2. Чим вище добротність, тим більше втрати.

3. Обидві відповіді неправильні.

73. Добротність системи можна визначити по формулі:

1. , де – втрати механічної енергії на подолання сил опору за час, рівний періоду коливань

2. , де λ - логарифмічний декремент загасання.