5.Основні визначення статистики Максвелла
Розподіл Максвелла - це розподіл часток по
1) потенціальним енергіям;
2) швидкостям;
3) повній механічній енергії.
Функція розподілу Максвелла визначає
1) абсолютне число часток, що
мають швидкості в інтервалі від
до
;
2)
абсолютне число часток, що мають енергії
в інтервалі від
до
;
3) відносне число часток, що мають швидкості в інтервалі від до .
Функція розподілу Максвелла визначає
1) абсолютне число часток, що мають швидкості в інтервалі від до ;
2) відносне число часток, що мають швидкості в інтервалі від до ;
3) відносне число часток, що мають швидкості в одиничному інтервалі.
Функція розподілу Максвелла визначає
1) абсолютне число часток, що мають швидкість ;
2) відносне число часток, що мають швидкість ;
3) відносне число часток, що мають швидкість в інтервалі від до .
Функція розподілу Максвелла визначає
1) абсолютне число часток, що мають швидкості в інтервалі від до ;
2) число часток в одиничному об’ємі, що має швидкості в інтервалі від до ;
3) відносне число часток, що мають швидкості в інтервалі від до .
Функція розподілу Максвелла визначається виразом
1)
; 2)
; 3)
.
При даній температурі найбільше число молекул мають швидкість поблизу
1) середньої швидкості;
2) середньоквадратичної швидкості;
3) найбільш імовірної швидкості.
Найбільш імовірна швидкість молекул це
1) середнє значення всіх швидкостей молекул;
2) середнє значення модулів всіх швидкостей молекул;
3) швидкість, близьку до якої має максимальна кількість молекул.
Середньоквадратична швидкість це
1) квадрат від середньої швидкості молекул;
2) корінь квадратний від середнього квадрата швидкостей молекул;
3) найбільш імовірна швидкість у квадраті.
Середня швидкість молекул це
1) швидкість, що мають більшість молекул;
2) середнє значення модулів швидкостей всіх молекул;
3) обоє твердження вірні.
Середньоквадратична швидкість молекул газу при даному тиску залежить від
1) температури;
2) об’єму;
3) обидва твердження вірні.
У даному об’ємі при даній температурі Т швидкості молекул
1) однакові;
2) лежать в інтервалі
;
3) можуть бути будь-якими.
Середньоквадратична швидкість молекул кисню на рівні моря була 500 м/с. Який стала середньоквадратична швидкість на висоті 5 км? (Уважати температуру постійною).
1) 372 м/с 2) 500 м/с; 3) 813 м/с.
Графік функції розподілу Максвелла зображений на рисунку
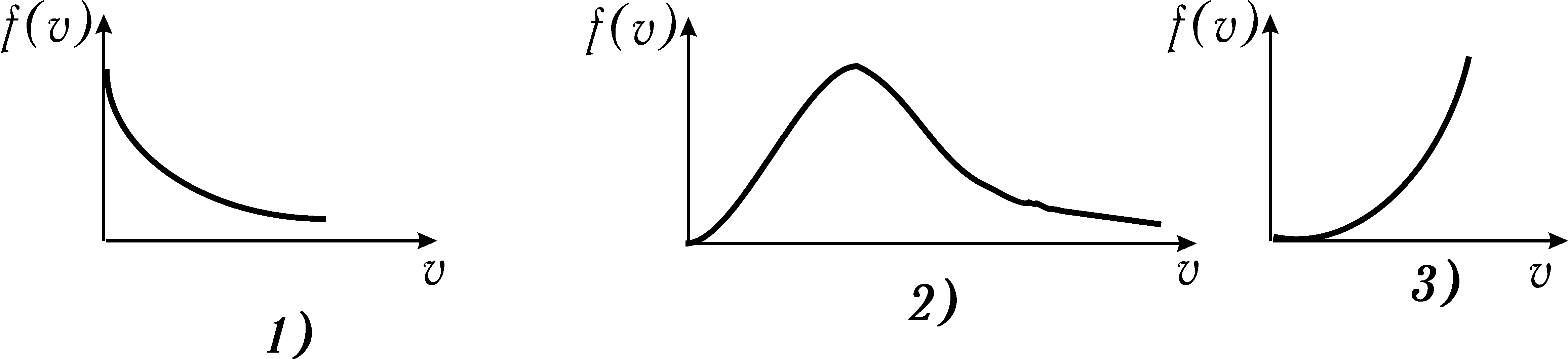
Функція розподілу Максвелла для двох температур зазначена правильно на рисунку
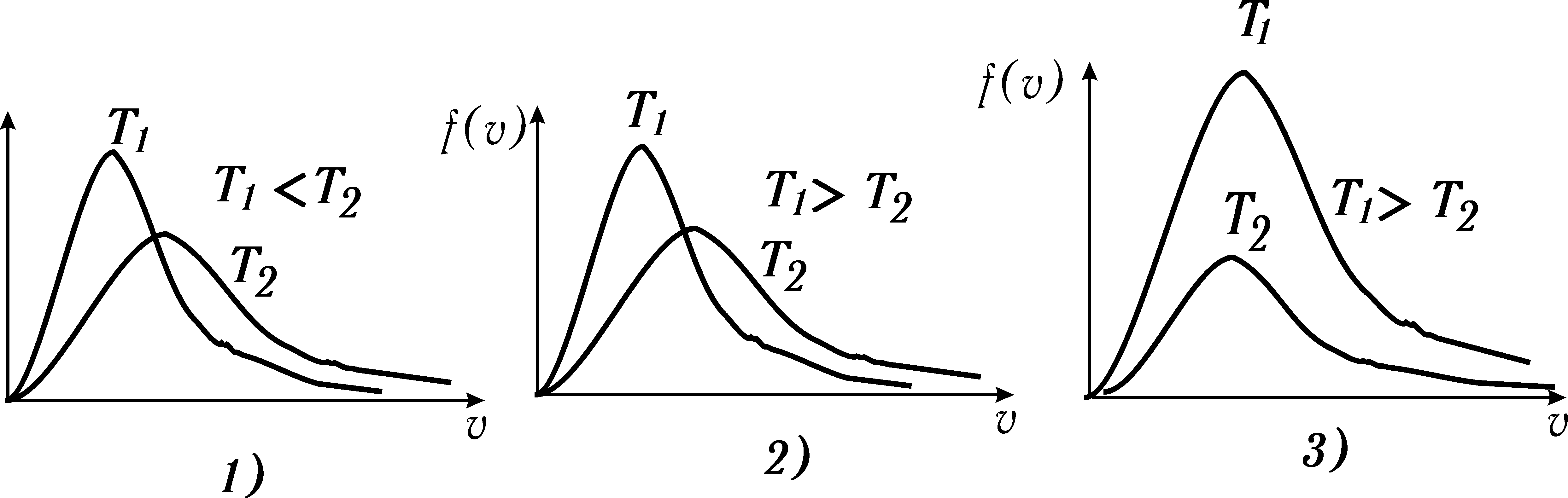
Н
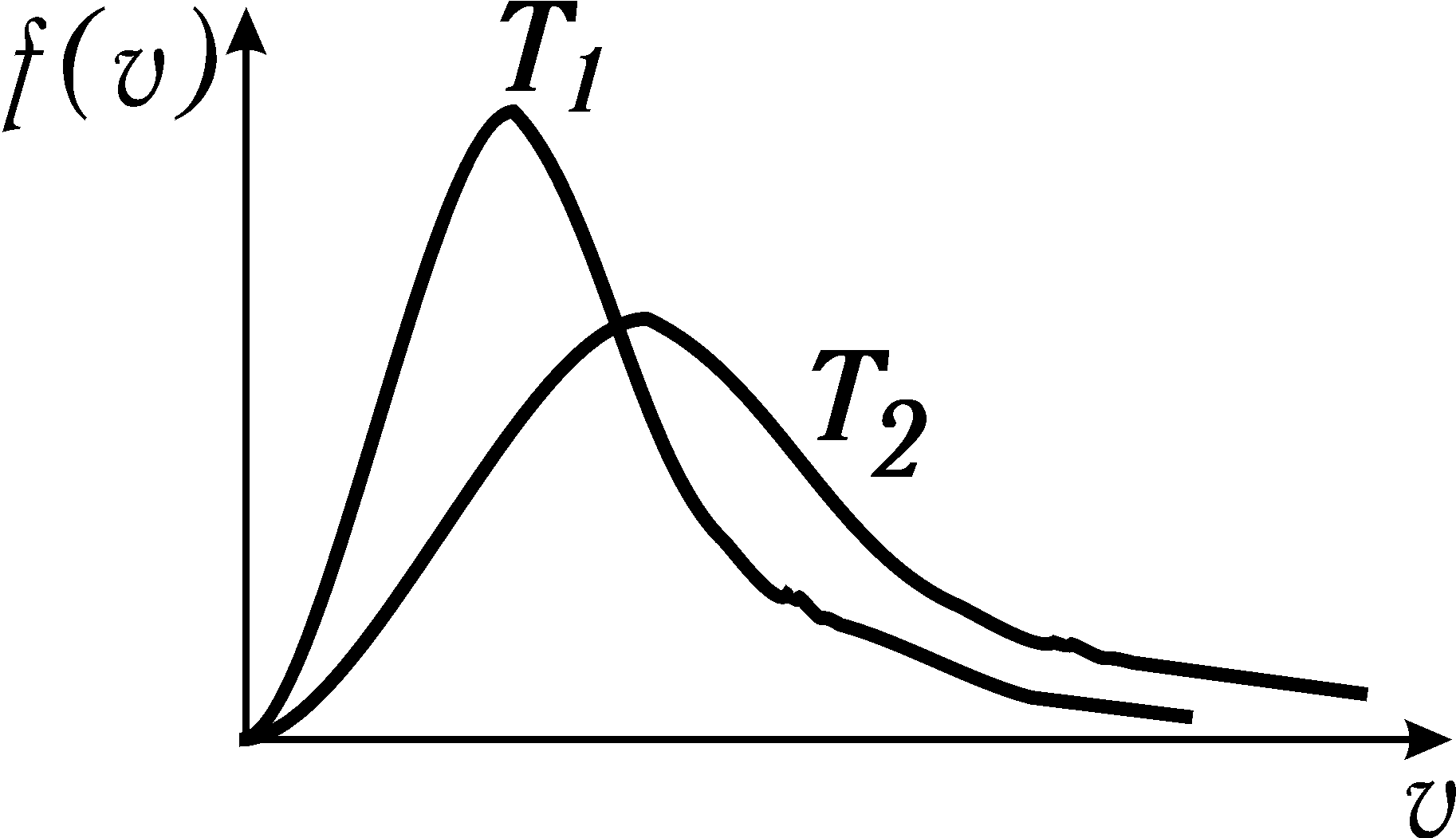а
рисунку показані криві розподілу
Максвелла при двох температурах. Як
співвідносяться температури?
а)
;
б)
;
в)
.
Площа заштрихованої фігури на графіку
визначає
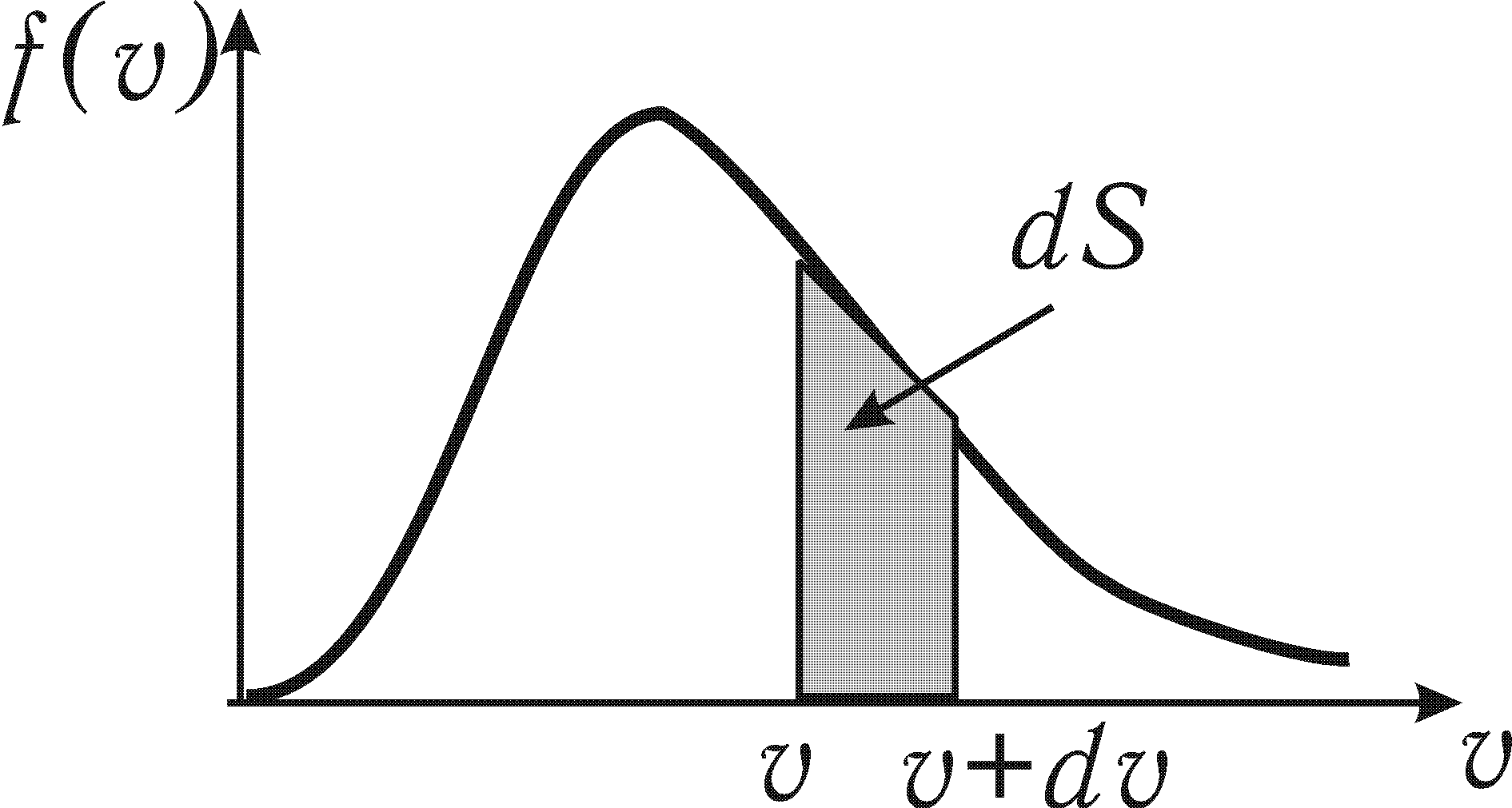
1) абсолютне число часток, що мають швидкості в інтервалі від до ;
2) число часток в одиничному об’ємі, що має швидкості в інтервалі від до ;
3) відносне число часток, що мають швидкості в інтервалі від до .
Умова нормування функції розподілу Максвелла виглядає як
1)
; 2)
; 3)
.
Площа під кривою від функції розподілу Максвелла дорівнює
1) одиниці;
2) числу молекул газу;
3) числу молекул в одиниці об'єму газу.
При збільшенні температури площа під кривою функції розподілу Максвелла
1) збільшується;
2) зменшується;
3) залишається постійною.
Найбільш імовірна швидкість знаходиться по формулі
1)
; 2)
; 3)
.
Середня швидкість молекул газу знаходиться по формулі
1) ; 2) ; 3) .