- •1. Основні положення мкт. Ідеальний газ.
- •Основні визначення (тиск, густина, кількість речовини, константи й розмірність)
- •2) Число молекул у речовини;
- •3) Число молекул у речовини;
- •Кількість речовини можна знайти по формулі
- •2. Основне рівняння мкт, температура, середньоквадратична швидкість
- •Основне рівняння молекулярно-кінетичної теорії записується так:
- •Основне рівняння молекулярно-кінетичної теорії записується так:
- •Основне рівняння молекулярно-кінетичної теорії записується так:
- •Температура знизилася з до . Як змінилася при цьому середньоквадратична швидкість молекул?
- •1) Зменшилася в 2 рази;
- •3. Рівняння Менделеева-Клапейрона, газові закони
- •Рівняння Менделеева-Клапейрона має вигляд
- •Рівняння Менделеева-Клапейрона має вигляд
- •Рівняння ізобари має вигляд
- •4. Складні завдання на газові закони
- •5.Основні визначення статистики Максвелла
- •6. Знання формул для статистики Максвелла, середньоквадратична швидкість
- •7.Розподіл Больцмана (не скрізь знання формули)
- •1) ; 2) ; 3) Обидві формули вірні.
- •8. Довжина вільного пробігу молекули
- •9. Термодинаміка. Визначення. 1-е начало. Прості питання.
- •10.Перше начало термодинаміки для ізопроцесів. Складні формули. Задачі.
- •11.Теплоємність, адіабатний процес
- •12. Теплові машини
- •13. Друге начало термодинаміки. Ентропія
- •3. Обидві формули вірні.
- •3. Обидві формули вірні.
3. Обидві формули вірні.
93. Гучність звуку визначається
1. інтенсивністю (силою) звуку;
2. частотою;
3. формою звукових коливань.
94. Висота звуку визначається
1. інтенсивністю (силою) звуку;
2. частотою;
3. формою звукових коливань.
95. Тембр звуку визначається
1. інтенсивністю (силою) звуку;
2. частотою;
3. формою звукових коливань.
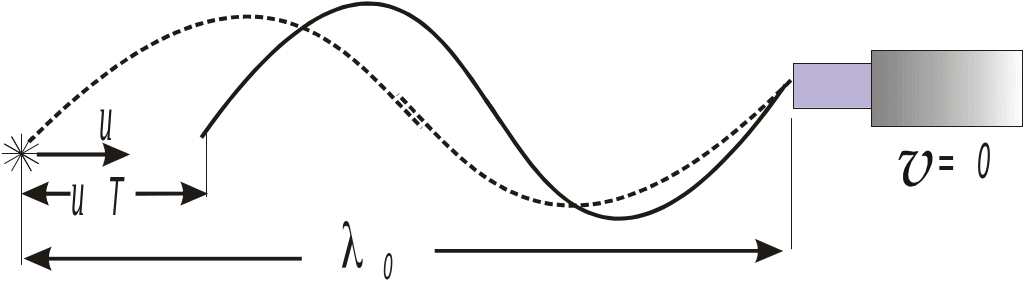
96. На рисунку показаний випадок руху приймача назустріч джерела звуку. При цьому приймач реєструє частоту:
|
|
1.
|
|
97. На рисунку показаний випадок, коли приймач віддаляється від джерела звуку. При цьому приймач реєструє частоту:
|
|
1. ; 2. ; 3. |
|
98. На рисунку показаний випадок, коли джерело звуку наближається до приймача. При цьому приймач реєструє частоту:
|
|
1.
|
|
99. На рисунку показаний випадок, коли джерело звуку віддаляється від приймача. При цьому приймач реєструє частоту:
|
|
1. ; 2. ; 3. |
|
Задачі
100. Амплітуда вимушених коливань залежить від частоти зовнішньої періодично діючої сили ω по формулі:

Виходячи із цієї формули, покажіть, що резонансна частота визначається виразом:
.![]()
101. Гармонічне коливання
відбувається за законом
![]() .
Чому дорівнює швидкість у момент часу
t=0?
.
Чому дорівнює швидкість у момент часу
t=0?
1).
![]() ;
2). 3/2;
3). 2.
;
2). 3/2;
3). 2.
102. Гармонічне коливання
відбувається за законом
![]() .
Чому дорівнює швидкість у момент часу
t=0?
.
Чому дорівнює швидкість у момент часу
t=0?
1).
;
2). –![]() ;
3). 2.
;
3). 2.
103. Гармонічне коливання відбувається за законом . Чому дорівнює прискорення в момент часу t=0?
1).
![]() ;
2). 3/2; 3).
;
2). 3/2; 3).
![]() .
.
104. Гармонічне коливання
відбувається за законом
![]() .
Чому дорівнює період коливань?
.
Чому дорівнює період коливань?
1).
![]() ;
2).
;
2).
![]() ;
3). 2.
;
3). 2.
105. Гармонічне коливання
відбувається за законом
![]() .
Чому дорівнює період коливань?
.
Чому дорівнює період коливань?
1).
![]() ;
2).
;
2).
![]() ;
3). 1.
;
3). 1.
106. Пружинний маятник масою m=100 м виконує гармонічні коливання із частотою ω0 = 30 рад/с. Чому дорівнює жорсткість пружини?
1.90 Н/м; 2.30 Н/м; 3.45 Н/м.
107. На пружині жорсткістю до= 1 кН/м укріплений вантаж масою m= 1 кг. Чому дорівнює період коливань такого пружинного маятника?
1.6.28 з; 2.1 з; 3.3.14 с.
108. Визначити силу
F, що повертає,
у момент часу t=1/8 c
точки
масою m=20 г,
що виконує
гармонічні коливання відповідно до
рівняння
![]() ,
де А=15 см,
,
де А=15 см,
ω=4 с-1.
1. -1.43 Н; 2.1.43 Н; 3.0.
109. Визначити потенціальну енергію Wp у момент часу t=1/8 c точки масою m=20 г, що виконує гармонічні коливання відповідно до рівняння , де А=15 см, ω=4 с-1.
1.0. 214 Дж; 2.0. 107 Дж. 3. 0.
110. Визначити кінетичну енергію Wк у момент часу t=1/8 c точки масою m=20г, що виконує гармонічні коливання відповідно до рівняння , де А=15 см, ω=4 с-1.
1. 0. 214 Дж; 2. 0. 107 Дж. 3. 0.
111. Визначити повну енергію точки масою m=20 г, що виконує гармонічні коливання відповідно до рівняння , де А=20 см, ω=4 с-1.
1.3.14·10 -2 Дж; 2.6.31·102 Дж; 3.5.14·102 Дж;
112. Визначити
максимальну швидкість
![]() матеріальної точки,
що виконує
гармонічні коливання відповідно до
рівняння
,
де А= 2 см,
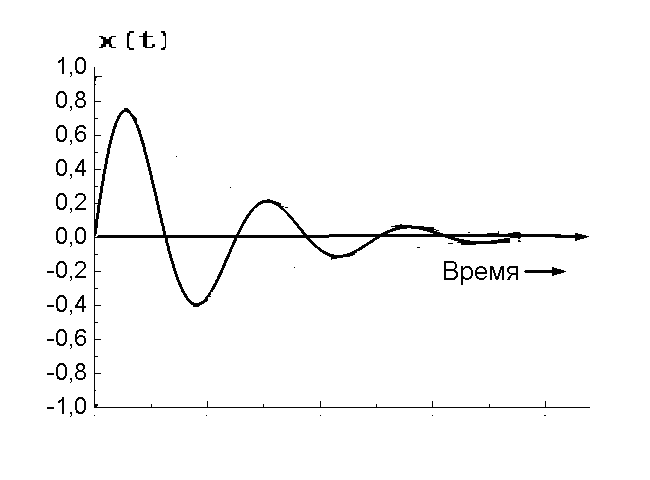
ω= 3 с-1.
матеріальної точки,
що виконує
гармонічні коливання відповідно до
рівняння
,
де А= 2 см,
ω= 3 с-1.
1.6·10 -2 м/с; 2.3·10 -2 м/с; 3.1. 5·10 -2 м/с.
113. Визначити
максимальне
по модулю
прискорення
![]() матеріальної точки,
що виконує
гармонічні коливання відповідно до
рівняння
,
де А= 2 см,
ω= 3 с-1.
матеріальної точки,
що виконує
гармонічні коливання відповідно до
рівняння
,
де А= 2 см,
ω= 3 с-1.
1.0.18 м/с2; 2.0.36 м/с2; 3.0.72 м/с2 .
114. Матеріальна точка виконує гармонічні коливання відповідно до рівняння , де ω=2 с-1. У який момент часу зсув дорівнює половині амплітуди?
1.0.13 с. 2.0.52 с. 3.0.26 с.
115. Матеріальна точка
виконує
гармонічні коливання відповідно до
рівняння
,
де ω=2 с-1.
У який момент часу зсув
дорівнює
![]() значення амплітуди?
значення амплітуди?
1.0.13 с. 2.0.52 с. 3.0.26 с.
116. На пружині жорсткістю к= 4 кН/м укріплений вантаж масою m= 1 кг. Напишіть рівняння коливань такого пружинного маятника, якщо амплітуда коливань А= 2 см.
1). x=0.02 cos2t; 2) x=0.02 cos4t; 3) x=0.02 cost.
117. Матеріальна точка
виконує
гармонічні коливання відповідно до
рівняння
,
де ω=2 с-1.
У який момент часу зсув
дорівнює
![]() значення амплітуди?
значення амплітуди?
1.0.13 с. 2.0.52 с. 3.0.39 с.
118. Матеріальна точка виконує гармонічні коливання з періодом Т=4 с. У деякий момент часу зсув максимальний. Через який проміжок часу Δt швидкість досягне максимального значення?
1) 1 c; 2) 2 c; 3) 4 с.
119. Матеріальна точка виконує гармонічні коливання з періодом Т=4 с. У деякий момент часу швидкість максимальна. Через який проміжок часу Δt прискорення досягне максимального значення?
1) 1 c; 2) 2 c; 3) 4 с.
120. Матеріальна точка виконує гармонічні коливання з періодом Т=4 с. У деякий момент часу прискорення максимально. Через який проміжок часу Δt швидкість досягне максимального значення?
1) 1 c; 2) 2 c; 3) 4 с.
121. Матеріальна точка виконує гармонічні коливання з амплітудою А. При яких значеннях зсуву х швидкість максимальна?
1) х = 0; 2) х = А; 3) х = А/2.
122. Матеріальна точка виконує гармонічні коливання з амплітудою А. При яких значеннях зсуву х прискорення максимально?
1) х = 0; 2) х = А; 3) х = А/2.
123. Матеріальна точка виконує гармонічні коливання з амплітудою А. При яких значеннях зсуву х прискорення й швидкість одночасно досягають максимального значення?
1) х = 0; 2) х = А; 3) Такий стан не реалізується.
124. Матеріальна точка виконує гармонічні коливання з періодом Т=4 с.. У деякий момент часу кінетична енергія максимальна. Через який проміжок часу потенціальна енергія досягне максимального значення?
1) 2 c; 2) 1 c; 3) 4 с.
125. Знайти максимальну
кінетичну енергію матеріальної точки
масою m=2 г,
що виконує
гармонічні коливання з
амплітудою А= 4 см
і частотою
![]() .
.
1) 0.04 мДж; 2) 3.16 мДж; 3) 1.58 мДж.
126. Точка виконує гармонічні коливання. У деякий момент часу зсув точки x=5 см і модуль прискорення │a│= 80 см/с2. Знайти циклічну частоту коливань ω.
1) 4 с-1; 2) 16 с-1; 3) 8 с-1.
127. Точка
виконує
гармонічні коливання c частотою ω =
10 с-1.
У деякий момент часу зсув точки
x=4 см
і модуль швидкості │v│=
30 см/с.
Знайти амплітуду
коливань. Вказівка:
скористайтеся
тотожністю
![]() .
.
1) 3 см; 2) 5 см; 3) 4 см.
128. Матеріальна точка масою m= 100 г виконує гармонічні коливання, рівняння яких має вигляд x=A·sinωt, де А=5 см, ω =2с-1. У який момент часу (найближчий до початку відліку) сила, що повертає, F= -10-2 Н?
1) π/3; 2) π/6; 3) π/12.
129. Два гармонічних коливання, спрямованих уздовж одній прямій, що мають однакові амплітуди й періоди, складаються в одне коливання тієї ж амплітуди. Знайти різницю фаз коливань, що складаються.
1) 600; 2) 900; 3) 1200.
130. Точка
виконує
одночасно два
гармонічних коливання, що відбуваються
у взаємно перпендикулярним напрямкам
і описуються рівняннями:
![]() і
і
![]() ,
де А1=
4 см,
ω1 =
π с-1;
А2= 8
см,
ω2=π
с-1,
τ=1 с. Знайти рівняння траєкторії.
,
де А1=
4 см,
ω1 =
π с-1;
А2= 8
см,
ω2=π
с-1,
τ=1 с. Знайти рівняння траєкторії.
1.
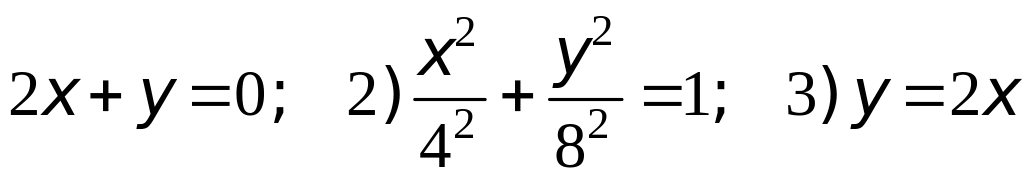 .
.
131. Точка
виконує
одночасно два
гармонічних коливання, що відбуваються
уздовж однією
прямою й описуються рівняннями:
![]() і
і
![]() ,
де А1=
4 см,
А2 =
8 см,
ω = π с-1,
τ = 1 с. Знайти результуючу амплітуду
коливань.
,
де А1=
4 см,
А2 =
8 см,
ω = π с-1,
τ = 1 с. Знайти результуючу амплітуду
коливань.
1) 6 см;
2) 4 см;
3)
![]() см.
см.
132. Точка виконує одночасно два гармонічних коливання, що відбуваються уздовж однією прямою й описуються рівняннями: і , де А1= 4 см, А2=3 см, ω=π с-1, τ=0.5 с. Знайти результуючу амплітуду коливань
1) 1 см; 2) 7 см; 3) 5 см.
133. Точка виконує одночасно два гармонічних коливання, що відбуваються уздовж однією прямою й описуються рівняннями: і , де А1= 4 см, А2=3 см, ω=π с-1, τ =1/3 с. Знайти результуючу амплітуду коливань
1) 31 см; 2) 7 см; 3) 1 см.
134. Точка виконує одночасно два гармонічних коливання, що відбуваються уздовж однією прямою й описуються рівняннями: і , де А1= 4 см, А2=3 см, ω=π с-1, τ =1/6 с. Знайти результуючу амплітуду коливань
1) 5 см; 2) 5.9 см; 3) 7 см.
135. Точка виконує одночасно два гармонічних коливання, що відбуваються у взаємно перпендикулярним напрямкам і описуються рівнянням: і , де А1= 4 см, ω1 = π с-1; А2= 8 см, ω2=π с-1, τ=0. Знайти рівняння траєкторії.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
136. Точка виконує одночасно два гармонічних коливання, що відбуваються у взаємно перпендикулярним напрямкам і описуються рівнянням: і , де А1= 4 см, ω1 = π с-1; А2= 8 см, ω2=π с-1, τ = 0.5 с. Знайти рівняння траєкторії.
1) .
137. Точка
виконує
одночасно два
гармонічних коливання, що відбуваються
у взаємно перпендикулярним напрямкам
і описуються рівнянням:
![]() .
Знайти траєкторію руху
точки.
.
Знайти траєкторію руху
точки.
 .
.
138. Знайти лінійну частоту коливань вантажу масою 400 г, підвішеного до пружини жорсткістю 160 Н/м.
1) 3.2 Гц; 2) 20 Гц; 3) 400 Гц.
139. Знайти масу вантажу, що на пружині із жорсткістю 250 Н/м виконує 20 коливань за 16 с.
1) 3 кг; 2) 4 кг; 3) 5 кг.
140. У скільки разів зміниться частота коливань автомобіля на ресорах після прийняття вантажу, рівного масі порожнього автомобіля?
1) збільшиться в
![]() разу; 2) не зміниться; 3)
зменшиться в
разу.
разу; 2) не зміниться; 3)
зменшиться в
разу.
141. Кулька, підвішена на тонкій нерозтяжній нитці, виконує коливання з періодом Т. У скільки разів зміниться період коливань тієї ж кульки, якщо відрізати 3/4 довжини нитки й підвісити ту частину, що залишилася.
1) збільшиться в 2 рази; 2) не зміниться; 3) зменшиться в 2 рази.
142. Вантаж масою 1
кг, підвішений
до пружини із жорсткістю
100Н/м,
виконує
коливання з
амплітудою 10 см.
Написати рівняння
![]() руху
вантажу.
руху
вантажу.
1)
![]()
143. Чому дорівнює прискорення вільного падіння, якщо математичний маятник довжиною 80 см виконав за 3 хв 100 коливань?
1) 9.81 м/с2; 2) 9.74 м/с2; 3) 9.78 м/с2.
144. Як відносяться довжини математичних маятників, якщо за один і той же час один з них виконує 10, а другий 30 коливань?
1) 3:1; 2) 1:3; 3) 9:1.
145. За один і той же час один математичний маятник виконує 50 коливань, а другий 30. Знайти їхні довжини, якщо один з них на 32 см коротше іншого.
1) l1=50 cм, l2 =18 cм; 2) l1=60 cм, l2 =28 cм; 3 l1=40 cм, l2 =8 cм.
146. Вантаж виконує коливання на пружині жорсткістю k = 250 Н/м. Амплітуда коливань A = 15 см. Знайти повну механічну енергію коливань.
1) 1.4 Дж; 2) 2.8 Дж; 3) 4.2 Дж.
147. У скільки разів змінилася повна механічна енергія математичного маятника при зменшенні довжини в 3 рази й збільшенні амплітуди в 2 рази?
1) збільшилася в 12 разів; 2) зменшилася в 12 разів; збільшилася в 6 разів.
148. Вантаж, підвішений на пружині із жорсткістю k = 1кН/м, коливається з амплітудою A=2 см. Знайти кінетичну Wk і потенціальну Wp енергію при фазі π/3 рад. Вказівка: для однозначності відповіді виразіть рівняння руху через косинус.
1) Wk=50 мДж , Wp=150 мДж ;
2) Wk=150 мДж , Wp=50 мДж ;
3) Wk=120мДж , Wp=80 мДж ;
149. Пружинний маятник вивели з положення рівноваги й відпустили. Через який час (у частках періоду) кінетична енергія коливного тіла буде дорівнює потенціальній енергії пружини?
1) Т/2; 2) Т/4; 3) Т/8.
150. Частка масою m = 0.01 кг виконує гармонічні коливання з періодом Т = 2 с. Повна енергія коливної частки W=0.1 мДж. Визначити амплітуду А коливань.
1) 45 мм; 2) 54 мм; 3) 24 мм.
151. Матеріальна точка
бере участь одночасно у двох
взаємно перпендикулярних гармонічних
коливаннях, рівняння яких:
![]() ,
де А1=1
см,
ω1=π
с-1;
А2=2
см,
ω1=π/2
с-1.
Знайти рівняння
траєкторії точки.
,
де А1=1
см,
ω1=π
с-1;
А2=2
см,
ω1=π/2
с-1.
Знайти рівняння
траєкторії точки.
1)
![]() 2)
2)
![]() 3)
3)
![]()
152. Визначити
частоту
![]() гармонічних коливань диска радіусом
R=20 см
навколо
горизонтальної осі, що проходить через
середину радіуса диска перпендикулярно
його площині.
Довідка: власний момент диска
гармонічних коливань диска радіусом
R=20 см
навколо
горизонтальної осі, що проходить через
середину радіуса диска перпендикулярно
його площині.
Довідка: власний момент диска
![]() .
.
1) 0.76 Гц; 2) 0.98 Гц; 3) 0.67 Гц.
153. Визначити частоту гармонічних коливань диска радіусом R =20 см навколо горизонтальної осі, що проходить через обід диска перпендикулярно його площині. Довідка: власний момент диска .
1) 0.51 Гц; 2) 0.61 Гц; 3) 0.71 Гц;
154. Визначити
частоту
гармонічних коливань стрижня довжиною
l=20
см навколо
горизонтальної осі, що відстоїть від
середини стрижня на відстані l/4
і
розташованої
перпендикулярно його площині.
Довідка: власний момент стрижня
![]() .
.
1) 1.46 Гц; 2) 3.86 Гц; 3) 2.26 Гц.
155. Визначити частоту гармонічних коливань стрижня довжиною l=20 см навколо горизонтальної осі, що проходить через кінець стрижня перпендикулярно його площині. Довідка: власний момент стрижня .
1) 1.56 Гц; 2) 1.46 Гц; 3) 1.36 Гц.
156. Визначити
частоту
гармонічних коливань кулі
радіусом R=20 см
навколо
горизонтальної осі, що відстоїть від
центра
кулі
на відстані 2R.
Довідка: власний момент кулі
![]() .
.
1) 0.92 Гц; 2) 0.62 Гц; 3) 0.32 Гц.
157. Через час, рівний періоду коливань Т = 2 с, амплітуда загасаючих коливань зменшилася в 2 рази. Визначити логарифмічний декремент загасання λ і коефіцієнт загасання β.
1) λ= 0.301, β=0.15 з-1; 2) λ= 0.693, β=0.346 з-1; 3) λ= 1, β=0.5 з-1.
158. Амплітуда загасаючих
коливань убуває за законом
![]() .
Частота коливань
=2
Гц. Визначити
логарифмічний
декремент
загасання λ.
.
Частота коливань
=2
Гц. Визначити
логарифмічний
декремент
загасання λ.
1) 0.25; 2) 0.5; 3) 0.75.
159. Амплітуда загасаючих коливань убуває за законом . Частота коливань =2 Гц. Визначити логарифмічний декремент загасання λ і добротність Q.
1) λ =0.5, Q=6.28; 2) λ =0.25, Q=12.56 ; 3) λ =0.75, Q=4.19.
160. Загасаючі коливання
описуються рівнянням
![]() ,
де β=2 з-1,
ω=12 с-1.
Визначити
логарифмічний
декремент
загасання λ
і добротність Q.
,
де β=2 з-1,
ω=12 с-1.
Визначити
логарифмічний
декремент
загасання λ
і добротність Q.
1) λ =0.5, Q=6.28; 2) λ =1.05, Q=3; 3) λ =0.75, Q=4.19.
161. Загасаючі коливання описуються рівнянням , де β=2 з-1, ω=10 с-1. Визначити логарифмічний декремент загасання λ і добротність Q.
1) λ =0.5, Q=6.28; 2) λ =0.17, Q=18.5; 3) λ =1.26, Q=2.5.
162. У деякий момент часу повна механічна енергія системи, що виконує загасаючі коливання, була W1= 2 мДж. Через час, рівний періоду коливань, енергія системи стала рівної W2= 1.95 мДж. Визначити добротність системи Q і логарифмічний коефіцієнт загасання λ.
1) Q =40 , λ =7.85· 10-2 ; 2) Q =50 , λ = 6.28· 10-2; 3) Q =80 , λ =3.92 · 10-2 .
163. Усередині системи масою
m=1 кг,
що виконує
загасаючі коливання, діють квазіпружна
сила
![]() й сила
опору
й сила
опору
![]() ,
де
,
де
![]() .
Напишіть диференціальне рівняння
загасаючих коливань.
.
Напишіть диференціальне рівняння
загасаючих коливань.
1)
![]()
2)
![]()
3)
![]()
164. Усередині системи масою
m=2 кг,
що виконує
загасаючі коливання, діють квазіпружна
сила
й сила
опору
,
де
![]() .
Напишіть диференціальне рівняння
загасаючих коливань.
.
Напишіть диференціальне рівняння
загасаючих коливань.
1)
![]()
2)
![]()
3)
![]()
165. Усередині системи масою
m=0.2 кг,
що виконує
загасаючі коливання, діють квазіпружна
сила
й сила
опору
,
де
![]() .
Напишіть диференціальне рівняння
загасаючих коливань.
.
Напишіть диференціальне рівняння
загасаючих коливань.
1)
![]()
2)
3)
166. Який вид
буде мати рішення
диференціального рівняння загасаючих
коливань
![]()
1) а; 2) б; 3) в.
|
|
|
а |
Б |
в |
167. Який вид
буде мати рішення
диференціального рівняння загасаючих
коливань
![]()
1) а; 2) б; 3) в.
|
|
|
а |
Б |
в |
168. Визначити
максимальне прискорення
матеріальної точки,
що виконує
гармонічні коливання з
амплітудою А=15 см,
якщо найбільша швидкість точки
![]()
!) 60 см/с2; 2) 30 см/с2; 3) 120 см/с2.
169. Визначити
циклічну частоту гармонічних коливань,
якщо максимальне прискорення
![]() ,
а максимальна швидкість
,
а максимальна швидкість
1) ω=4 с-1; 2) ω=2 с-1; 3) ω=6 с-1.
170. Знайти максимальну кінетичну енергію матеріальної точки масою m=2м, що виконує гармонічні коливання з амплітудою А= 4 см і частотою =5 Гц.
1) 2,28 мДж; 2) 3,28 мДж; 3) 1,58 мДж.
171. Знайти максимальну потенціальну енергію матеріальної точки масою m=2г, що виконує гармонічні коливання з амплітудою А= 4 см і частотою ω=50 Гц.
1) 0,4 мДж; 2) 1,4 мДж; 3) 2,4 мДж.
172. Складаються два коливання
однакового напрямку
й однакового періоду:
![]() .
Знайти амплітуду Ар
результуючого коливання.
.
Знайти амплітуду Ар
результуючого коливання.
1) 6 см;
2)
![]() см;
3)
см;
3)
![]() см.
см.
173. Складаються два коливання
однакового напрямку
й однакового періоду:
![]() .
Знайти амплітуду Ар
результуючого коливання.
.
Знайти амплітуду Ар
результуючого коливання.
1) 6 см; 2) см; 3) 0.
174. Складаються два коливання
однакового напрямку
й однакового періоду:
![]() .
Знайти амплітуду Ар
результуючого коливання
.
Знайти амплітуду Ар
результуючого коливання
1) 0; 2) см; 3) 6 см;
175. Дві точки знаходяться на прямій, уздовж якого поширюються хвилі зі швидкістю v=10 м/с. Період коливань Т=0.2 з, відстань між точками Δx=1 м. Знайти різницю фаз коливань у цих точках.
1) Δφ= ; 2) Δφ= ; 3) Δφ= .
176. Визначити
швидкість v
поширення
хвиль у пружному
середовищі,
якщо різниця
фаз Δφ
коливань двох точок,
що відстоять одна від одної на Δx=15
см,
дорівнює /2.
Частота коливань
![]() .
.
1) 28 м/с; 2) 51 м/с; 3) 61 м/с.
177. Поперечна хвиля поширюється уздовж пружного шнура зі швидкістю v=15 м/с. Період коливань точок шнура Т=1.2 с. Визначити різницю фаз Δφ коливань двох точок, що відстоять від джерела хвиль на відстанях x1=20 м и x2 = =30 м.
1) 1.11; 2) 2000; 3) Обидві відповіді вірні.
178. Система масою m
виконує
вимушені коливання під дією зовнішньої
періодично діючої
сили
![]() .
Усередині системи діють квазіпружна
сила
й
сила
опору
.
Скласти диференціальне рівняння
вимушених коливань, якщо m=20
г,
F0=2H,
k=100 Н/м, r= 80 Н·с/м.
.
Усередині системи діють квазіпружна
сила
й
сила
опору
.
Скласти диференціальне рівняння
вимушених коливань, якщо m=20
г,
F0=2H,
k=100 Н/м, r= 80 Н·с/м.
1)
![]() :
:
2)
![]() :
:
3)
![]() .
.
179. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Скласти диференціальне рівняння вимушених коливань, якщо m=10 г, F0=2H, k=100 Н/м, r= 80 Н·с/м.
1) :
2)
![]() :
:
3) .
180. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Скласти диференціальне рівняння вимушених коливань, якщо m=15 г, F0=2H, k=100 Н/м, r= 70 Н·с/м.
1)
![]() :
:
2)
![]() :
:
3)
![]() .
.
181. Система масою m
виконує
вимушені коливання під дією зовнішньої
періодично діючої
сили
.
Усередині системи діють квазіпружна
сила
й
сила
опору
.
Знайти резонансну частоту, якщо
k=100 Н/м, r= 0.8 Н·с/м, m=10 г. Довідка:
резонансна частота розраховується по
формулі
![]() .
.
1) 82 з-1; 2) 72 з-1; 3) 62 з-1.
181. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Знайти резонансну частоту, якщо k=100 Н/м, r= 0.9 Н·с/м, m=10 г. Довідка: резонансна частота розраховується по формулі .
1) 72.6 з-1; 2) 82.6 з-1; 3) 62.6 з-1.
182. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Знайти резонансну частоту, якщо k=100 Н/м, r= 0.7 Н·с/м, m=10 г. Довідка: резонансна частота розраховується по формулі .
1) 49.6 с-1; 2) 39.6 с-1; 3) 49.5 с-1.
183. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Чи буде спостерігатися резонанс, якщо k=100 Н/м, r= 0.7 Н·с/м, m=10 г?
1) так; 2) немає; 3) буде, якщо k=0.
184. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору . Чи буде спостерігатися резонанс, якщо k=100 Н/м, r= 7 Н·с/м, m=10 г.
1) так; 2) немає; 3) буде, якщо k=0.
185. У загальному
випадку зміна
частоти звукових хвиль в ефекті Доплера
визначається
формулою:
![]() .
Яку частоту зареєструє нерухомий
приймач, якщо джерело наближається до
нього
зі
швидкістю 50
м/с?
Швидкість
звуку в повітрі прийняти рівної
340
м/с;
.
Яку частоту зареєструє нерухомий
приймач, якщо джерело наближається до
нього
зі
швидкістю 50
м/с?
Швидкість
звуку в повітрі прийняти рівної
340
м/с;
![]()
1) 115 Гц; 2) 117 Гц; 3) 116 Гц.
186. У загальному випадку зміна частоти звукових хвиль в ефекті Доплера визначається формулою :. Яку частоту зареєструє нерухомий приймач, якщо джерело віддаляється від нього зі швидкістю 50 м/с? Швидкість звуку в повітрі прийняти рівної 340 м/с; .
1) 87 Гц; 2) 117 Гц; 3) 115 Гц.
187. У загальному випадку зміна частоти звукових хвиль в ефекті Доплера визначається формулою: . Яку частоту зареєструє приймач, якщо він наближається до джерела зі швидкістю 50 м/с? Швидкість звуку в повітрі прийняти рівної 340 м/с; .
1) 117 Гц; 2) 115 Гц; 3) 87 Гц.
188. У загальному випадку зміна частоти звукових хвиль в ефекті Доплера визначається формулою: . Яку частоту зареєструє приймач, якщо він віддаляється від джерела зі швидкістю 50 м/с? Швидкість звуку в повітрі прийняти рівної 340 м/с; .
1) 85 Гц; 2) 87 Гц; 3) 115 Гц.
189. Система
масою m
виконує
вимушені коливання під дією зовнішньої
періодично діючої
сили
.
Усередині системи діють квазіпружна
сила
й
сила
опору
,
де k=100 Н/м, r= 0.7 Н·с/м.,
m=10 г,
![]() =
100 с-1.
Чому дорівнює початкова фаза вимушених
коливань? Довідка: початкова фаза
вимушених коливань знаходиться по
формулі
=
100 с-1.
Чому дорівнює початкова фаза вимушених
коливань? Довідка: початкова фаза
вимушених коливань знаходиться по
формулі
![]() .
.
1) φ = π; 2) φ = π/2; 3) φ = 0;
190. Система масою m виконує вимушені коливання під дією зовнішньої періодично діючої сили . Усередині системи діють квазіпружна сила й сила опору , де k=100 Н/м, r= 1.5 Н·с/м., m=10 г, = 50 с-1. Чому дорівнює початкова фаза вимушених коливань? Довідка: початкова фаза вимушених коливань знаходиться по формулі .
1) φ = π; 2) φ = π/2; 3) φ = π/4.
191. Електропоїзд проходить повз нерухомий приймач і дає гудок, частота якого 300 Гц. Приймаючи швидкість звуку рівною 340 м/с, визначте швидкість електропоїзда, якщо приймач реєструє частоту 334 Гц.
1) 34.6 м/с; 2) 44.5 м/с; 3) 54.5 м/с.
192. Дві точки знаходяться від джерела коливань на відстанях x1=4 м и x1=7 м . Період коливань Т=20 мс і швидкість поширення хвилі дорівнює 300 м/с. Визначите різницю фаз коливань цих точок.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.