3.6.3. Силовой расчет группы звеньев 2−3

Отделим от механизма группу звеньев 2−3, разорвав связи звена 3 в шарнире Е со стойкой, а связи звена 2 в шарнире А со звеном 1 (рис. 3.20).

Действие стойки на звено 3 заменим силой реакции , которую разложим на две составляющие: нормальную (направим вдоль звена ВЕ) и касательную (направим перпендикулярно ВЕ). Действие звена 1 на звено 2 заменим силой , которую также разложим на две составляющие: нормальную (направим вдоль АВ) и касательную (направим перпендикулярно АВ). Действие звена 4 на звено 2 заменим реакцией связи , которая равна по модулю и противоположна по направлению силе .

Рис. 3.20

Таким образом, мы имеем четыре неизвестные величины сил , , , направление которых известно. Для определения силы запишем уравнение суммы моментов сил, действующих на звено 2, относительно точки В ( ):

,

отсюда получим:

Для определения силы запишем уравнение суммы моментов сил, действующих на звено 3, относительно точки В ( ):

,

отсюда получим:

Для определения сил и , а в итоге и полных сил и запишем векторное уравнение суммы сил, действующих на звенья 2 и 3 ( ):

.

Решим это уравнение графически, для чего зададим масштабный коэффициент . Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.7.

Таблица 3.7

Силы
Действительная величина, Н	45,4	90,64	392,7	733	36,79	60,94	3,1
Масштабная величина, мм	9,1	18,1	78,5	146,6	7,4	12,2	0,6

Построим план сил. Из намеченной точки отложим по порядку с соответствующими направлениями векторы, изображающие силы в масштабе, , , , , , , (рис. 3.21). Для того чтобы замкнуть многоугольник сил, через начало вектора проведем линию, параллельную направлению силы (параллельно АВ), а через конец вектора проведем линию, параллельную направлению силы (параллельно ВЕ). В результате пересечения этих линий получим отрезки, изображающие силы и . Направим векторы сил по обходу контура.

В результате сложения нормальных и касательных составляющих получим полные силы и . Модули этих сил определим по формулам:

Рис. 3.22

Для определения силы, действующей со стороны звена 2 на звено 3, т. е. реакции связи ( ), запишем векторное уравнение суммы сил, действующих на звено 3 ( ):

.

Соединим начало вектора с концом вектора . Полученный отрезок изобразит силу в масштабе:

3.6.4. Силовой расчет ведущего звена

Отделим от механизма ведущее звено 1, разорвав связь этого звена в шарнире О со стойкой (рис. 3.22). Действие стойки на звено 1 заменим силой реакции связи , а звена 2 – силой , которая равна по модулю и противоположна по направлению силе . К ведущему звену приложим уравновешивающий момент , который направим в сторону вращения, так как он является движущим. Для определения этого момента запишем уравнение суммы моментов сил, действующих на ведущее звено, относительно точки О ( ):

,

отсюда получим

Для определения реакции связи запишем векторное уравнение суммы сил, действующих на звено 1 ( ):

.

Решим это уравнение графически, для чего зададим масштабный коэффициент . Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.8.

Таблица 3.8

Силы
Действительная величина, Н	7,85	230
Масштабная величина, мм	3,9	115

Построим план сил. Из намеченной точки отложим по порядку с соответствующими направлениями векторы, изображающие силы в масштабе: , (рис. 3.24). Для того чтобы замкнуть многоугольник сил, соединим начальную точку с концом последнего отложенного вектора. Полученный отрезок изобразит силу . Направим вектор по обходу контура. Модуль силы

Рис. 3 23

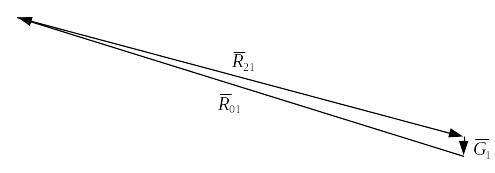
Рис. 3.24