2.2.5. Определение скоростей и ускорений точек механизма, угловых скоростей и угловых ускорений звеньев механизма

При определении скоростей и ускорений точек механизма следует использовать зависимости между скоростями и ускорениями точек звеньев механизма. Эти зависимости определяются видом движения звена.

Поступательное движение тела – это движение тела, при котором любая прямая этого тела перемещается параллельно самой себе.

При поступательном движении тела скорости всех точек тела одинаковы ( ), одинаковы и ускорения точек ( ) (рис. 2.11).

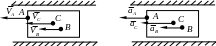
Рис. 2.11

Вращательное движение тела – это движение, при котором все точки тела движутся по окружностям, перпендикулярным прямой, называемой осью вращения (рис. 2.12).

При вращательном движении тела скорость любой точки А этого тела направлена перпендикулярно ее радиусу вращения и вычисляется по формуле

г де – угловая скорость вращения тела; R – радиус вращения точки А (расстояние от точки А до оси вращения О).

Рис. 2.12 Рис. 2.13

Ускорение любой точки А вращающегося тела представляется в виде двух составляющих:

• нормального ускорения 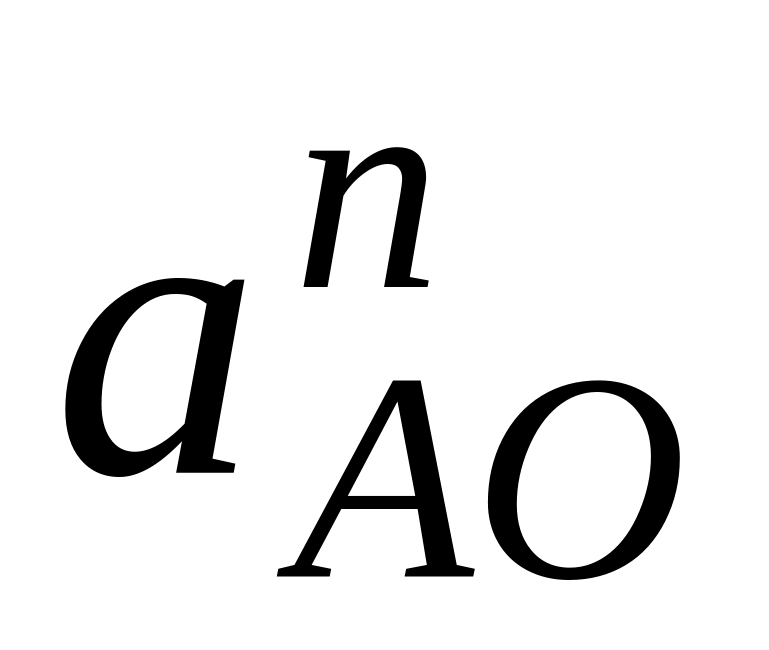, направленного к оси вращения (рис. 2.13):

• касательного ускорения 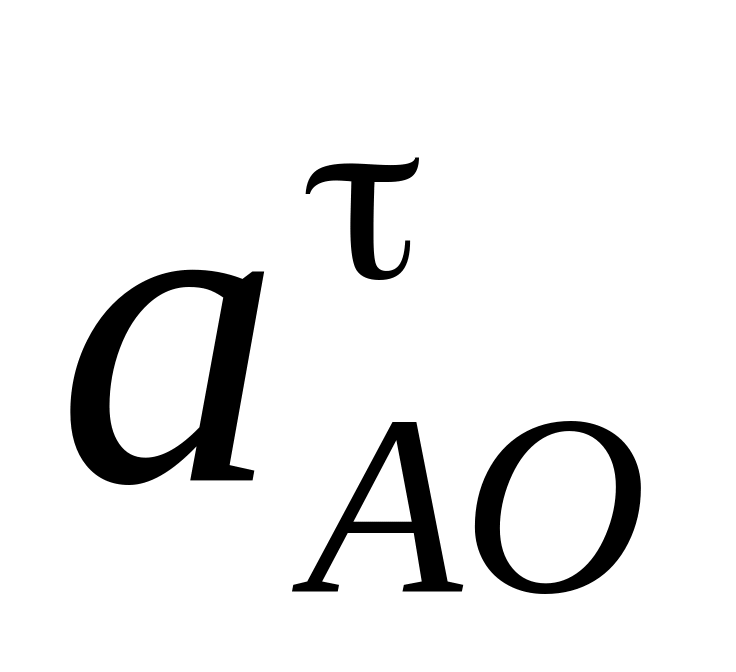, направленного перпендикулярно радиусу вращения точки (рис. 2.13):

где − угловое ускорение звена.

Полное ускорение любой точки вращающегося тела (например, точки А)

Плоскопараллельное движение тела – это движение тела, которое можно представить состоящим их двух одновременно происходящих в одной плоскости движений:

• поступательного движения тела со скоростью какой-либо его точки, называемой полюсом;

• вращательного движения тела вокруг полюса.

Для определения скорости и ускорения любой точки тела, совершающего плоскопараллельное движение, необходимо знать скорость и ускорение полюса.

Тогда, согласно определению плоскопараллельного движения тела, скорость любой точки этого тела (например, точки В) будет определяться через скорость полюса (пусть им будет, например, точка А) следующим образом (см. рис. 2.14):

(2.29)

где – скорость точки В; – скорость точки А, взятой за полюс; – скорость вращения точки В вокруг точки А.

Рис. 2.14 Рис. 2.15

Так как – скорость вращения точки В вокруг точки А, то можно записать

Скорость направлена перпендикулярно радиусу вращения точки В, т. е. перпендикулярно АВ.

Аналогично записывается и ускорение любой точки плоскодвижущегося тела (например, точки В), выраженное через ускорение полюса (точки А) (рис. 2.15):

, (2.30)

где − ускорение точки В при ее вращении вокруг точки А.

Ускорение можно представить в виде

(2.31)

где − нормальное ускорение точки В при ее вращении вокруг точки А, направленное к точке А;

− тангенциальное ускорение точки В при ее вращении вокруг точки А, направленное перпендикулярно радиусу вращения АВ;

.

Полное ускорение точки В с учетом выражения (2.31) можно записать и как

. (2.32)

Сложное движение точки − это движение, при котором точка одновременно участвует в двух или более движениях.

Движение точки по подвижному телу называется относительным движением точки.

Движение тела, по которому перемещается точка, называется переносным движением точки.

Движение точки относительно неподвижной системы отсчета, связанной со стойкой, называется абсолютным движением точки.

Рассмотрим кулисный механизм (рис.2. 16, a), состоящий из трех подвижных тел: кривошипа ОА₁, кулисы О₁В и камня кулисы А₁.

На кулисе О₁В под точкой А₁ будет находиться точка А₃ (рис. 2.16, б), принадлежащая звену. При вращении кулисы О₁В точка А₁ камня кулисы перемещается вдоль кулисы. Точно так же будет изменять свое положение на кулисе и точка А₃, все время находясь под точкой А₁.

О движении точки А₁ камня кулисы по кулисе О₁В можно говорить как о движении точки А₁ относительно точки А₃ кулисы. Поэтому скорость и ускорение движения точки А₁ по кулисе записывают как и .

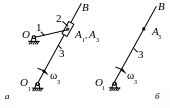
Рис. 2.16

Точка А₁ изображенного на рис. 2.16, а механизма принадлежит одновременно и кривошипу 1 и камню кулисы 2.

Расчленим механизм на отдельные части (рис.2. 17). Рассмотрим движение точки А₁ звена 1 относительно неподвижной оси О – это абсолютное движение точки А₁, принадлежащей звену 1 (рис. 2.17, а) и звену 2 (рис. 2.17, б).

Вращательное движение точки А₁ звена 1 относительно неподвижной оси О – это абсолютное движение точки А₁ со скоростью .

Движение точки А₃ звена 3 (рис. 2.17, б) является движением сложным, состоящим из относительного (поступательного) движения точки А₃ по кулисе О₁В (со скоростью ) и переносного (вращательного) движения точки А₁ вместе с кривошипом ОА вокруг оси О (со скоростью ). План скоростей представлен на рис. 2.17, в.

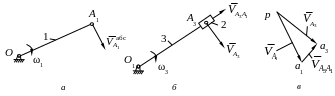
Рис. 2.17

Как известно из курса теоретической механики, при сложном движении точки ее абсолютную скорость и ускорение вычисляют по формулам

, (2.33)

. (2.34)

Для механизма, изображенного на рис. 2.16, зависимости (2.33) и (2.34)имеют вид

, ,

где – ускорение Кориолиса.

Для плоских механизмов величину ускорения Кориолиса определяют по зависимости

Для нахождения направления ускорения Кориолиса вектор относительной скорости нужно повернуть в плоскости механизма на 90^ᴼ в сторону переносного вращения. Для механизма, изображенного на рис. 2.18, а, покажем направление ускорения Кориолиса точки А₃ и запишем выражение для определения величины этого ускорения:

. (2.35)

На рис. 2.18, а показано, как определяется ускорение Кориолиса , на рис. 2.18, б – ускорения этой точки, на рис. 2.18, в – план ускорений.

Рис. 2.18

Таким образом, скорость точки А₃ определяется по формуле

(2.36)

где – абсолютная скорость точки А₃, направленная перпендикулярно звену ОВ₁; – переносная скорость точки А₁, вращающейся вместе с кривошипом вокруг оси О; – относительная скорость движения точки А₃ по кулисе О₁В (см. рис. 2.17, в).

Из рис. 2. 18, б следует

, (2.37)

где – абсолютное ускорение точки А₃, полученное путем геометрического сложения слагаемых векторов; − переносное ускорение точки А₁, вращающейся вместе с кривошипом ОА вокруг оси О; – относительная скорость точки А₃ при движении ее вдоль кулисы О₁В; – ускорение Кориолиса точки А₃.