2.2.4. Построение графиков перемещений, скоростей и ускорений ведомого звена

График перемещений ведомого звена нетрудно построить по известным 12 положениям этого звена, взяв за начало отсчета перемещений одно из крайних положений ведомого звена механизма.

График перемещений ведомого звена обычно строят в зависимости от угла поворота ведущего звена. При этом если ведомое звено В совершает поступательное движение (рис. 2.7, а), то график перемещений звена В изображает зависимость линейного перемещения этого звена от угла поворота ведущего звена, т. е. (рис. 2.7, б). Если ведомое звено ВС совершает вращательное движение (рис. 2.8, а), то график перемещений звена ВС изображает зависимость углового перемещения этого звена от угла поворота ведущего звена, т. е. (рис. 2.8, б).

Р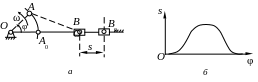 ис. 2.7

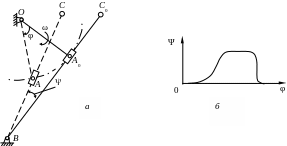
Рис. 2.8

График перемещений строят в масштабе. Масштабный коэффициент при этом принимают отдельно как для угла откладываемого по оси абсцисс, так и для перемещений s или откладываемых по оси ординат (рис. 2.7, б).

Масштабным коэффициентом называется отношение действительной величины к длине отрезка, изображающего эту величину. Так, например, если угол , равный рад, отложить на оси абсцисс в виде отрезка 62,8 мм, то масштабный коэффициент при этом будет

Это значит, что 1 мм отрезка на оси абсцисс соответствует углу 0,1 рад.

Масштабный коэффициент должен выражаться числом с одной значащей цифрой, например: 0,02; 0,2; 2,0; 20 и т. д.

Если графически продифференцируем график перемещения ведомого звена по углу поворота ведущего звена, то получим график, называемый графиком аналога скорости ведомого звена. По значению аналога скорости нетрудно найти скорость ведомого звена:

.

Отсюда

или

, (2.21)

где – скорость ведомого звена; – угловая скорость ведущего звена. Аналогично для углового перемещения ведомого звена имеем

Отсюда

или

. (2.22)

Зависимости (2.21) и (2.22) показывают, что скорость ведомого звена, совершающего поступательное или вращательное движение, равна произведению аналога скорости этого звена на угловую скорость ведущего звена.

Для нахождения аналога ускорения ведомого звена следует графически продифференцировать график аналога скорости этого звена по углу поворота ведущего звена.

В случае равномерного вращения ведущего звена по значению аналога ускорения ведомого звена нетрудно найти ускорение этого звена. Для поступательного перемещения ведомого звена получим:

отсюда

или

. (2.23)

Аналогично для углового перемещения ведомого звена:

отсюда

,

или

(2.24)

Зависимости (2.23) и (2.24) показывают, что при равномерном вращении ведущего звена ускорение ведомого звена, совершающего поступательное или вращательное движение, равно произведению аналога ускорения этого звена на квадрат угловой скорости ведущего звена.

Графическое дифференцирование обычно проводят двумя методами: методом хорд и методом касательных.

Рассмотрим метод хорд на примере графического дифференцирования графика перемещений.

Пусть задан график перемещений ведомого звена (рис. 2.9, а). Масштабные коэффициенты – по оси абсцисс и – по оси ординат известны. Разобьем ось абсцисс (ось ) на ряд одинаковых отрезков, например на 12. Под графиком перемещений проведем оси координат, в которых будем строить график аналога скорости ведомого звена. Hа каждом отрезке кривую графика заменим ее хордой. На оси абсцисс этой системы координат влево от оcи ординат отложим произвольный отрезок Н₁, который назовем полюсным расстоянием, и затем из начальной точки О₁ этого отрезка (см. рис. 2.9, б) проведем прямые, параллельные хордам графика перемещений. Эти прямые пересекут ось ординат в точках 1−12. Из точек 1−12 проведем горизонтальные прямые на соответствующих участках I, II, III. Горизонтальный отрезок 1−1' на участке I разделим точкой А на равные части, также поступим и с горизонтальным отрезком 2'−2" на участке II. Получим точку В. Аналогично определим точки и для всех остальных участков. Соединив плавной кривой точки А, В и т. д., получим график аналога скорости ведомого звена (рис. 2.9, б). Ось абсцисс этого графика представляет собой ось углов поворота ведущего звена, а ось ординат – ось аналога скорости ведомого звена. Масштабный коэффициент для оси абсцисс равен , а для оси ординат – .

Для графика перемещений известны масштабные коэффициенты:  − для углов ; – для перемещений S. После графического дифференцирования графика перемещений масштабный коэффициент для оси абсцисс остается без изменения, а масштабный коэффициент для оси ординат (оси аналога скорости) определим по формуле

(2.25)

При угловом перемещении ведомого звена масштабный коэффициент для оси аналога скорости

(2.26)

Для получения масштабного коэффициента или в виде числа с одной значащей цифрой необходимо подобрать соответствующее полюсное расстояние Н₁ в формулах (2.25), (2.26).

Р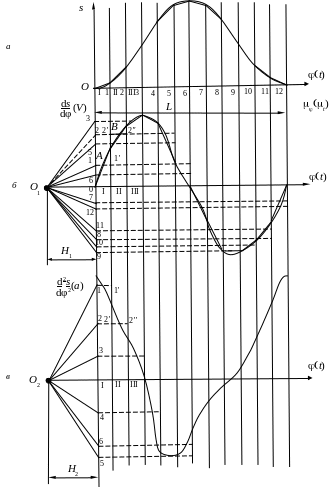 ис. 2.9

Продифференцировав график аналога скорости по методу хорд (рис. 2.9, б), получим график аналога ускорения ведомого звена (рис. 2.9, в). Масштабный коэффициент для оси ординат полученного графика (оси аналога ускорения) определим по формулам:

а) для линейного перемещения ведомого звена

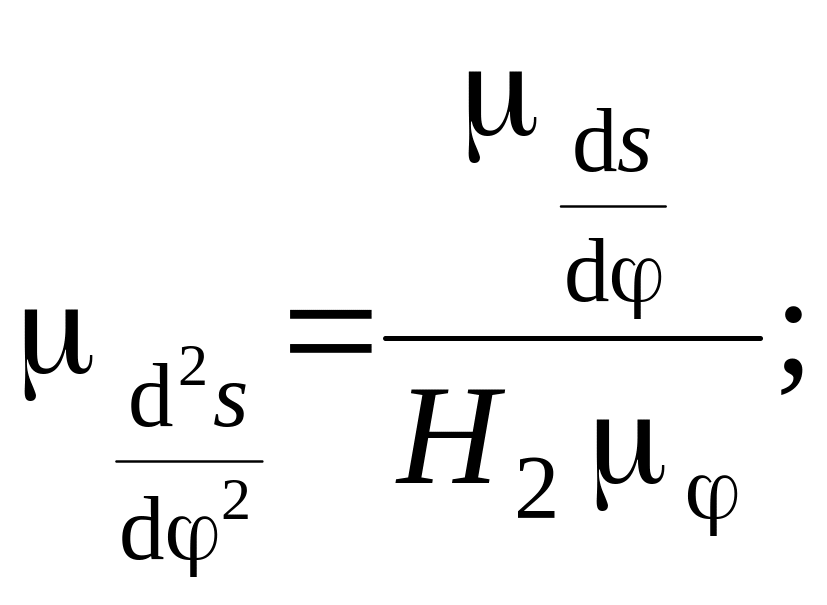(2.27)

б) для углового перемещения ведомого звена

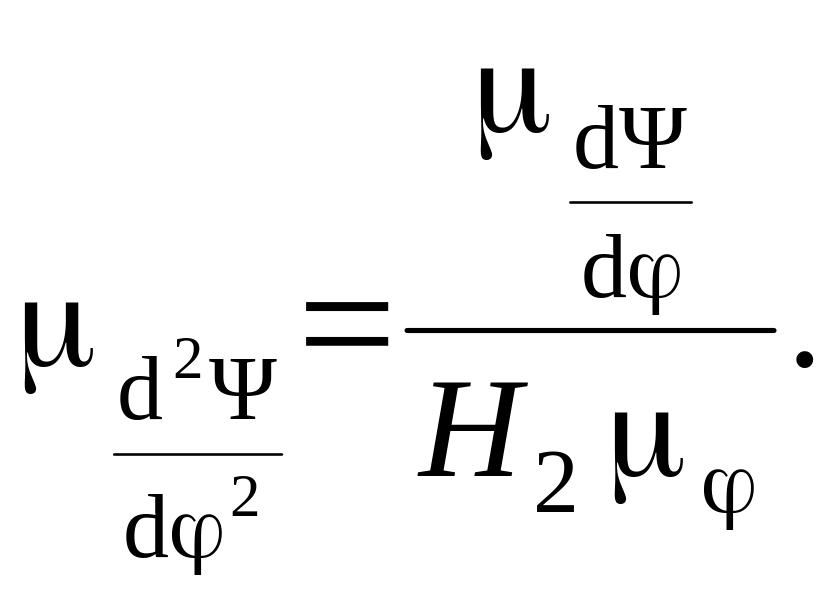(2.28)

Так как графики s, и связаны между собой дифференциальной зависимостью, то к ним применимы все закономерности, существующие между функцией и ее производной. Приведем некоторые из этих закономерностей:

1. если функция возрастает, то ее первая производная положительна;

2. если первая производная непрерывной функции в какой-либо точке равна нулю, то в этой точке функция имеет экстремумы;

3. если непрерывная функция имеет точки перегиба, то первая производная этой функции в данных точках имеет экстремумы, а вторая производная равна нулю;

4. если для непрерывной функции значение первой производной в данной точке больше, чем значение производной в другой точке, то кривая функции в первой точке более крутая, чем во второй, так как ;

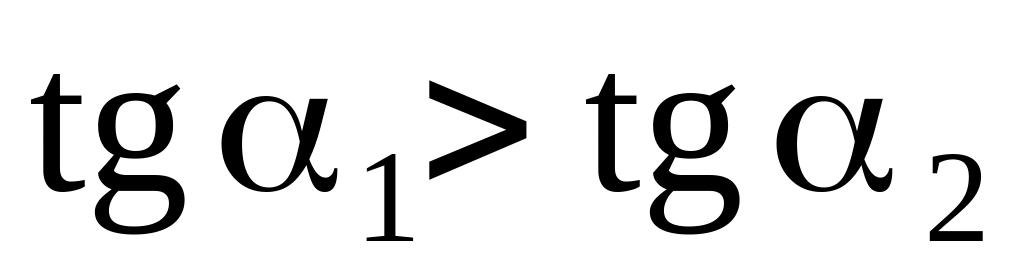5. если функция непрерывна и не имеет скачков, то ее первая производная – плавная кривая.

При графическом дифференцировании, в результате замены кривой функции ступенчатой ломаной линией, появляется погрешность в построении производных функций. Для уменьшения этой погрешности необходимо, чтобы хорды, которыми заменяются на своих отрезках кривые функции, незначительно отличались от этих кривых. С этой целью тот участок АВ (рис. 2.10), где хорда аb существенно отличается от кривой аb, необходимо разбить на более мелкие участки (АС; СD; DВ), в которых хорды и кривые имеют незначительные отличия.

П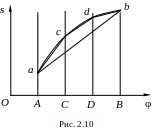 ример 2.3. Найти масштабные коэффициенты для аналога скорости и аналога ускорения ведомого звена, если известны ; Н₁ = 30 мм, Н₂ = 40 мм.

Решение. Используя формулу (2.25), найдем масштабный коэффициент аналога скорости:

По формуле (2.27) найдем масштабный коэффициент аналога ускорения:

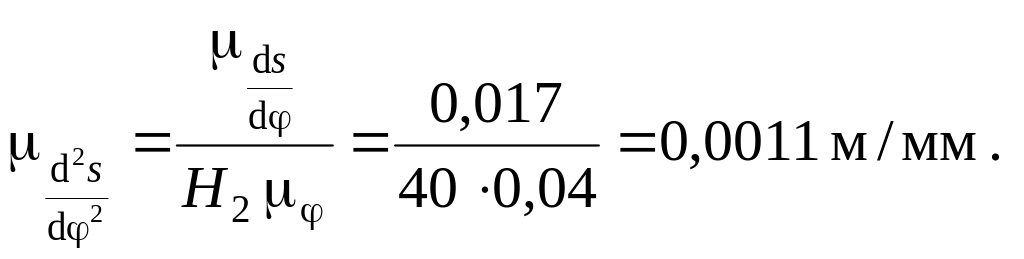
Пример 2.4. Найти значения полюсных расстояний Н₁ и Н₂ для получения масштабных коэффициентов и если известны

и

Решение. Воспользовавшись формулой (2.25), найдем Н₁:

.

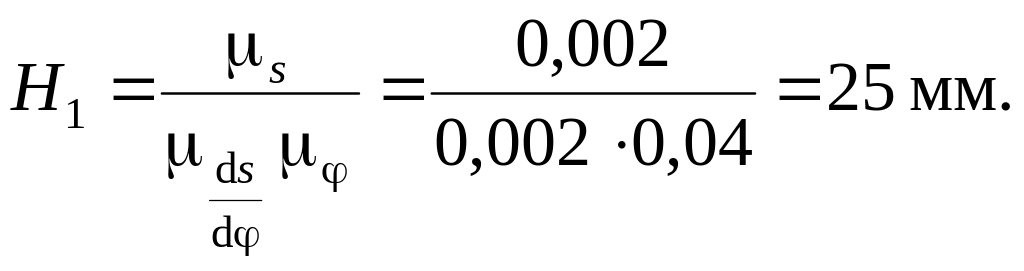
Используя формулу (2.27), определим Н₂:

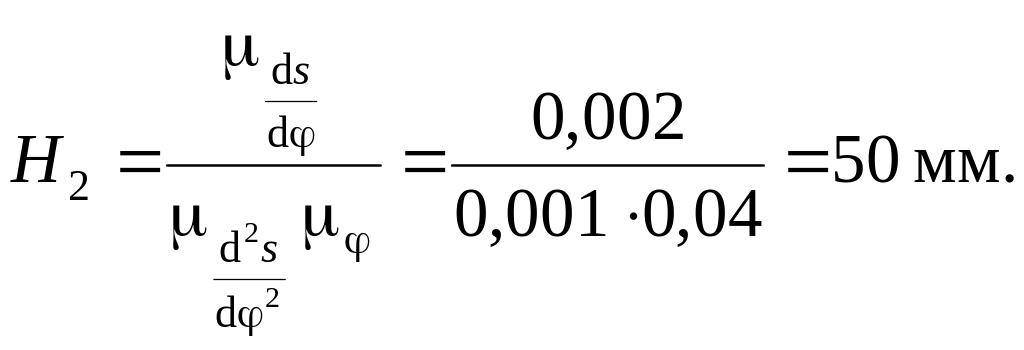
Пример 2.5. Определить скорость и ускорение ведомого звена, совершающего поступательное движение, если известны в данный момент времени аналог скорости и аналог ускорения этого звена:

, .

Угловая скорость ведущего звена

Решение. По зависимости (2.21) найдем скорость ведомого звена:

По зависимости (2.23) определим ускорение ведомого звена:

Если на оси абсцисс вместо угла поворота откладывается время t, то при графическом дифференцировании получим графики скорости и ускорения . Для определения масштабного коэффициента необходимо определить сначала период Т – время одного полного оборота, с

где n – частота вращения ведущего звена, об/мин.

Тогда масштабный коэффициент, с/мм

где L – длина отрезка, на котором отложено время, равное периоду Т.