1.8. Структурный анализ плоского рычажного шестизвенного механизма с качающейся кулисой

Кинематическая схема рычажного механизма представлена на рис.1.11.

Рис. 1.11

Исходные данные: .

1.8.1. Количество и названия звеньев механизма

Определим звенья, входящие в механизм:

1 – кривошип (совершает вращательное движение, полный оборот);

2 – шатун (совершает плоско-параллельное движение);

3 – коромысло (вращательное движение, неполный оборот);

4 – кулисный камень (относительное поступательное движение вдоль кулисы);

5 − кулиса (вращательное движение);

0 – стойка (неподвижные части механизма).

1.8.2. Количество и характер кинематических пар

В данном механизме (рис. 1.11) все пары низшие, пятого класса. Будем обозначать низшие вращательные пары – НВП, а низшие поступательные – НПП.

О − НВП звеньев 0−1;

А − НВП звеньев 1−2;

В − НВП звеньев 2−3;

Е − НВП звеньев 3−0;

С − НВП звеньев 2−4;

− НПП звеньев 4−5;

F − НПП звеньев 5−0.

Степень подвижности механизма определим по формуле Чебышева

где n = 5; р₅ = 7; р₄ = 0.

Степень подвижности механизма равна единице. Это значит, что механизм имеет одно ведущее звено.

1.8.3. Разложение механизма на группы Ассура

Начнем разложение механизма на группы Ассура с последних звеньев.

Данная группа (рис. 1.12) состоит из звеньев 4 и 5. Это структурная группа II класса, 2-го порядка (двухповодковая), вида 3. Данная группа имеет n = 2, р₅ = 3, W = 0.

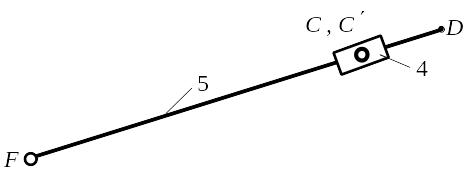
Рис. 1.12

Выделим из механизма вторую структурную группу (рис. 1.13), которая состоит из звеньев 2 и 3. Это структурная группа II класса, 2-го порядка, вида 1. Данная группа имеет n = 2, р₅ = 3, W = 0.

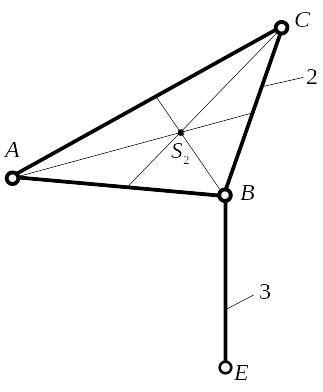
Рис. 1.13

Нулевое звено (стойка) вместе с первым (ведущим) звеном образуют ведущий механизм I класса (рис. 1.14), который имеет n = 1; р₅ = 1, W = 1.

Рис. 1.14

Вывод: рассматриваемый механизм является механизмом второго класса. Формула его построения имеет вид

где римскими цифрами указан класс групп звеньев.