1.5. Замена высших пар низшими в плоском механизме

В плоских механизмах высшую пару условно можно заменить низшими кинематическими парами. Это делают для удобства структурного или кинематического расчета.

Рассмотрим схему плоского механизма с высшей кинематической парой (рис. 1.4, а). В точке К звенья 1 и 2 образуют высшую кинематическую пару. Для замены высшей пары низшими необходимо соблюсти два условия: сохранить ту же степень подвижности механизма и характер мгновенного относительного движения звеньев.

а б

Рис. 1.4

Алгоритм замены высших кинематических пар низшими:

1. Из точки касания К провести общую нормаль к кривым элементов кинематических пар (рис. 1.4, а).

2. Определить положение центров кривизны А и В кривых в данной точке К.

3. В центрах кривизны А и В поместить вращательные пары.

4. Соединить центры А и В прямой и получить отрезок АВ, который явится фиктивным звеном.

5. Соединить центры А и В с центрами (осями) вращения звеньев 1 и 2 (рис. 1.4, б).

Таким образом, вместо механизма, представленного на рис. 1.4, а), получим заменяющий механизм, приведенный на рис. 1.4, б. Одна высшая пара заменяется группой, состоящей из одного фиктивного звена и двух низших пар. Данная замена справедлива только для заданного положения механизма.

В случае если один элемент кинематической пары плоский (линия), то центр кривизны такого элемента находится в бесконечности. Тогда в точке касания К (рис. 1.5) помещается поступательная пара.

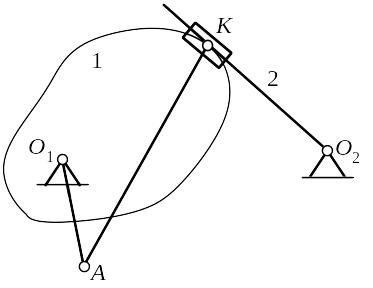
Рис. 1.5

1.6. Принцип образования плоских механизмов (по Ассуру)

В 1914 году профессор Петроградского политехнического института Л.В. Ассур(1878−1920) предложил все кинематические цепи разбить на две группы:

1. Кинематические цепи с одним подвижным звеном и стойкой;

2. Кинематические цепи с нулевой степенью подвижности.

Представим характеристику цепи с одним подвижным звеном и стойкой (рис. 1.6):

а) звено 1, представленное на рис. 1.6, а, совершает простейшее вращательное движение, на рис. 1.6, б – поступательное;

б) степень подвижности этой цепи равна единице;

в) задан закон движения звена:  = (t), S = S(t).

а б

Рис. 1.6

Кинематическая цепь на рис. 1.6 называется механизмом первого класса. Первое звено чаще всего бывает ведущим. Независимую координату, определяющую положение этого звена, называют обобщенной координатой. В механизме может быть несколько таких звеньев, называемых группой начальных звеньев.

Используя возможность замены высших пар низшими, перепишем формулу Чебышева (1.3) в виде

,

где n − число подвижных звеньев; p₅ − число пар пятого класса.

Для группы Ассура получим уравнение

,

из которого определим соотношение между числом звеньев и числом кинематических пар в группе Ассура:

. (1.5)

Из формулы (1.5) видно, что если р₅ и n − целые числа, то n может быть только четным числом.

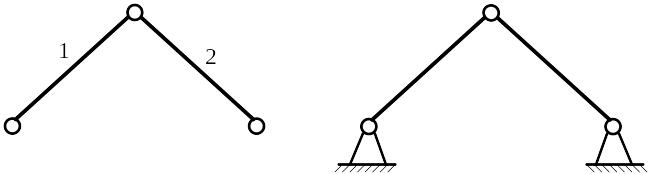
а б

Рис. 1.7

Представим другую характеристику кинематической цепи с нулевой степенью подвижности − группы Ассура, представленной на рис. 1.7, а:

а) степень подвижности группы равна нулю (W = 0);

б) при присоединении группы Ассура к стойке образуется неподвижное соединение − ферма (рис. 1.7, б);

в) в цепи должно быть обеспечено определенное соотношение между числом подвижных звеньев и числом кинематических пар (см. формулу (1.4)).