билеты 1 сем / 67-72

67. Достаточный признак выпуклости графика функции

Определение: Функция выпукла вниз (вверх) на интервале, если все точки дуги её графика на этом интервале лежат под (над) соответствующей хордой или на ней (по Фихтенгольцу).

68. Теорема о касательной к графику выпуклой функции

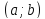График функции имеет на интервале выпуклость, направленную вниз (вверх), если график этой функции в пределах 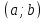лежит не ниже (не выше) любой своей касательной (Лемма 1 по Ильину-Позняку).

Замечание 1: термин «не ниже» имеет смысл, ибо касательная не параллельна оси Oy.

Теорема: Если функция 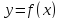имеет на интервале 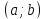конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции 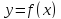имеет на интервале 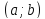выпуклость, направленную вниз (вверх).

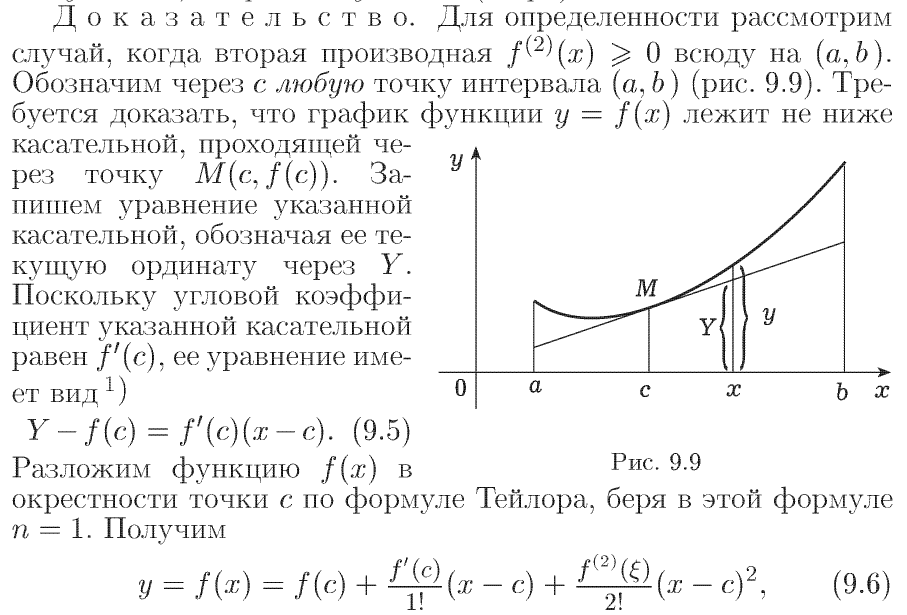
69. Необходимый признак точки перегиба. Пример

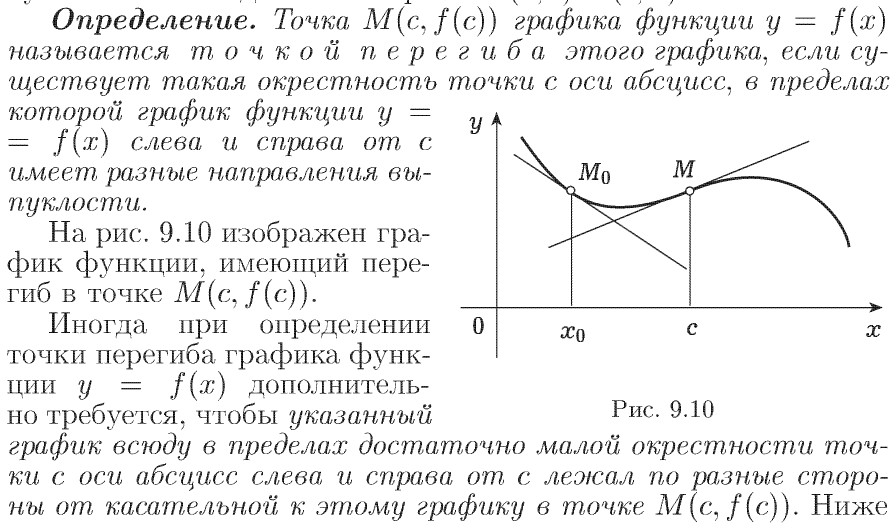
Замечание: этого условия недостаточно, и оно не всегда выполняется.

Пример 2: 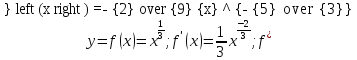. Здесь в нуле второй производной не существует, однако 0 – точка перегиба.

70. Достаточный признак точки перегиба. Пример

Первый признак:

Второй признак: (если неясен знак второй производной в окрестности с)

Проще говоря, точка перегиба – это точка, в которой меняется характер выпуклости (то есть 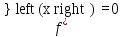или не существует).

71.Теорема о наклонных асимптотах. Пример

Определение: Пусть функции 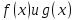определены на 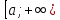и они – б.б.ф. (бесконечно большие функции) при 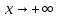. Тогда эти функции асимптотически равны , если 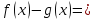б.м.ф. (бесконечно малая функция) при 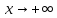. Аналогично и с .

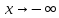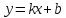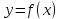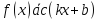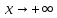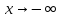Прямая – асимптота функции , если они асимптотически равны: при (или ) или .

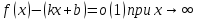Нахождение наклонной асимптоты:

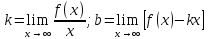
Пример:

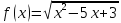
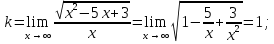
Наклонная асимптота:

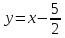
Следует отдельно упомянуть вертикальную асимптоту:

72. Общая схема исследования функции и построения её графика по характерным точкам на примере функции

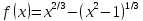
1. Найти область определения функции, область значений, чётность функции.

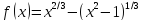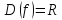: - непрерывная функция, х принимает любые значения;

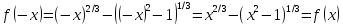– чётная функция; следовательно, можно рассмотреть только положительную часть (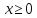), зная, что отрицательная ей симметрична.

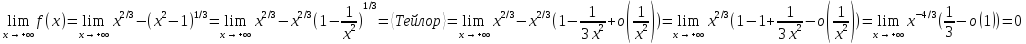
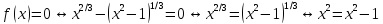– ложное высказывание, тогда 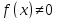, то есть функция сохраняет знак (и имеет место горизонтальная асимптота у=0): для определения знака возьмём х=+1:

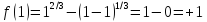– функция строго положительна:

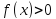
(Кстати, график функции проходит через точку (1;1))

2. Найти первую производную от функции, её область определения, определить точки экстремума (или точки, подозрительные на экстремум).

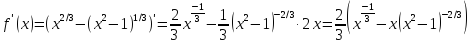
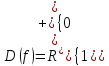(если рассматривать только неотрицательную часть)

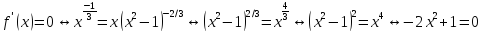
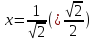– точка максимума (в ней производная меняет знак с + на -).

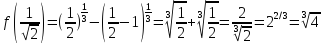
Теперь рассмотрим внимательнее точку х=0.

При переходе через неё функция 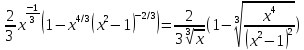меняет знак с – на + (меняется только 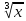), значит, х=0 – точка локального минимума.

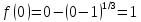(касательная в этой точке параллельна Оу (х=0)

В нашем случае точку х=1, где производная не существует, надо исследовать дальше с помощью 2-й производной.

3. Найти вторую производную от функции, её область определения, определить точки перегиба (при необходимости уточнить точки экстремума).

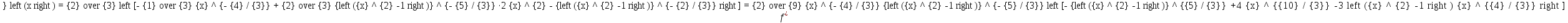
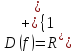
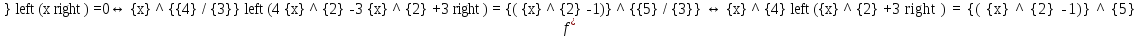
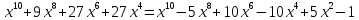
Точки перегиба: 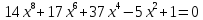: первые 2 члена с чётной степенью, то есть больше 0; оставшиеся члены образуют биквадратное уравнение с отрицательным дискриминантом, тоже больше 0. Тогда вторая производная не равна нулю.

Однако у нас есть точка х=1, где 2-я производная не существует. Поскольку при прохождении через эту точку 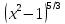меняет знак, а другие части нет, то и вся вторая производная меняет знак, тогда х=1 – точка перегиба. Мы уже знаем её координаты (1; 1) То, что первая производная в этой точке не существует, означает лишь, что касательная к графику в этой точке параллельна оси Оу (её уравнение х=1).

4. По полученным результатам построить график функции (сначала отметить стационарные точки и точки перегиба; затем провести в этих точках касательные к кривой; в конце провести схематически саму кривую).

В нашем случае начнём с положительной половины графика (функция чётная). Мы имеем:

1. Минимум 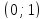(касательная );

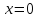2. Максимум 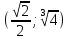(касательная );

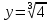3. Перегиб 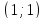(касательная );

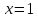4. Асимптота .

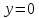Получаем:

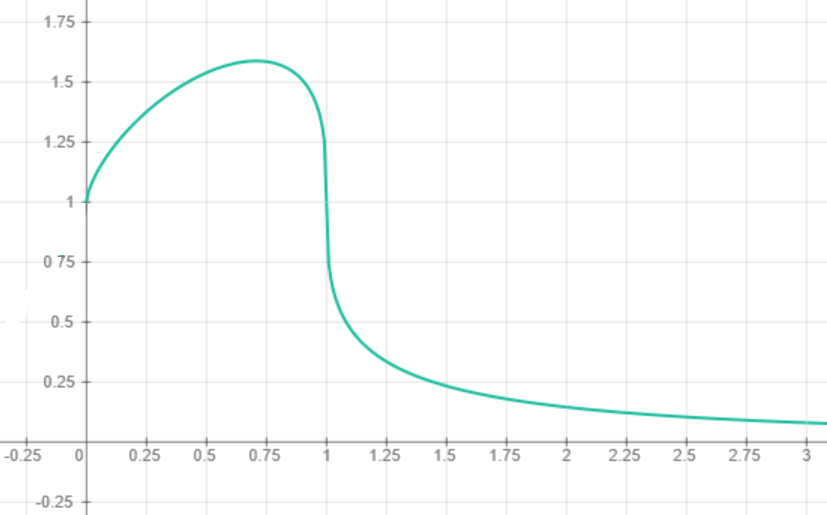
Общий вид графика целиком: