3 Практичне заняття 3 Застосування теорії подібності і розмірностей для знаходження критеріїв подібності процесів

1. Загальні відомості

У теорії подібності велике значення мають комплекси величин, що мають за себе добуток різних ступенів цих величин. Їх називають критеріями подібності і позначають літерою  (пі).

Критерії подібності використовують як параметри і змінні системи, що досліджується. Тут постає важливе питання - скільки незалежних між собою критеріїв можна утворити з n розмірних величин для процесу, що розглядається . Для знаходження критеріїв подібності існує багато способів.

Розглянемо метод нульових розмірностей при отриманні критеріїв подібності на прикладі задачі змушеного механічного коливання з демпфіруванням.

2. Метод нульових розмірностей

Тягар масою m (рис. 3.1) коливається на пружині жорсткістю с у в'язкому середовищі, сила опору якого . На тягар діє збурна сила . Переміщення тягаря х є функцією цих величин та часу t:

Рис. 3.1 - Коливання з демпфіруванням підвішеного до пружини тягара

. (3.1)

Розмірність даних величин

• х (м) - переміщення тягаря;

• m (кг) - маса тягаря;

• k (кг/с) - коефіцієнт опору середовища;

• t (с) - час;

•  (1/с) - частота коливань;

• F₀ (кг-м/с²) - збурна сила;

• с (кг/с²) - жорсткість пружини.

Згідно з цим методом необхідно вибрати за числом основних одиниць таке ж саме число параметрів з записаної сукупності, для яких визначник, що складений з показників ступіней основних одиниць, не дорівнював би нулю.

В нашому випадку маємо три основні одиниці - м, кг, с. З наведеної сукупності параметрів виберемо три - такими параметрами можуть бути m, , F₀. Позначимо розмірності наступним чином: кг - М, м - L, с - Т.

Зробимо заміну розмірностей обраних параметрів m, , F₀ через добуток основних розмірностей у відповідних ступенях:

[m]=[М]¹[L]⁰[Т]⁰; []=[М]⁰[L]⁰[Т]^-1; [F₀]=[М]¹[L]¹[Т]^-2

Складемо визначник за цими ступенями:

.

Число величин, що характеризує цей процес, дорівнює 7-ми, ранг матриці рівний 3-м. Тому число безрозмірних комплексів, які характеризують цей процес, визначається як різниця між загальним числом параметрів і їхньою основною кількістю, тобто кількість безрозмірних комплексів у нашому випадку буде дорівнювати 7-3=4.

Рівняння (1.1) можна також виразити так:

, (3.2)

або у загальному вигляді може бути уявленим як сукупність критеріїв:

. (3.3)

Значення , ,  для кожного з критеріїв знаходяться з умови, що розмірність кожного критерію дорівнює одиниці.

Для першого члена критеріальної функції розмірності, що входять до його величин, записуються наступним чином:

Якщо добуток розмірностей у відповідних ступенях дорівнює одиниці, то припускаємо, що і кожна розмірність також дорівнює 1, тобто , і . З курсу вищої математики відомо, що якщо число, яке зведене у деякий ступінь, дорівнює одиниці, то сама ступінь повинна дорівнювати нулю. Згідно з цим ми можемо з ступіней розмірностей скласти системи з трьох рівнянь:

,

звідки знаходимо _х=1, _х=-1, _х=-2.

Перевірку розмірностей знайденого критерію здійснюємо таким чином:

Згідно за отриманими степенями , ,  критерій ₁ буде мати вигляд:

. (3.4)

Аналогічно знаходимо і інші критерії. Так, для другого члена критеріальної функції розмірності, що містять його величини, можна записати так:

.

, звідки знаходимо _k=0, _k=1, _k=1.

Перевірка розмірностей критерію ₂:

Критерій ₂ буде мати вигляд:

. (3.5)

Для третього члена критеріальної функції розмірності величин записуємо наступним чином:

.

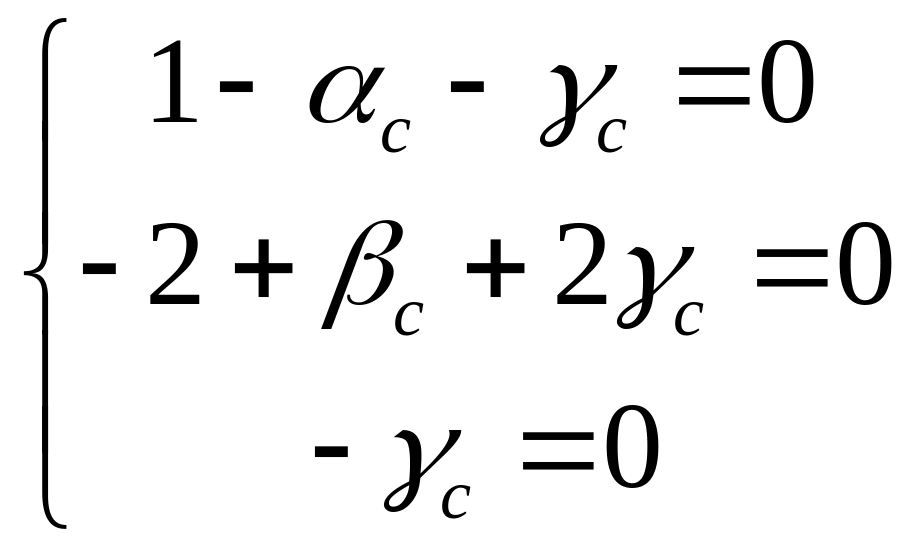, звідки знаходимо _с=0, _с=1, _с=2.

Перевірка розмірностей критерію ₃:

Критерій ₃ буде мати вигляд:

. (3.6)

Розмірності останнього (четвертого) члена критеріальної функції запишемо так:

, звідки знаходимо _t=0, _t=0, _t=-1.

Перевірка розмірностей критерію ₄:

Критерій ₄ буде мати вигляд:

. (3.7)

Рівняння (3.3) з урахуванням виразів (3.4)-(3.7) можна записати у вигляді:

. (3.8)

'

Результати експерименту дозволяють визначити взаємозв'язок між вказаними параметрами, котрий буде справедливим як для моделі, так і для взірця, а математичне формулювання цього зв'язку буде мати вигляд ₁=idem, ₂=idem, ₃=idem, ₄=idem.