2.4. Пошук рішення

Для виконання подальших розрахунків в меню «Сервис» вибираємо команду «Поиск решения». У діалоговому вікні, що з'явиться (рисунок 2.7¹) заповнюємо відповідні поля за такою схемою:

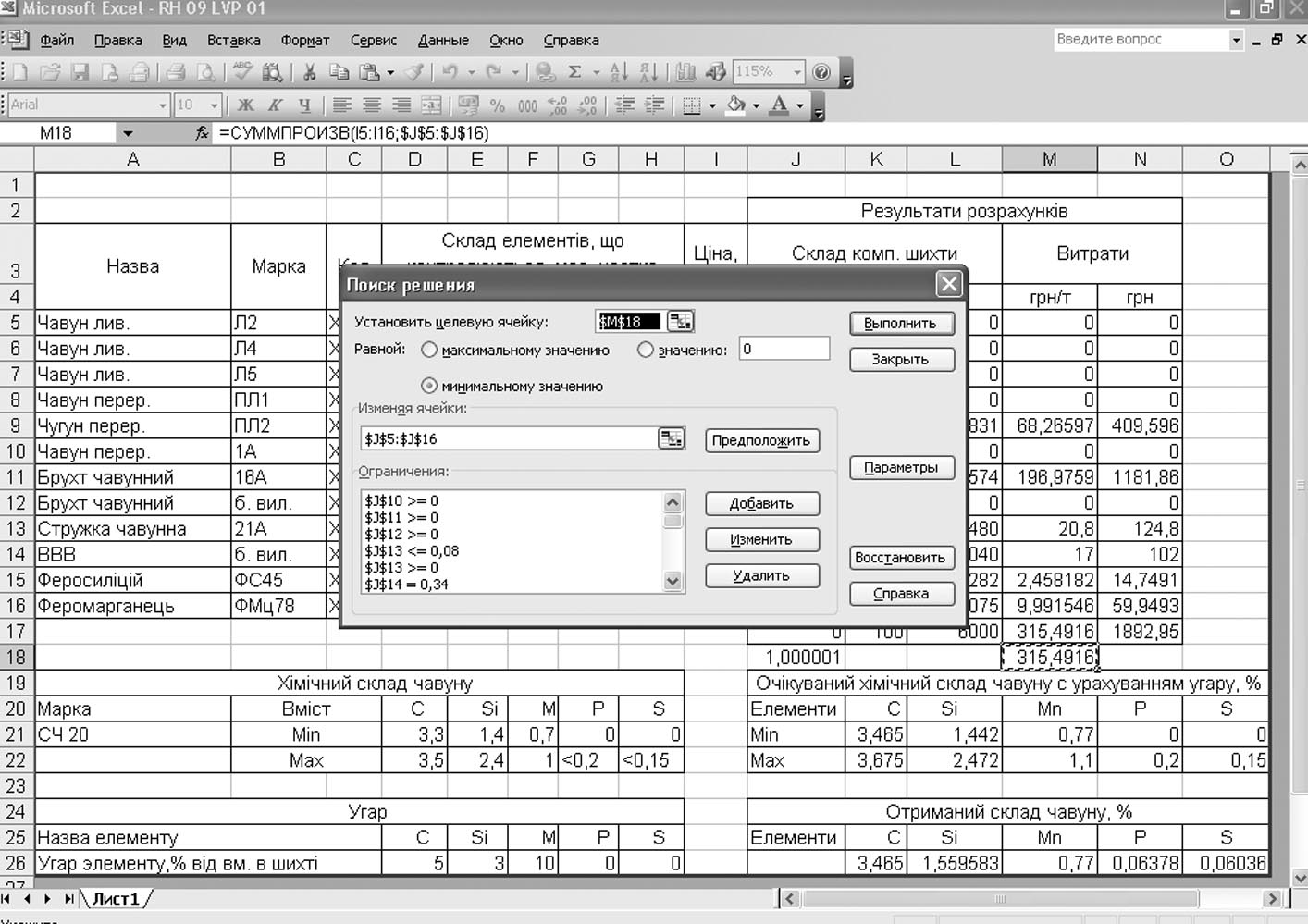
Рисунок 2.7 – Використання пункту «Поиск решения»

«Установить целевую ячейку». Вводимо адресу цільової функції – «целевой ячейки». У нашому випадку це комірка М18. Отже, в це поле вводимо значення $М$18.

«Равной: максимальному значению; значению, минимальному значению». Дане поле визначає тип оптимізації (шукати максимум, мінімум, або конкретне значення функції). Наше завдання визначити склад шихти з мінімальною вартістю, тому ставимо крапку у цьому полі на оцінці - “минимальному значению”.

«Изменяя ячейки». Оскільки ми шукаємо мінімум функції, змінюючи вміст компонентів шихти, які наведені в діапазоні комірок J5-J16, то в дане поле вводимо наступний вираз: $J$5:$J$16.

«Ограничения». У дане поле вводимо лінійні обмеження (2.3)-(2.24). При завданні системи обмежень використовується кнопка «Добавить». При її натисканні з'являється допоміжне діалогове вікно, у поля якого вводяться посилання на комірки й обмеження, що накладаються на змінні в розглянутому завданні. Як видно з рисунку 2.7 , сформовану систему обмежень надалі можна редагувати. Для цього служать кнопки «Изменить» и «Удалить».

Розглянемо докладно кожне обмеження:

Нерівністю (2.3) - обмежується нижня межа вмісту вуглецю в чавуні. Ліва частина нерівності в таблиці Excel наводиться в комірці К26, а права частина нерівності - в комірці К21. Отже, для оформлення обмеження, передбаченого нерівністю (2.3), необхідно зробити наступні дії. У меню «Поиск решения» натискаємо кнопку «Добавить», відкривається меню «Добавление ограничения», у поле «Ссылка на ячейку» уводимо адресу комірки, у якій робиться підсумовування вмісту вуглецю в чавуні, тобто $К$26; у поле математичної операції вводимо знак нерівності >=; в поле «Ограничение» вводимо мінімально допустимий вміст вуглецю в чавуні з урахуванням угару, значення якого розраховано й наведено в комірці $К$21; натискаємо кнопку «Добавить», - обмеження введене.

Нерівність (2.4) - обмежує верхню межу вмісту вуглецю в чавуні. Оформлення обмеження здійснюємо в такій самій послідовності. В меню «Поиск решения» натискаємо кнопку «Добавить», відкривається меню «Добавление ограничения», в поле «Ссылка на ячейку» вводимо адресу комірки, в якій робиться підсумовування вмісту вуглецю в чавуні, тобто $К$26; в поле математичної операції вводимо знак нерівності <=; в поле «Ограничение» вводимо максимально допустимий вміст вуглецю в чавуні з урахуванням угару, значення якого розраховано й наведено в комірці $К$22; натискаємо кнопку «Добавить», - обмеження введене.

Подальші дії по введенню обмежень зрозумілі, тому приводимо тільки конкретні вирази, що уводяться у відповідні комірки.

Нерівність (2.5) - $L$26 >= $L$21.

Нерівність (2.6) - $L$26 <= $L$22.

Нерівність (2.7) - $M$26 >= $М$21.

Нерівність (2.8) - $М$26 <= $М$22.

Нерівність (2.9) - $N$26 <= $N$22.

Нерівність (2.10) - $0$26 <= $0$22.

Рівність (2.11) - визначає суму компонентів шихти, рівну (у відносних одиницях) 1. Підсумовування компонентів шихти робиться в комірці J17. Отже, для оформлення даного обмеження ми повинні ввести у відповідні поля меню «Добавить» обмеження вираз $J$17=1.

Рівність (2.12) - обмежує кількість вороття. Вміст вороття в складі шихти наведено в комірці J14, отже, вводимо вираз $J$14=0,34. Всі наступні нерівності оформляємо по за тією же схемою.

Нерівність (13) - $J$13 >= 0.	Нерівність (19) - $J$9 >= 0.
Нерівність (14) - $J$13 <= 0,08.	Нерівність (20) - $J$10 >= 0.
Нерівність (15) - $J$5 >= 0.	Нерівність (21) - $J$11 >= 0.
Нерівність (16) - $J$6 >= 0.	Нерівність (22) - $J$12 >= 0.
Нерівність (17) - $J$7 >= 0.	Нерівність (23) - $J$15 >= 0.
Нерівність (18) - $J$8 >= 0.	Нерівність (24) - $J$16 >= 0.

Всі передбачені обмеження введені. Тепер можна знайти оптимум функції. Для цього в меню «Поиск решения» натискаємо на кнопку «Выполнить», після чого буде здійснена процедура «Поиск решения», за результатами якої виводиться повідомлення про знайдене рішення (рисунок 2.8).

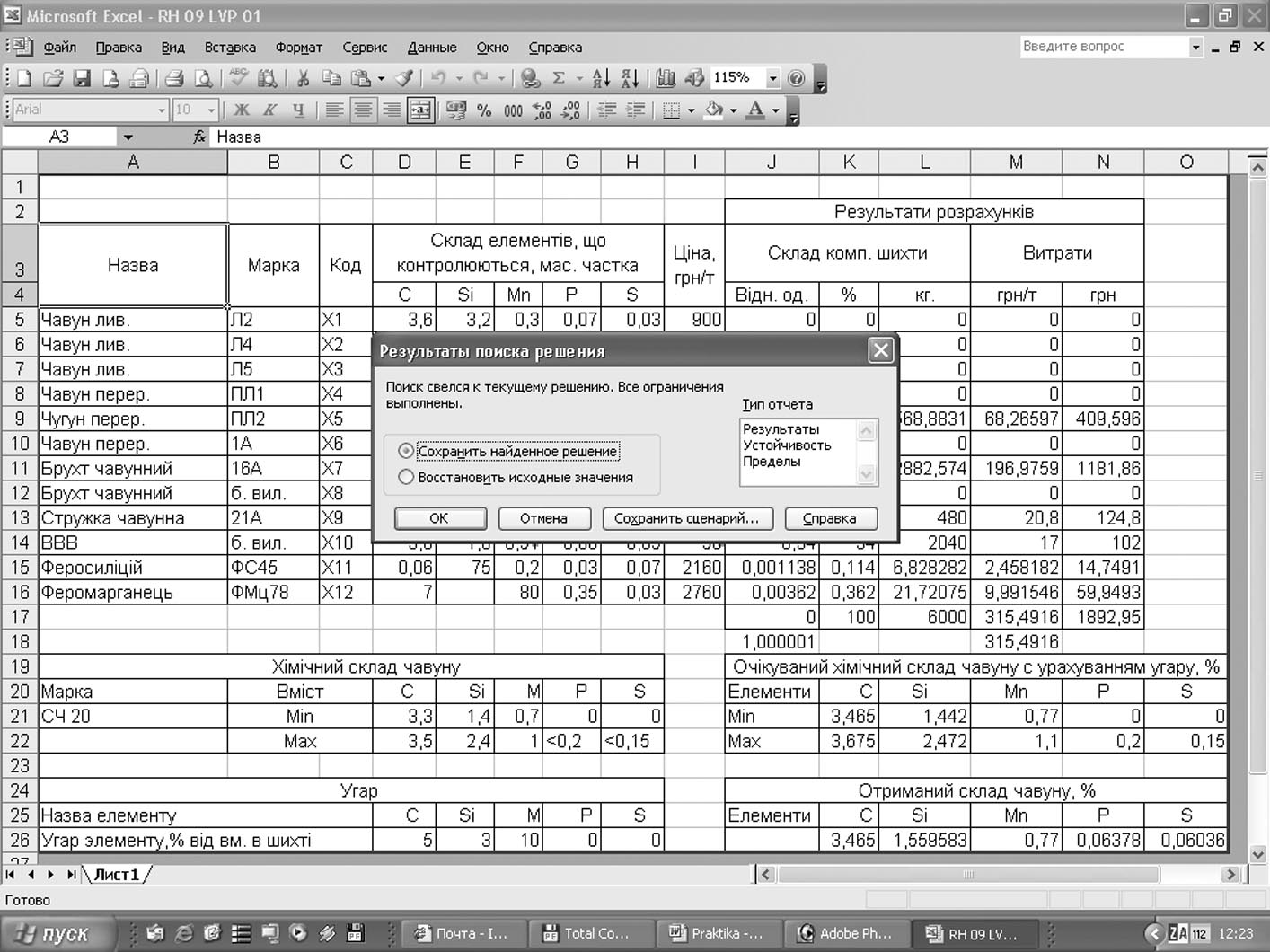
Рисунок 2.8 – Результати пошуку рішень

Як видно з рисунку 2.8, отримані результати можна зберегти (кнопка «ОК»); можна також відмовитися від збереження результатів (кнопка «Отмена»). При виконанні завдання результати необхідно зберегти.

Таким чином, ми одержали шукане рішення, сформульоване завданням оптимізації: з наявних (відповідно до прийнятих умов завдання) 16 компонентів шихти, призначених для одержання сірого чавуну марки СЧ20, програма вибрала склад шихти (у відсотках і кг), що забезпечує мінімальну вартість витрат на його придбання.

Після виконання розрахунків за наведеним прикладом студенти повинні виконати самостійно розрахунки оптимального складу шихти за варіантами, що наведені у наступному пункті.