4.3.4 Метод половинного зворотного кроку

У випадку, коли кінцевий інтервал пошуку мінімуму не заданий, застосовується метод половинного зворотного кроку. Цей метод полягає в русі з деякої початкової точки х₀ з постійним кроком h в напрямку зменшення цільової функції (якщо шукається мінімум) або її збільшення (якщо шукається максимум) до першого невдалого кроку, коли відповідно функція починає зростати або спадати (рис. 4.4). Наступний крок виконується в зворотному напрямку, причому величина кроку приросту зменшується в 2 рази. Так триває до тих пір, доки величина кроку не зрівняється з точністю пошуку мінімуму.

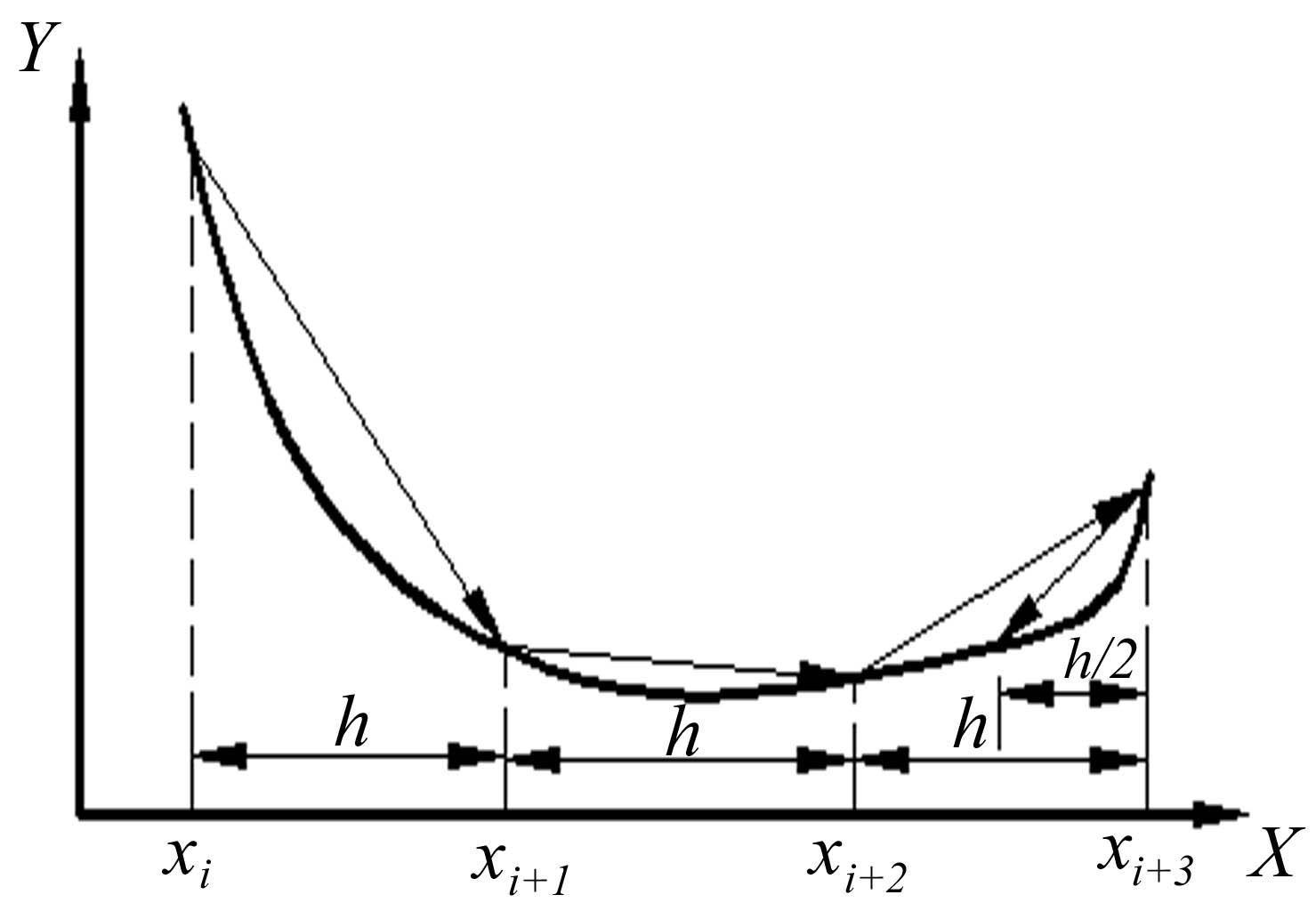
Рис. 4.4 - Схема руху в методі половинного зворотного кроку

Цей метод можна застосовувати і для пошуку мінімуму або максимуму на заданому інтервалі [а, b]. В цьому випадку за початкову точку доцільно обирати ліву границю інтервалу, а за початковий крок - величину . У процесі пошуку необхідно контролювати можливість виходу змінної за межі інтервалу [а, b]. Якщо значення вийшло за межі, то змінну повертають на границю, крок пошуку зменшують вдвічі, а напрямок змінюють на протилежний.

4.4. Вхідні дані до розрахунків

Варіанти 1-5

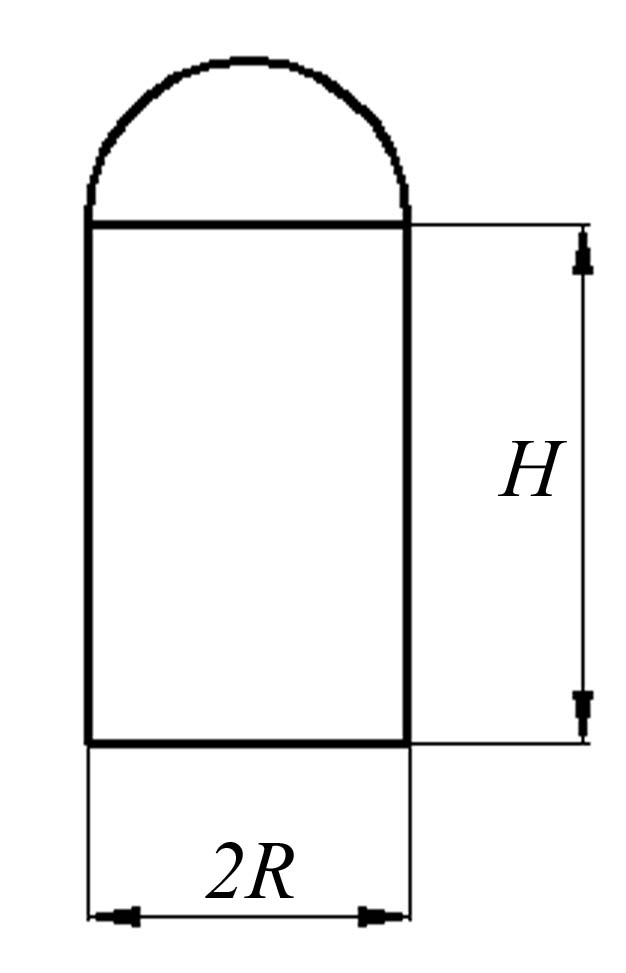
Задача 1. Виливок має форму циліндра з напівсферичним куполом. Об'єм виливка V заданий. Підібрати оптимальні з точки зору витрати матеріалів розміри виливка (площа основи враховується). Похибка розрахунку - в межах 1 см.

Варіант	V, м3	Обмеження, м	Метод рішення
1	60	2,0≤R≤2,5	Дихотомії
2	70	2,2≤R≤2.7	Золотого перетину
3	80	Немає	Половинного зворотного кроку
4	100	2,0≤R≤2,5	Фібоначчі
5	110	2,0≤R≤3,0	Половинного зворотного кроку

Задача 2. В умовах задачі 1 необхідно максимізувати об'єм виливка при заданій площі його поверхні S. Похибка розрахунку така ж.

Варіант	S, м2'	Обмеження, м	Метод рішення
1	70	Немає	Половинного зворотного кроку
2	80	2,1≤R≤2,6	Фібоначчі
3	120	2,0≤R≤2,5	Золотого перетину
4	100	2,5≤R≤3,0	Половинного зворотного кроку
5	140	2,4≤R≤2,6	Дихотомії

Варіанти 6-10

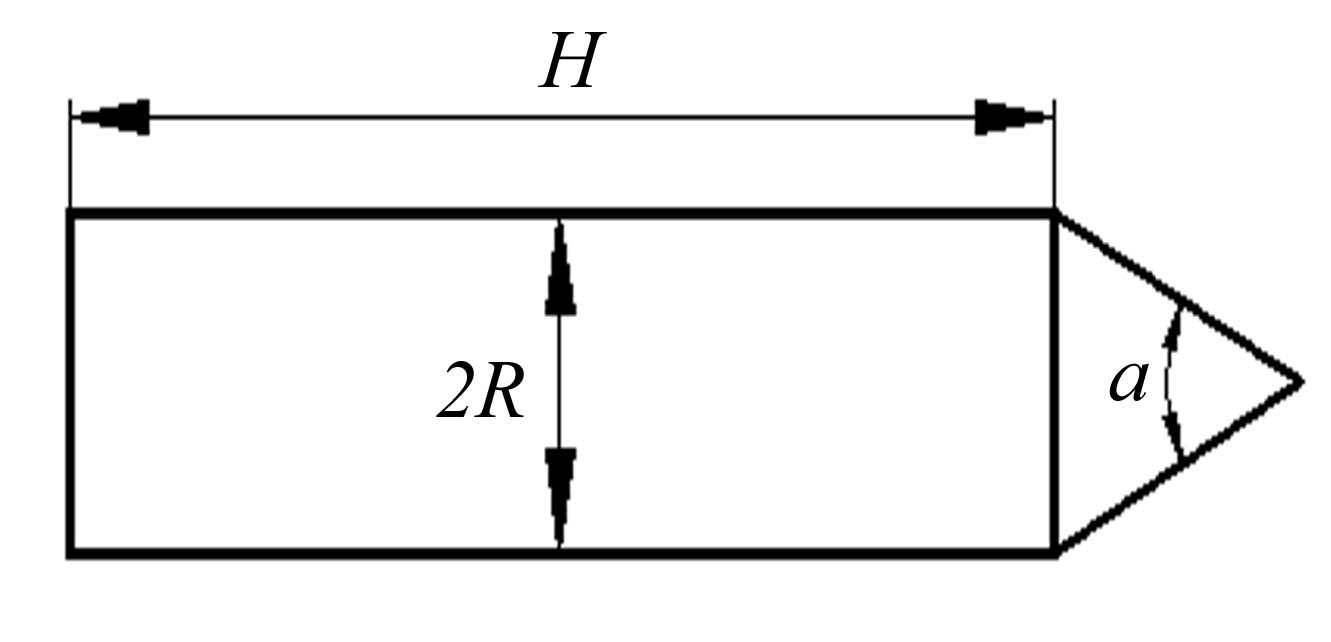
Задача 3. Виливок об'ємом V має форму циліндра з конічним торцем. Кут при вершині конуса =90°. Підібрати з похибкою до 5 мм оптимальні розміри виливка R та Н з точки зору витрати матеріалу на його виготовлення.

Варіант	V,м3	Обмеження, м	Метод рішення
6	3,0	0,7≤R≤1,0	Золотого перетину
7	3,5	Немає	Половинного зворотного кроку
8	4,0	0,8≤R≤1,1	Дихотомії
9	5,0	0,6≤R≤0,9	Половинного зворотного кроку
10	6,0	0,9≤R≤1,2	Фібоначчі

Задача 4. В умовах задачі 3 підібрати розміри виливка, що забезпечать його максимальний об'єм при фіксованій вазі (тобто при заданій площі поверхні S).

Варіант	S, м2	Обмеження, м	Метод рішення
6	10,0	0,6≤R≤0,9	Фібоначчі
7	15,0	0,6≤R≤1,2	Дихотомії
8	20,0	1,1≤R≤1,4	Золотого перетину
9	22,5	Немає	Половинного зворотного кроку
10	25,0	1,2≤R≤1,5	Половинного зворотного кроку

Варіанти 11-15

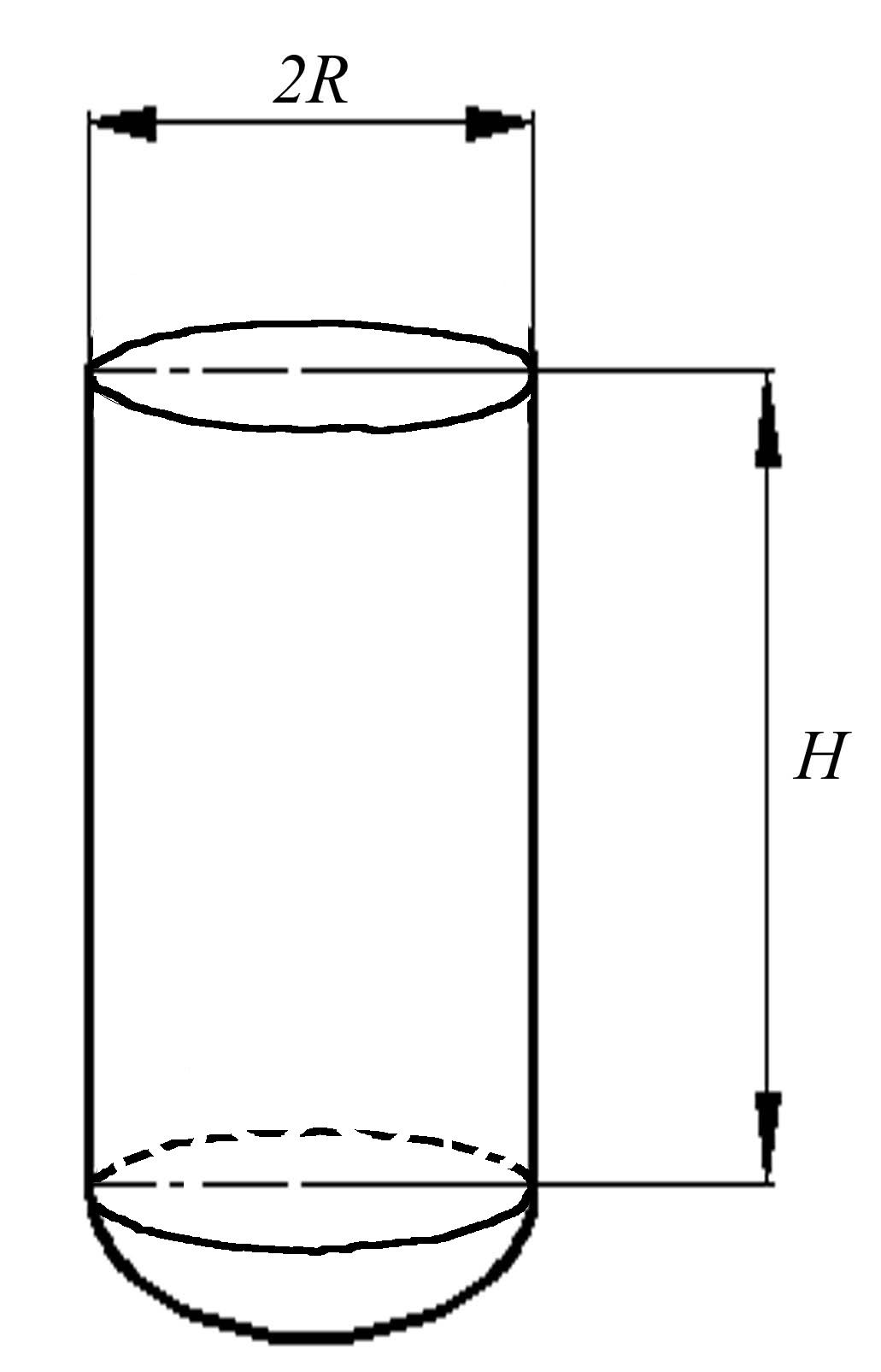
Задача 5. Спроектувати замкнуту тонкостінну ємність, яка має при заданому об'ємі V мінімальну масу, (тобто мінімальну площу поверхні). Ємність є сукупністю циліндричної поверхні та двох напівсферичних поверхонь. Похибка отримання параметрів Н і R - 5 мм.

Варіант	V, м3	Обмеження, м	Метод рішення
11	2,0	0,3≤R≤0,5	Половинного зворотного кроку
12	3,0	0,4≤R≤0,6	Фібоначчі
13	3,5	Немає	Половинного зворотного кроку
14	3,5	0,15≤R≤0,65	Дихотомії
15	4,0	0,5≤R≤0,7	Золотого перетину

Задача 6. В умовах задачі 5 підібрати розміри R і Н так, щоб при заданій масі (тобто площі поверхні S) ємність мала найбільший об'єм.

Варіант	S, м2	Обмеження, м	Метод рішення
11	8	0,3≤R≤0,5	Фібоначчі
12	10	0,35≤R≤0,55	Половинного зворотного кроку
13	12	0,4≤R≤0,6	Золотого перетину
14	14	Немає	Половинного зворотного кроку
15	16	0,6≤R≤0,8	Дихотомії

Варіанти 16-20

Задача 7. Cпроектувати бак у вигляді циліндра з конічними заднім та переднім днищем. Об'єм бака повинен складати V. Підібрати з похибкою до 5 мм таки розміри R і Н, щоб на виготовлення бака було витрачено мінімум матеріалу (=90°).

Варіант	V, м3	Обмеження, м	Метод рішення
16	2.0	0,6≤R≤0,8	Половинного зворотного кроку
17	2,5	Немає	Половинного зворотного кроку
18	4,0	0,8≤R≤1,0	Золотого перетину
19	5,0	0,9≤R≤1,1	Дихотомії
20	6,0	1,0≤R≤1,2	Фібоначчі

Задача 8. В умовах задачі 7 підібрати розміри бака, що забезпечують максимальну його місткість при фіксованій вазі (тобто при заданій площі поверхні S).

Варіант	S, м2	Обмеження, м	Метод рішення
16	10	0,8≤R≤1,0	Золотого перетину
17	15	0,9≤R≤1,1	Фібоначчі
18	20	1,0<К<1,2	Половинного зворотного кроку
19	28	Немає	Половинного зворотного кроку
20	30	1,3≤R≤1,5	Дихотомії

Варіанти 21-25

Задача 9. Резервуар утворений циліндричною та напівсферичною поверхнями. Підібрати з похибкою до 1 см такі розміри R і Н, які б забезпечували мінімум витрат матеріалу на виготовлення резервуара при заданій його місткості V. Вважати, що кришки резервуар не має.

Варіант	V, м3	Обмеження, м	Метод рішення
21	5	0,8≤R≤1,2	Фібоначчі
22	10	1,0≤R≤1,3	Половинного зворотного кроку
23	15	1,3≤R≤1,6	Дихотомії
24	20	Немає	Половинного зворотного кроку
25	25	1,9≤R≤2,1	Золотого перетину

Задача 10. В умовах задачі 9 підібрати розміри R і Н, щоб при заданій площі поверхні місткість резервуара була максимальною.

Варіант	S, м2	Обмеження, м	Метод рішення
21	15	0,9≤R≤1,2	Золотого перетину
22	20	1,1≤R≤<1,4	Половинного зворотного кроку
23	25	1,3≤R≤1,6	Дихотомії
24	30	1,5≤R≤1,8	Фібоначчі
25	35	Немає -	Половинного зворотного кроку

Звіт про виконання практичного заняття 2 повинен мати для кожного з завдань:

1. Умову завдання.

2. Математичне формулювання задач оптимізації.

3. Друковану версію програми розрахунків, виконану на будь-якій алгоритмічній мові.

4. Результати розрахунків.