4.3.2 Метод золотого перетину

Метод золотого перетину є розвитком методу дихотомії. В цьому методі значення х_1,i, та х_2,і на і-ому кроку розташовуються також симетрично відносно центру інтервалу неозначеності, але з урахуванням коефіцієнту пропорційності :

, . (4.4)

Після цього в цих точках вираховуються значення цільової функції F(х), аналізуються умови (4.2) і пошук триває. Ірраціональне число характеризує так званий золотий перетин. Його особливість полягає в тому, що

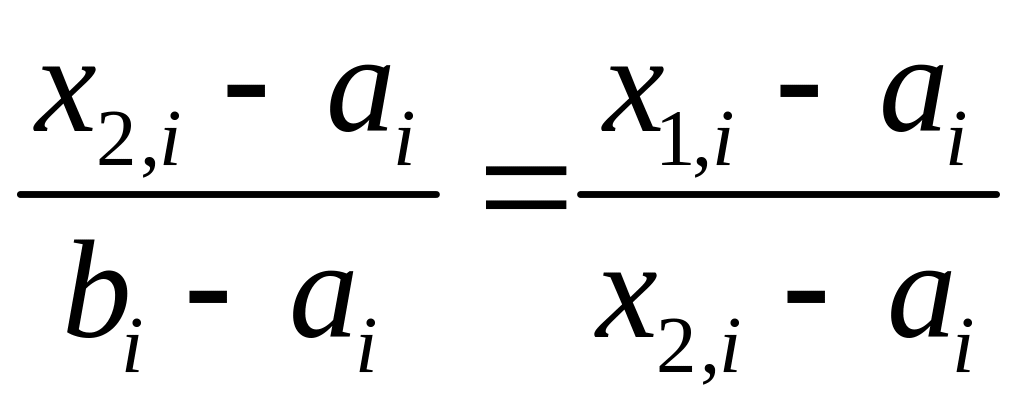; . (4.5)

Тобто точка х_1,i ділить в тому же відношенні відрізок [а_i, х_2,і], що і точка х_2,i відрізок [а_i, b_i], а точка х_2,i - відрізок [x_1,i, b_1,i] в тому же підношенні, що і точка x_1,i, відрізок [а_i, b_i]. У зв'язку з цим при розбитті нового інтервалу неозначеності [а_i+1, b_i+1], за формулами (4.4) одна з внутрішніх точок і значення функції в ній вже відомі, тому на кожній новій ітерації значення цільової функції доводиться вираховувати тільки один раз.

Для спрощення реалізації методу золотого перетину другу з умов (4.2) можна віднести до першої, тобто для звуження інтервалу неозначеності і його наступного ділення слід використати співвідношення:

якщо F(x_1,i)≤F(x_2,i), тоді а_i+1=а_і, b_і+1=х_2,і; x_2,i+1=x_1,I;

якщо F(x_1,i)>F(x_2,i), тоді а_i+1=x_1,i, b_і+1=b_і. x_1,i+1=x_2,I. (4.6)

Значення точки розбиття х_1,і+1, або х_2,і+1, якого не вистачає, вираховується за однією з формул (4.4). Обчислення за формулами (2.4) і (2.6) припиняються, як тільки межі інтервалу, що містить точку мінімуму, стануть відрізнятися один від одного менш ніж .

При використанні методу золотого перетину довжина інтервалу неозначеності на кожному кроку зменшується лише у рази, але при цьому доводиться вираховувати значення цільової функції тільки в одній точці. Тому метод золотого перетину, в цілому, ефективніший за метод дихотомії.

2.3.3 Метод Фібоначчі

Метод Фібоначчі заснований на використанні так званих чисел Фібоначчі, тобто послідовності чисел, яка будується за наступним правилом:

₁, =1; ₂ =1; _i=_i-1+_i-2, і=3,4,...,n. (4.7)

Характерна особливість чисел Фібоначчі - рівність чергового члена послідовності сумі двох попередніх. У цьому методі спочатку, виходячи зі значення точності , визначається _n - найменше з чисел Фібоначчі, що задовольняє умові

, (4.8)

де [а₀, b₀] - початковий інтервал неозначеності. Також стане відомим номер n останнього числа Фібоначчі.

Позначимо 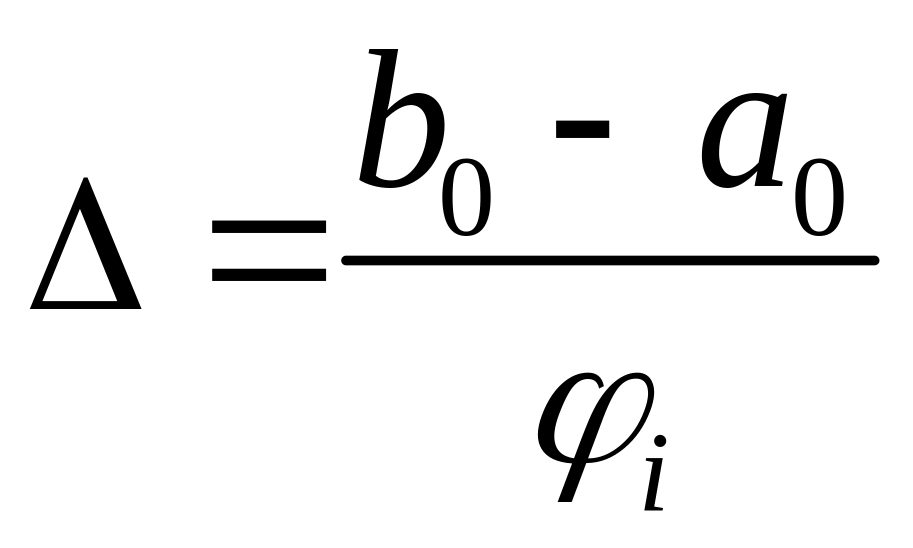. Тоді , тобто весь інтервал неозначеності [а₀, b₀] можна розбити на кількість частин, яка дорівнює _n, причому довжина кожної частини  буде менша за . За властивістю чисел Фібоначчі

Отже, інтервал [а₀, b₀] можна розбити на три частини з довжинами , , .

Точки ділення x_1,0 та х_2,0 визначаються так:

. (4.9)

Порівнюючи значення цільової функції в точках x_1,0 та х_2,0, знаходимо новий інтервал неозначеності [а₁, b₁] (на рис. 4.3 показаний випадок, коли F(x_1,0)F(x_2,0).

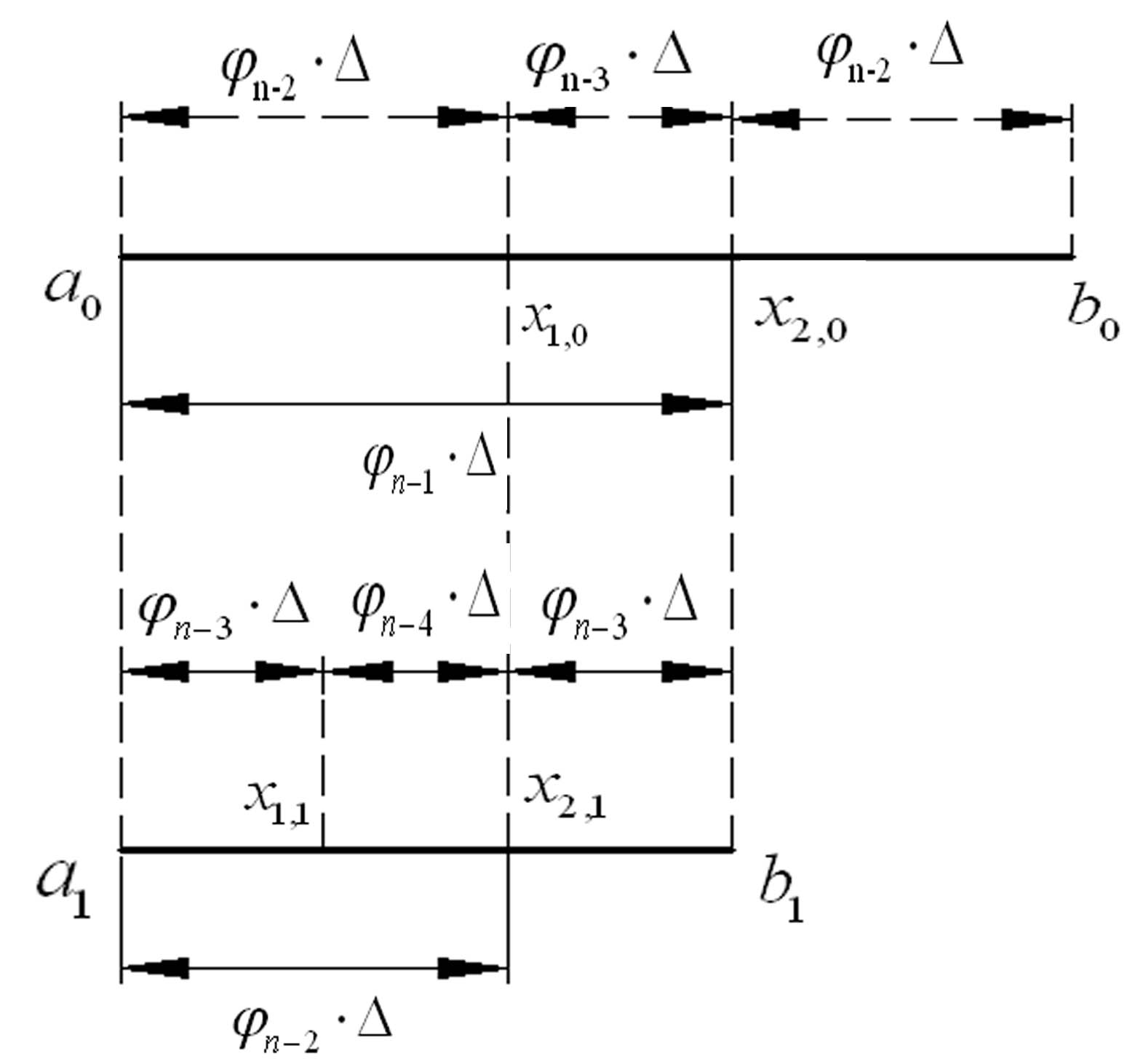
Рис. 4.3 - Схема ділення відрізків у методі Фібоначчі

Новий інтервал, довжина якого , припускає точно таке ж ділення на три відрізки довжинами , , . Причому одна точка ділення та значення функції в ній відомі (х_2,i=х_1,0), а друга визначається аналогічно виразам (4.9):

.

В загальному випадку на і-ому кроку (і=0,1,2,...) перевіряється значення цільової функції в точках х_1,i, i х_2,i та у відповідності з співвідношеннями (4.6) вибираються межі нового інтервалу неозначеності і одна з точок ділення. Друга точка ділення знаходиться за однією з наступних формул:

; . (4.10)

Значення цільової функції на кожному кроку (крім нульового) вираховується тільки один раз. Кількість ітерацій в методі Фібоначчі фіксовано і дорівнює n-4, де n вираховується заздалегідь, як було сказано раніше, за допомогою умови (4.8). На останньому (n-4)-ому кроку довжина інтервалу буде , а точки розбиття поділять його на три відрізки довжиною . Таким чином, точка мінімуму визначиться з похибкою ≤, а для досягнення цієї точності буде потрібно (n-2) обчислень функцій.

Швидкість сходження методу Фібоначчі трохи вища, ніж методу золотого перетину. Вважається, що метод Фібоначчі оптимальний, якщо ставиться завдання досягнення найкращої точності за визначену кількість кроків. В той же час слід пам'ятати, що в цьому методі до початку знаходження мінімуму функції за стандартною методикою необхідно визначити самі числа Фібоначчі і задати число обчислень функцій. Тим самим його переваги у порівнянні з методом золотого перетину значно зменшуються.