4.3 Опис чисельних методів одновимірної оптимізації

Розглянемо випадок, коли цільова функція F(х) залежить тільки від одного проектного параметру х. Такі задачі цікаві самі по собі, тому що часто зустрічаються в процесах проектування та, крім того, до таких задач зводяться набагато складніші задачі багатовимірної оптимізації.

Як було показано раніше, процес оптимізації - це процес пошуку тих значень параметру х, при яких функція F(х) має максимум або мінімум. В подальшому під задачею оптимізації будемо розуміти задачу знаходження мінімуму функції F(х). Це ні в яком разі не зменшує спорідненість розглядуваних методів, тому що задача знаходження максимуму функції F(х) елементарно зводиться до задачі пошуку мінімуму функцій F(х). Крім того, будемо припускати, що функція унімодальна, тобто має тільки один екстремум на розглядуваному інтервалі. В протилежному випадку, перш ніж приступити до знаходження екстремумів, необхідно їх локалізувати, тобто виділити ті інтервали, всередині яких знаходиться тільки один екстремум. Оскільки точне значення екстремуму при цьому невідомо, то інтервал, на якому він знаходиться, будемо називати інтервалом неозначеності.

Отже, задача оптимізації на даному етапі зводиться ось до такого: на інтервалі неозначеності [а, b] потрібно знайти значення аргументу х, що відповідає мінімуму функції F(х). Загальний принцип розглянутих далі методів пошуку екстремуму полягає в тому, що на кожному кроку послідовно звужуються межі інтервалу неозначеності. Це значить, що за заданим інтервалом [а, b], що містить х, визначається новий інтервал [а_i+1, b_i+1], який також містить х, причому

Від кроку до кроку інтервал стає все вужчим, поки його довжина не стане менше певного заданого числа  - точності обчислення мінімуму. Будь-яка з внутрішніх точок останнього інтервалу може бути прийнята за значення х, причому похибка обчисленого значення буде не більша за . В кожному конкретному методі наведена умова закінчення розрахунку може бути уточнена.

В залежності від стратегії визначення нових меж інтервалу неозначеності розрізняють ряд методів пошуку мінімуму, найбільш відомими х яких є способи дихотомії, золотого перетину і Фібоначчі. Часто застосовують також різноманітні комбінації методів, наприклад, комбінацію методу золотого перетину і послідовної параболічної інтерполяції.

4.3.1 Метод дихотомії

Метод дихотомії - один з самих простих способів пошуку екстремуму. Згідно йому на і-ому кроку вираховуються два значення: х_{1, i}, та х_{2, i}, на відстані /2 праворуч і ліворуч від середини інтервалу неозначеності, тобто

(4.1)

де а_і, b_і - межі інтервалу неозначеності на і-ому кроку;  - точність визначення х, яка задана.

Обчисливши F(x_1,i) та F(x_2,i) і порівнявши отримані значення (рис. 4.2), знайдемо новий інтервал неозначеності:

якщо F(x_1,i)<F(x_2,i), тоді а_i+1=а_і, b_і+1=х_2,і;

якщо F(x_1,i)=F(x_2,i), тоді а_i+1=x_1,i, b_і+1=х_2,і; (4.2)

якщо F(x_1,i)>F(x_2,i), тоді а_i+1=x_1,i, b_і+1=b_і.

В новому інтервалі неозначеності знову визначаємо координати х_1,і і х_2,і та продовжуємо пошук до тих пір, доки довжина інтервалу неозначеності не стане менше 2, тобто доки не виконається умова:

. (4.3)

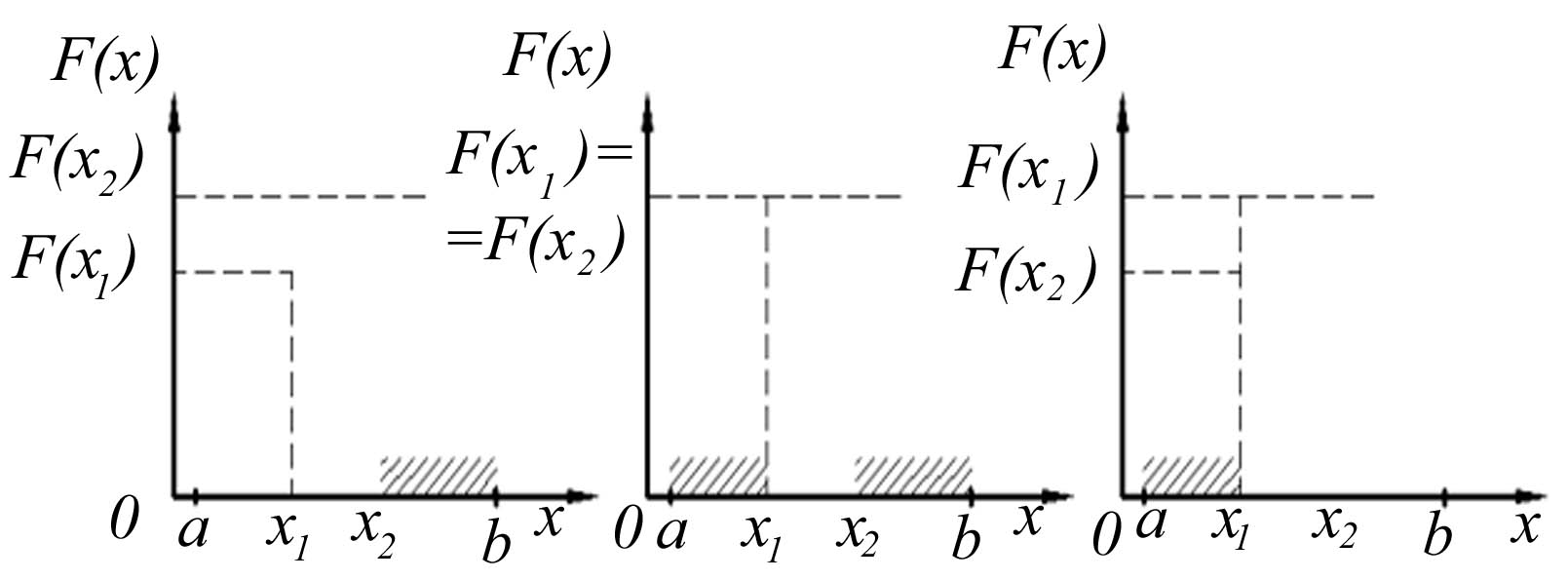
Рис. 4.2 - Визначення області подальшого пошуку (заштрихована область відкидається)

Точкою мінімуму буде та з точок х_1,i, або х_2,і, значення функції в якій менше. Похибка обчислення мінімуму при цьому не перевищує . При достатньо малому  на кожному кроку довжина інтервалу неозначеності зменшується приблизно в 2 рази; для виконання і-го кроку необхідно обчислити значення цільової функції F(x) в двох точках.