2. Решение задач с2

Пример 1.

В прямоугольном параллелепипеде АВСDA1B1C1D1 известны длинны ребер:

AB = 3; AD = 4; CC1 = 4. Найдите угол между плоскостями BDD и ADB (задание С2 из ЕГЭ 2010 г.)

Решение.

Введем в пространстве систему координат С1xyz. Запишем координаты точек:

В1 (0; -4; 0), В (0; -4; 4), А (3; -4; 4), D1 (3; 0; 0), D (3; 0; 4). Составляем уравнения плоскости с помощью формулы Ах+Ву+Сz+D=0.

Для плоскости ВDD1

Ӏӏӏ . Использование метода координат в с4

3.1. Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат   и  . Оси координат пересекаются в точке  , которая называется началом координат, на каждой оси выбрано положительное направление.

Положение точки   на плоскости определяется двумя координатами   и  . Координата   равна длине отрезка  , координата   — длине отрезка   в выбранных единицах измерения. Отрезки   и   определяются линиями, проведёнными из точки  параллельно осям   и   соответственно.

При этом координате   приписывается знак минус, если точка   лежит на луче   (а не на луче  , как на рисунке). Координате   приписывается знак минус, если точка   лежит на луче  . Таким образом,  и   являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Координата   называется абсциссой точки  ,

координата  ординатой точки  .

Символически это записывают так:

или

или указывают принадлежность координат конкретной точке с помощью индекса:

и тд.

В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси   вверх, ось   смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно - например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).Четыре угла (I, II, III, IV), образованные осями координат   и  , называются координатными углами или квадрантами. Если точка   лежит в координатном углу I, то точка   имеет положительные абсциссу и ординату. Если точка   лежит в координатном углу II, то точка   имеет отрицательную абсциссу и положительную ординату. Если точка   лежит в координатном углу III, то точка   имеет отрицательные абсциссу и ординату. Если точка   лежит в координатном углу IV, то точка   имеет положительную абсциссу и отрицательную ординату.

Формулы при решении С4

Расстояние от точки A (x₀; y₀) до оси OX равно |y₀|.

Расстояние от точки A (x₀; y₀) до оси OY равно |x₀|.

Расстояние от точки 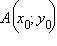  до начала координат равно 

Расстояние |AB| между точками A (x₁; y₁) и B (x₂; y₂) равно 

Точка M, которая является серединой отрезка AB, где A (x₁; y₁) и B (x₂; y₂), имеет координаты 

Координаты середины отрезка

3.2. Решение задач

Задача

Заканчивая представление своей реферативной работы, которой я занималась в течение последних месяцев, хочу сказать.

Конечно, эту работу нельзя считать авторитетным пособием по решению заданий С2 и С4 ЕГЭ по матиматике, так как в ней рассмотрено лишь небольшое количество задач, и ограниченное количество приёмов. Но эта работа является результатом моих дополнительных занятий математикой, поисков литературы, задач, составления слайдов.

Почему же именно эта тема заинтересовала меня?

Как вам известно, я учусь в 11 классе и по окончании школы хочу поступить в престижный вуз. А для этого необходимы высокие баллы ЕГЭ. Я и самостоятельно, и с помощью учителя решала множество заданий уровня С, изучала редко используемые формулы и приёмы, упрощающие решение задач. Координатно-векторный метод решения был для меня открытием. Те задачи, над которыми я ломала голову несколько часов, решались за несколько минут! И мне захотелось поделиться своими знаниями с такими же выпускниками, как и я. Итог этого порыва вы видите перед собой.

Конечно, я не настаиваю на том, что все задачи стереометрии надо решать методом координат, иногда это просто нецелесообразно. Но согласитесь, настолько простое и изящное решение не только освободит время для решения других заданий, но и будет высоко оцениваться проверяющим учителем.