2. Из истории метода координат

Мы уже знакомы с координатами на прямой и на плоскости. Введение координат позволяет определить положение точки с помощью чисел – координат этой точки.

Идея координат зародилась в науке Вавилона и Греции в связи с потребностью географии, астрономии и мореплавания. Ещё во II в. до н.э. греческий учёный Гиппарх предложил определить положение точки на земной поверхности с помощью географических координат – широты и долготы, выражаемых числами.

В XIY в. француз Оремс ( 1323 – 1382) перенёс эту идею в математику. Предложив покрывать плоскость прямоугольной сеткой и называть широтой долготой числа, характеризующие положение точки на этой сетке. Наконец, в XIX в. французский учёный Рене Декарт первым увидел возможность записи геометрических фигур с помощью уравнений, связывающих координаты точек этих линий.

Работа М. Эшера отражает идею введения прямоугольной системы координат в пространстве.

Ӏӏ. Использование метода координат в с2

2.1. Теория при решении с2

Метод координат — это довольно лёгкий способ, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный отрезок и направление осей  x, y и z. Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.

Проанализировав различные геометрические задачи, в том числе задания из ЕГЭ я сделала вывод, что при решении геометрических задач координатным методом постоянно приходится опираться на несколько совсем простых стандартных задач: определение расстояния между точками, отыскание середины отрезка и др. Я смогла сделать вывод об основах метода координат, которые необходимы для решения многих задач уровня С2 Егэ по математике. В таких задачах обычно требуется найти угол между прямыми, или между плоскостями, или между прямой о плоскостью, а также расстояние между аналогичными объектами. Для этого удобно использовать векторы и система координат.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат  ,   и  . Оси координат пересекаются в точке  , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей.   — ось абсцисс,   — ось ординат,   — ось аппликат.

Положение точки   в пространстве определяется тремя координатами  ,   и  . Координата   равна длине отрезка  , координата   — длине отрезка  , координата   — длине отрезка   в выбранных единицах измерения. Отрезки  ,  и   определяются плоскостями, проведёнными из точки   параллельно плоскостям  ,   и  соответственно.

Координата   называется абсциссой точки  ,

координата   — ординатой точки  ,

координата   — аппликатой точки  .

Символически это записывают так:

или

или привязывают запись координат к конкретной точке с помощью индекса:

Прямоугольные все системы координат в трехмерном пространстве делятся на два класса— правые (также используются термины положительные, стандартные) и  левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений.. Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта и тп (положительное направление осей выбирают так, чтобы при повороте оси   против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси  , если этот поворот наблюдать со стороны положительного направления оси  ).

Формулы для решения методом координат:

1. Нахождение расстояния между двумя точками, заданными своими координатами.

гдеd=AB, A(x₁; y₁; z₁), B(x₂; y₂; z₂)

2. Нахождение координаты середины С(x; y; z)отрезка АВ, A(x₁; y₁; z₁), B(x₂; y₂.z₂)

. , ,

3 . Нахождение косинуса, а, следовательно, и самого угла, между двумя векторами, заданными своими координатами.

где .

4. Нахождение угла между плоскостями путем составления уравнения каждой плоскости. Ах+Ву+Сz+D=0 и определения угла между нормалями к плоскостям. Нормаль n при этом имеет координаты .

5.Нахождение расстояния от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно.

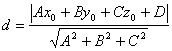
6. Координаты x, y, z точки М, которая делит отрезок , ограниченный точками ( , , ) и ( , , ), в отношении , определяется по формулам

, , .