3.1.2 Пример решения задачи д1.

Механическая система состоит из грузов D₁ массой m₁ и D₂ массой m₂ и из прямоугольной вертикальной плиты массой m₃, движущийся вдоль горизонтальных направляющих ( рис. Д1). В момент времени t₀ =0 , когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r и R по законам и .

Д а н о : m₁ =6 кг, m₂ =8 кг, m₃ =12 кг, r=0,6 м, R=1,2 м, рад, рад ( t-в секундах). О п р е д е л и т ь: - закон движения плиты, - закон изменения со временем полной нормальной реакции направляющих.

Решение. Рассмотрим механическую систему , состоящую из плиты и грузов D₁ и D₂ , в произвольном положении ( рис. Д 1). Изобразим действующие на систему внешние силы : силы тяжести Р₁, Р₂ , Р₃ и реакцию направляющих N. Проведем координатные оси Оху так, чтобы ось у проходила через точку С₃₀ , где находится центр масс плиты в момент времени t₀ =0.

а) Определения перемещения х₃ . Для определения воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось х.

Получим

или (1)

так как , поскольку все действующие на систему внешние силы вертикальны.

Проинтегрировав уравнение (1), найдем, что , т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени , то С₁=0.

Интегрируя уравнение , получим

(2)

т.е. центр масс системы вдоль оси Ох перемещаться не будет.

Определим значение . Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно , . Так как по формуле, определяющей координату х_с центра масс системы, , то

. (3)

В соответствии с равенством (2) координаты центра масс х_с всей системы в начальном и произвольном положении будут равны. Следовательно, учитывая, что при , получим

(4)

Отсюда получаем зависимость от времени координаты х_с.

О т в е т : м, где t –в секундах.

б) Определение реакции N. Для определения составим дифференциальное уравнение движения центра масс системы в проекции на вертикальную ось у ( см. рис. Д 1):

. (1)

Отсюда получим, учтя, что , и.т.д.:

. (2)

По формуле определяющей ординату у_с центра масс системы,

получим

или .

Продифференцировав обе части этого равенства два раза по времени, найдем

;

.

Подставив это значение в уравнение (2), определим искомую зависимость N от t.

О т в е т: , где t –в секундах, N – в ньютонах.

3.2. Теорема об изменении количества движения механической системы.

Количеством движения механической системы называется вектор, равный геометрической сумме ( главному вектору) количеств движения всех материальных точек этой системы.

(1)

Вектор количества движения механической системы имеет модуль, равный произведению массы системы на скорость ее центра масс и направление этой скорости.

Проецируем вектор на оси координат:

: ; (2)

Проекция количества движения механической системы на каждую координатную ось, равная сумме проекций количеств движения всех точек системы на одну ос , определяется произведением массы системы на проекцию скорости центра масс на эту же ось.

Дифференцируем (1) по времени:

.

Согласно уравнению движения центра масс системы,

.

Следовательно, (3)

Уравнение (3) выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил , действующих на эту систему.

Векторному уравнению (3) соответствуют три уравнения в проекциях оси координат:

; : (4)

Уравнения (4) показывают, что производная по времени от проекции количества движения механической системы на любую ось равна проекции главного вектора внешних сил , действующих на систему, на ту же ось.

Из уравнений (3) и (4) следует, что изменение количества движения механической системы вызывается только внешними силами.

С л е д с т в и я и з т е о р е м ы ;

1. Если главный вектор внешних сил за рассматриваемой промежуток времени равен нулю, то количество движения механической системы постоянно.

Из уравнения ( 3) следует, что если

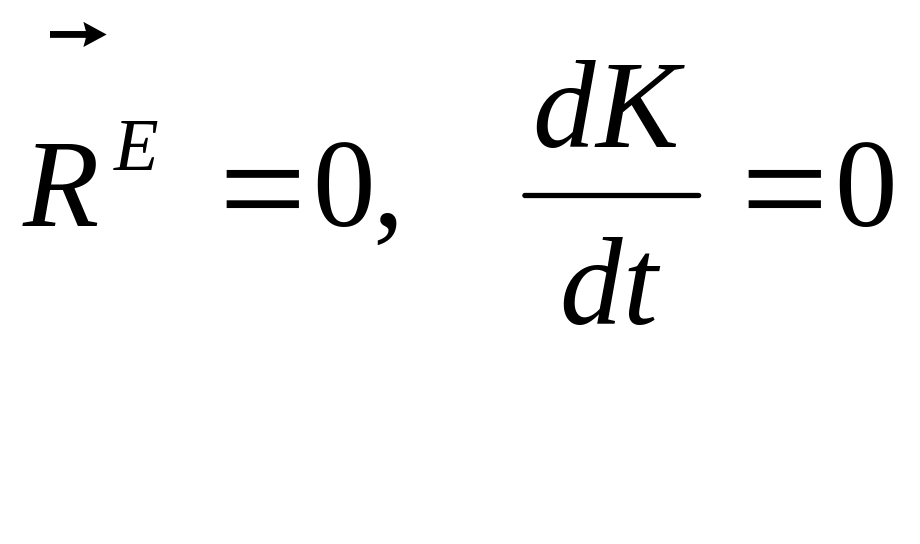
т.е. . (5)

2. Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна.

Так , например, при из первого уравнения (4)

откуда

Следствия из теорем об изменении количества движения механической системы выражают закон сохранения количества движения системы.