Глава 3. Динамика

3.1. Теорема о движении центра масс.

(1)

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору внешних сил.

Уравнение (1) выражает теорему о движении центра масс системы, которая формулируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы , действующие на систему.

Проецируя обе части векторного равенства ( 1) на оси получаем три уравнения в проекциях на оси координат:

; ; (2)

где - проекции силы - проекции главного вектора сил на оси координат. Уравнения (2) представляют собой дифференциальные уравнения движения центра масс. Из уравнений (1) и (2) следует, что внутренние силы непосредственно не влияют на движение центра масс.

С л е д с т в и я из теоремы:

1.Если главный вектор внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Из уравнения (1) следует, что если . При этом если начальная скорость центра масс равна нулю, то центр масс находится в покое. Если же начальная скорость , то центр масс движется прямолинейно и равномерно с этой скоростью.

2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось остается се время равной нулю , то проекция центра масс механической системы на эту ось или неподвижна, или движется равномерно.

Из первого уравнения (2) следует, что если X^E=0, то

Если при этом в начальный момент , то

т.е. координата х центра масс остается постоянной, а при проекция центра масс на ось х движется равномерно.

Следствия из теоремы о движении центра масс системы выражает закон сохранения движения центра масс системы.

3.1.1 Задача д1

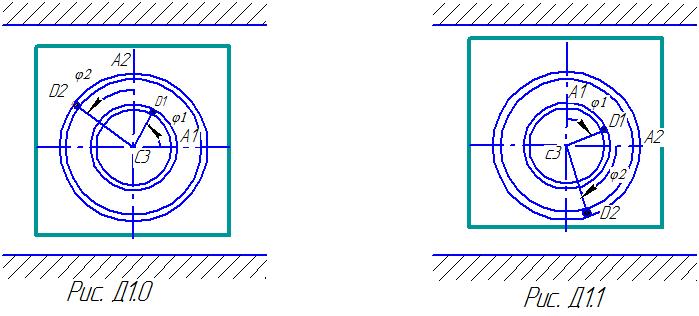
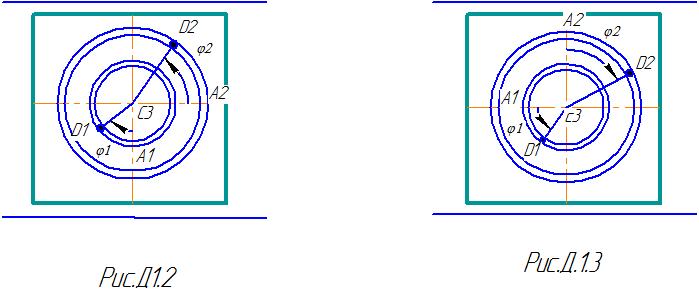
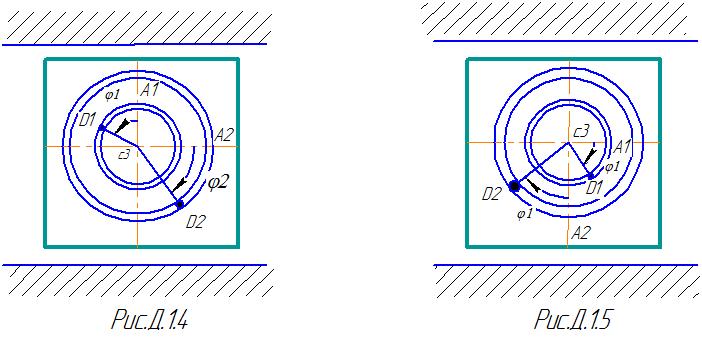
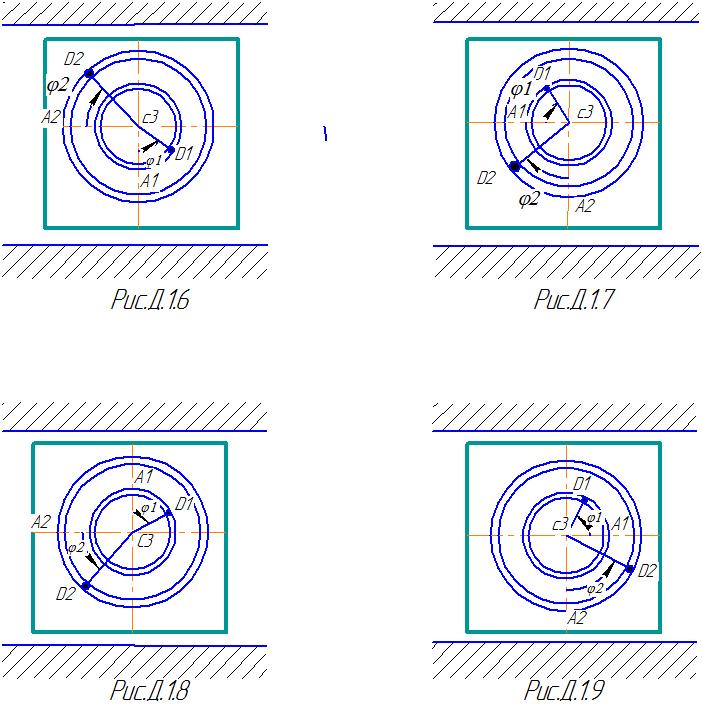
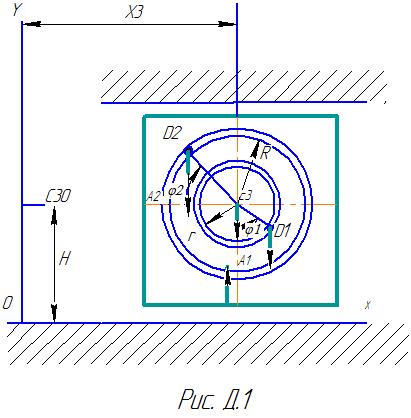
Механическая система состоит из грузов D₁ массой m₁=2 кг, D₂ массой m₂=6 кг и из прямоугольной вертикальной плиты массой m₃=12 кг, движущийся вдоль горизонтальных направляющих (рис. Д.1.0-Д.1.9, табл. Д1). В момент времени t₀ =0 , когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r=0,4 м и R=0,8 м.

При движении грузов угол изменяется по закону , а угол по закону . В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах.

Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины , указанной в таблице в столбце «Найти», т.е. и , где x₃- координата центра С₃ плиты ( зависимость определяет закон движения плиты ), N- полная нормальная реакция направляющих.

Указания: Задача Д 1- на применение теоремы о движении центра масс. При этом для определения составить уравнение в проекциях на горизонтальную ось Х, а для определения N- на вертикальную ось У.

Таблица Д1