І ітерація

Вибираємо точку, що належить множині допустимих планів задачі. Розглянемо, наприклад, точку .

Визначимо градієнт цільової функції:

.

В точці обчислюємо значення градієнта:

.

Використовуючи розраховане значення градієнта, записуємо і вводимо нову цільову функцію: . Маємо таку задачу лінійного програмування:

.

Розв’язуючи цю задачу симплексним методом, знаходимо її оптимальний план: .

Знайдемо новий допустимий план задачі, використовуючи формулу для визначення координат наступної точки.

Визначаємо координати точки Х₁:

, ,

Знайдемо крок такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х₁, х₂, які виражені через , у цільову функцію :

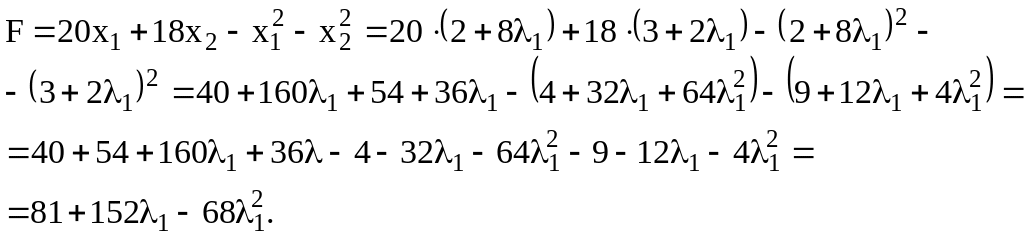
Отримали функцію, що залежить від . Знайдемо значення , за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:

Оскільки , то беремо . Тоді наступна точка Х₁ має координати:

.

Для знайденої точки обчислюємо значення цільової функції: .

Іі ітерація

Узявши точку , обчислюємо значення градієнта в ній:

Використовуючи розраховане значення градієнта, вводимо нову цільову функцію: . Отримуємо таку задачу лінійного програмування:

.

Розв’язавши її симплексним методом, отримуємо оптимальний план: .

За формулою визначаємо координати наступної точки наближення.

Визначаємо координати точки Х₂:

,

.

Знайдемо такий крок λ₂, за якого досягається максимальне значення цільової функції:

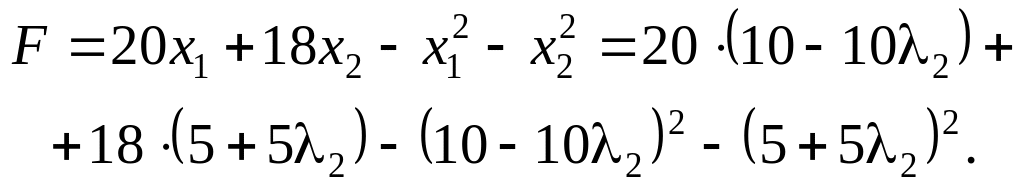
Матимемо .

Обчислимо координати наступної точки Х₂:

Для знайденої точки значення цільової функ­ції дорівнює: .

Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку і переконуємося, що значення цільової функції знову зростає: .

На IV ітерації розраховуються координати точки , для якої .

V ітерація

Узявши точку , обчислюємо значення градієнта в ній:

.

Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію: і маємо таку задачу лінійного програмування:

,

.

Розв’язавши цю задачу, отримаємо значення оптимального плану , тобто повертаємося до попереднього значення. Отже, точку з координатами вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.

8. Розвязання задач нелінійного програмування на пеом

Як вже відмічалось на початку теми, на відміну від задач лінійного програмування, не існує універсального методу розв’язання задач нелінійного програмування. У науковій літературі можна знайти принаймні 10-15 методів нелінійної оптимізації, кожний з яких, як правило, ефективно „працює” для деякого класу моделей нелінійного програмування і є неефективним для інших. Інструмент Поиск решения табличного процесора MS Excel для розв’язання задач нелінійного програмування використовує тільки один метод – метод приведених градієнтів, тому з практичної точки зору важливо знати перспективи розв’язання та особливості застосування цього інструменту для різних класів моделей нелінійного програмування і відповідних задач нелінійного програмування.

Виходячи з цього, усі нелінійні оптимізаційні моделі можна поділити на два класи:

• моделі, які піддаються оптимізації за допомогою інструменту Поиск решения;

• моделі, які можна спробувати оптимізувати за допомогою інструменту Поиск решения.

Моделі першого класу зустрічаються у таких задачах нелінійного програмування, як:

• задачі квадратичного програмування;

• задачі опуклого програмування.

Моделі другого класу, які ще прийнято називати суттєво нелінійними притаманні задачам нелінійного програмування загального виду, для яких властивості увігнутості або випуклості математичної моделі відсутні.

Множники Лагранжа мають цікаву і важливу економічну інтерпретацію. Ці множники в моделях нелінійного програмування інтерпретуються практично як тіньові ціни в моделях лінійного програмування. Іншими словами, в точці оптимальності значення i–го множника Лагранжа є миттєвою швидкістю зміни оптимального значення цільової функції при зростанні значення правої частини i–го обмеження задачі при незмінності усіх інших даних задачі. Використовуючи економічну термінологію, можна сказати, що і–й множник Лагранжа відображує граничну вартість i–го ресурсу і вимірюється у тих одиницях, які визначаються як відношення одиниці вимірювання цільової функції до одиниці вимірювання правої частини i–го обмеження.

Як і тіньові ціни (двоїсті оцінки) у моделях лінійного програмування, додатне значення множника Лагранжа показує, що збільшення правої частини деякого обмеження-нерівності призведе до зростання оптимального значення цільової функції, а від’ємне значення множника Лагранжа показує, що збільшення правої частини деякого обмеження-нерівності – призведе до зменшення оптимального значення цільової функції. Але на відміну від задач лінійного програмування в задачах нелінійного програмування нічого не можна сказати щодо діапазону зростання або зменшення правої частини деякого обмеження, для якого дане значення множника Лагранжа є незмінним. Звичайною, як правило, є ситуація, коли множник Лагранжа сам змінюється разом із зміною правої частини. Але це не заважає використовувати його для оцінювання впливу зміни правої частини деякого обмеження на значення цільової функції.

Значення нормованого градієнта у звіті Устойчивость для моделей нелінійного програмування інтерпретується аналогічно значенню нормованої вартості для задач лінійного програмування (див. 2.3.1).

25