6. Опукле програмування

Найбільш вивченими і обґрунтованими задачами є задачі опуклого програмування, тобто задачі математичного програмування, в яких цільова функція є опуклою (або вгнутою), а область допустимих розв’язків – опуклою множиною. Перевагою задач опуклого програмування є те що цільова функція завжди має екстремум, причому глобальний.

Означення 1. Функція , що задана на опуклій множині , називається опуклою, якщо для будь-яких двох точок і довільного виконується співвідношення

.

Означення 2. Функція , що задана на опуклій множині , називається вгнутою, якщо для будь-яких двох точок і довільного виконується співвідношення

.

Якщо функція - опукла, то функція - вгнута.

Загальна постановка задачі опуклого програмування має вигляд:

, (16)

, , (17)

, (18)

де - вгнута, а — опуклі функції. Якщо задача опуклого програмування задається на мінімум, то функція мусить бути опуклою.

Множина допустимих планів задачі, що визначається системою (17), є опуклою. Будемо вважати надалі, що область допустимих розв’язків (17) – (18) задачі (16) – (18) не порожня і обмежена.

Терема 1. Довільний локальний максимум (мінімум) задачі опуклого програмування є глобальним максимумом (мінімумом).

Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).

Означення 3. Множина допустимих планів (17) – (18) задовольняє умову регулярності, якщо існує хоча б одна точка з області допустимих планів така, що .

У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа. Функція Лагранжа для задачі (16)—(18) має вид:

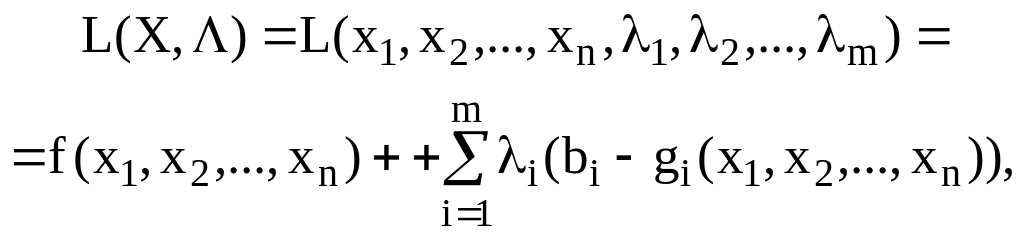(19)

де — множники Лагранжа.

Означення4. Точка називається сідловою точкою функції Лагранжа якщо

для всіх і .

Теорема 2. (теорема Куна-Таккера). Нехай для області допустимих розв’язків задачі опуклого програмування (16) – (18) виконується умова регулярності. План буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор , що пара - сідлова точка функції Лагранжа.

Використовуючи теорему Куна — Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування:

(І)  , ; (20)

(ІІ)  , ; (21)

(ІІІ)  , ; (22)

(IV)  , . (23)

Для задачі мінімізації,де всі функції диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (21) та (23).

Зауваження 1. Теорему Куна – Танкера можна розглядати як узагальнення теореми двоїстості у лінійному програмуванні, а множники Лагранжа – як двоїсті оцінки.

Зауваження 2. Умови Куна – Танкера мало придатні для знаходження оптимального розв’язку, вони лише характеризують розв’язок, тобто дають можливість перевірити деякий розв’язок на оптимальність.

Розглянемо тепер задачу квадратичного програмування, яка є окремим випадком задачі опуклого програмування. Специфіка цієї задачі полягає утому, що система обмежень є лінійною, а цільова функція квадратичною.

Означення 5. Квадратичною формою відносно змінних називається числова функція від цих невідомих вигляду

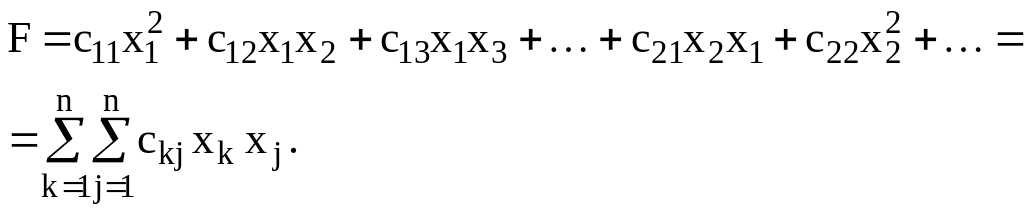
Означення 6. Квадратична форма називається додатньо (від’ємно) – визначеною, якщо для усіх значень змінних , окрім .

Означення 7. Квадратична форма називається додатньо (від’ємно) – напіввизначеною, якщо для будь-якого набору значень змінних і, крім того існує такий набір змінних , де не всі значення змінних одночасно дорівнюють нулю, так що .

Теорема 3. Квадратична форма є опуклою функцією, якщо вона додатньо-напіввизначена, і є вгнутою функцією, якщо вона від’ємно-напіввизначена.

Постановка задачі квадратичного програмування має вигляд:

, ( 24 )

, ( 25 )

, ( 26 )

де - від’ємно (додатньо) – напіввизначена квадратична форма.

Функція Лагранжа для сформульованої задачі квадратичного програмування запишеться у вигляді:

.

Якщо функція Лагранжа має сідлову точку , то в цій точці виконуються співвідношення (20) – (23). Ввівши тепер додаткові змінні і , що перетворюють нерівності (20) і (22) у рівності, перепишемо вирази (20) – (23) для задачі квадратичного програмування наступним чином:

, ( 27 )

, ( 28 )

, ( 29 )

, ( 30 )

. ( 31 )

Щоб знайти розв’язок задачі квадратичного програмування (24) – (26), необхідно визначити невід’ємний розв’язок системи лінійних рівнянь (27) – (28), що задовольняє умовам (29) і (30). Цей розв’язок можна відшукати на основі методу штучного базису(М – методу). Через скінчене число кроків можна отримати або оптимальний план, або встановити нерозв’язність вихідної задачі.