5. Класичний метод оптимізації. Метод множників Лагранжа

5.1. Задачі на безумовний екстремум

Розглянемо задачу (1) – (2) , якщо на змінні не накладаються умови обмежень. У теорії дослідження функцій такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.

Нагадаємо, що необхідна умова існування локального екстремуму функції формулюється так: для того, щоб точ­ка була точкою локального екстремуму, необхідно, щоб функція була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними у цій точ­ці дорівнювали нулю:

, ( 9 )

де - градієнт функції F , що визначається наступним чином:

, де . ( 10 )

Точка називається критичною.

Щоб визначити чи критичні точки є точками екстремуму, необхідно дослідити в них частинні похідні другого порядку. Для функції запишемо матрицю Гессе вигляду

, ( 11 )

яка складається з частинних похідних другого порядку. Оскільки для неперервно-диференційованої функції мішані похідні рівні, тобто , то матриця Н – симетрична.

Головні мінори матриці Н позначимо таким чином:

,

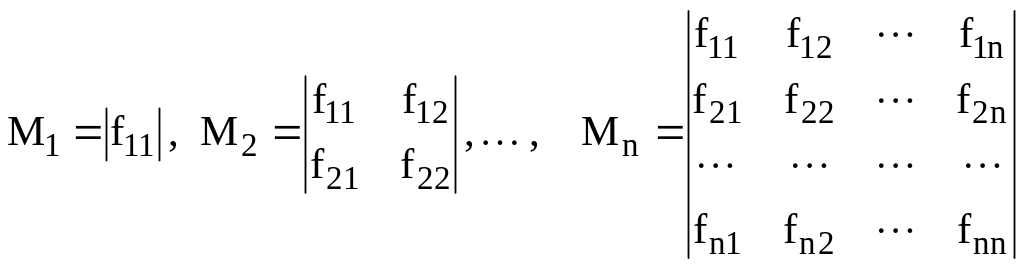де - значення частинної похідної другого порядку функції F в критичній точці .

Достатня умова існування локального екстремуму формулюється так: для того, щоб критична точка була точкою локального екстремуму, достатньо, щоб функ­ція була визначена в околі критичної точки та мала в цій точці неперервні частинні похідні другого порядку.

При цьому якщо всі головні мінори , то точка - точка локального мінімуму. Якщо головні мінори почергово міняють знак, починаючи з мінуса і т.д), то точка - точка локального максимуму.

Проаналізувавши всю область допустимих розв’язків, можна виділити серед локальних екстремумів найбільший і найменший, які й будуть глобальними.

5.2. Метод множників Лагранжа

Розглянемо тепер задачу (1) – (2) , якщо на змінні накладаються умови обмежень у вигляді рівностей:

( 12 )

, , ( 13 )

де функції і двічі неперервно диференційовані функції.

У курсі математичного аналізу задача (12) – (13) називається задачею на умовний екстремум або класичною задачею оптимізації. Умова (13) називається рівнянням зв’язку. Для розв’язання такої задачі використовується метод множників Лагранжа.

Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.

Для знаходження розв’язку задачі (12) – (13) замінимо цільову функцію (13) на іншу. Ця функція називається функцією Лагранжа і має такий вигляд:

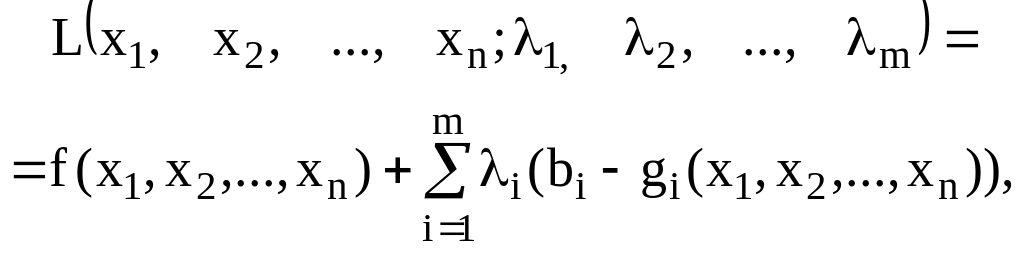(14)

де — деякі невідомі величини, що називаються множниками Лагранжа.

Тоді відшукання умовного екстремуму задачі (12) – (13) зводиться до знаходження безумовного екстремуму функції Лагранжа (14). Знайдемо частинні похідні цієї функції і прирівняємо їх до нуля:

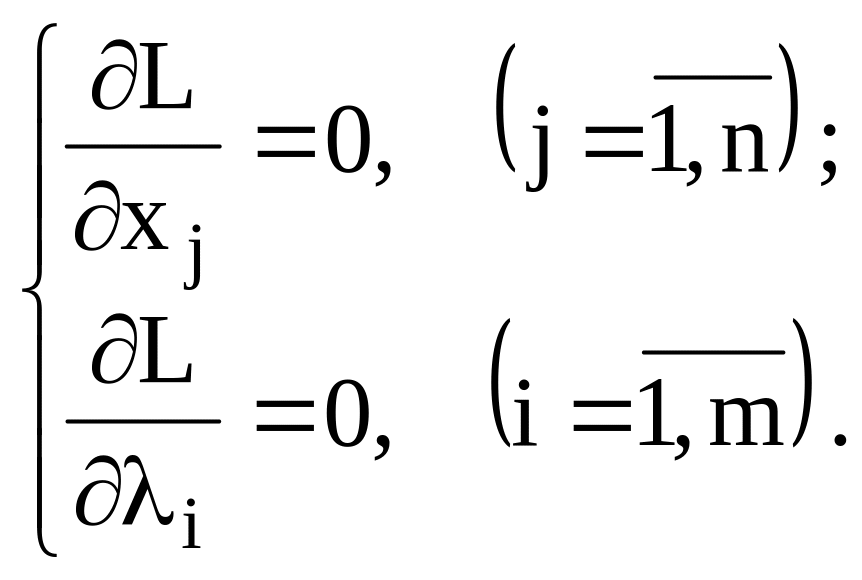
або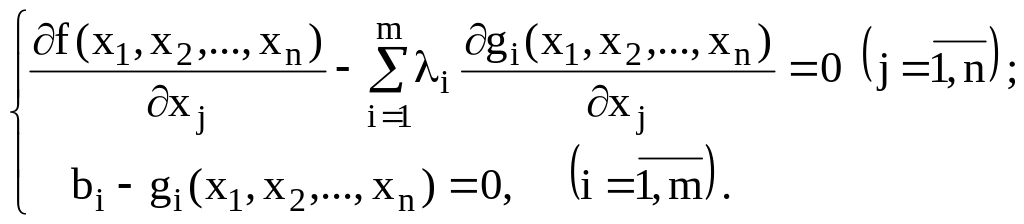 (15)

Друга група рівнянь системи (15) забезпечує виконання умов (13) початкової задачі нелінійного програмування.

Система (15), як правило, нелінійна. Розв’язками її є і — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (12), (13) або можуть бути точками перегину (сідловими точками).

Для діагностування стаціонарних точок і визначення типу екст­ремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій існують другі частинні похідні і вони неперервні). Перевірка виконання достатніх умов екстремуму виконується так само, як і у розглянутому вище випадку безумовного екстремуму.