3. Класифікація задач нелінійного програмування. Загальна характеристика методів розв’язання задач нелінійного програмування.

а) класичні задачі оптимізації:

( 3 )

, ( , ( 4 )

де функції і повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.

б) задачі опуклого програмування – це задачі, в яких цільова функція і функції обмежень є опуклими (вгнутими) функціями.

в) сепарабельні задачі нелінійного програмування:

, ( 5 )

; ( 6 )

г) квадратичні задачі нелінійного програмування :

, ( 7 )

; ( 8 )

Найбільш вивченими серед задач нелінійного програмування є задачі з нелінійною цільовою функцією та лінійними обмеженнями.

Для розв’язування задач нелінійного програмування використовуються графічні та аналітичні методи.

Аналітичні методи поділяються на:

• прямі методи;

• непрямі методи.

Прямими методами оптимальні розв’язки знаходять у напрямку найшвидшого збільшення (або зменшення) значення цільової функції. До прямих методів належать градієнтні методи.

Непрямі методи полягають у зведенні задачі до такої, знаходження екстремуму якої вдається спростити. До непрямих методів відносяться методи сепарабельного та квадратичного програмування.

Що ж стосується класичних задач оптимізації, то вони розв’язуються класичними методами з використанням апарату диференціального числення.6

4. Геометрична інтерпретація задачі нелінійного програмування. Графічний метод розв’язання задач нелінійного програмування

Геометрично цільова функція (2) визначає деяку поверхню, а обмеження (1) — допустиму підмножину n-вимірного евклідового простору. Знаходження оптимального розв’язку задачі нелінійного програмування зводиться до відшукання точки з допустимої підмножини, в якій досягається поверхня найвищого (найнижчого) рівня.

Якщо цільова функція неперервна, а допустима множина розв’язків замкнена, непуста і обмежена, то глобальний максимум (мінімум) задачі існує.

Алгоритм знаходження розв’язку задачі нелінійного програмування графічним способом

1. Знаходиться область допустимих розв’язків, що визначається співвідношеннями ( 1 ). Якщо вона порожня, то задача не має розв’язків.

2. Будуємо лінії рівня цільової функції 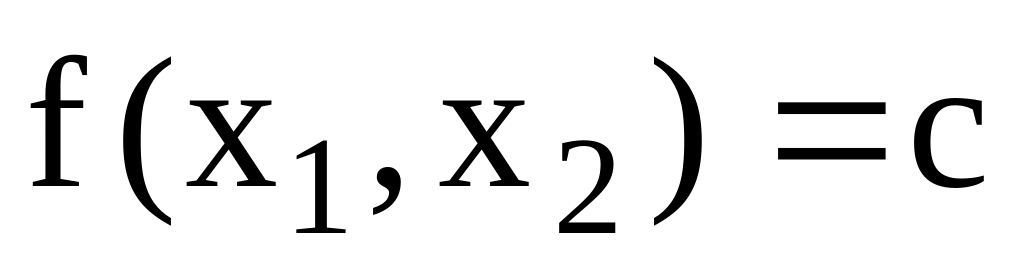, де с – стала величина.

3. Визначаємо лінії найвищого (найнижчого) рівня або встановлюємо нерозв’язність задачі із-за необмеженості функції (2) зверху (знизу) на множині допустимих розв’язків.

4. Знаходимо точку області допустимих розв’язків, через яку проходить лінія найвищого (найнижчого) рівня, і обчислюємо у ній значення цільової функції ( 2 ).

Розглянемо приклад геометричного способу розв’язування задачі нелінійного програмування.

З найти мінімальне і максимальне значення функції:

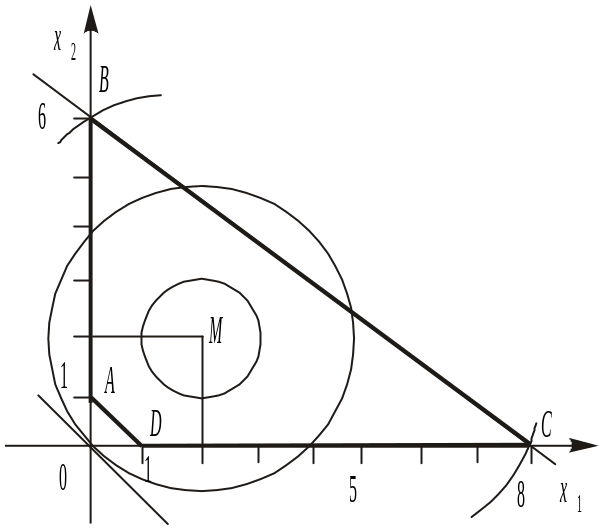
Рис. 8.1

за умов:

.

Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 8.1). Геомет­рично цільова функція являє собою коло з центром у точці М (2; 2), квадрат радіуса якого . Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція F має два локальних мак­симуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:

,

.

Оскільки , то точка С (8; 0) є точкою глобального максимуму.

Очевидно, що найменший радіус , тоді:

. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.

Зазначимо, що в даному разі точка, яка відповідає оптимальному плану задачі (мінімальному значенню функціонала), знаходиться всередині багатокутника допустимих розв’язків, що в задачах лінійного програмування неможливо.

Знайти мінімальне значення функції:

за умов:

.

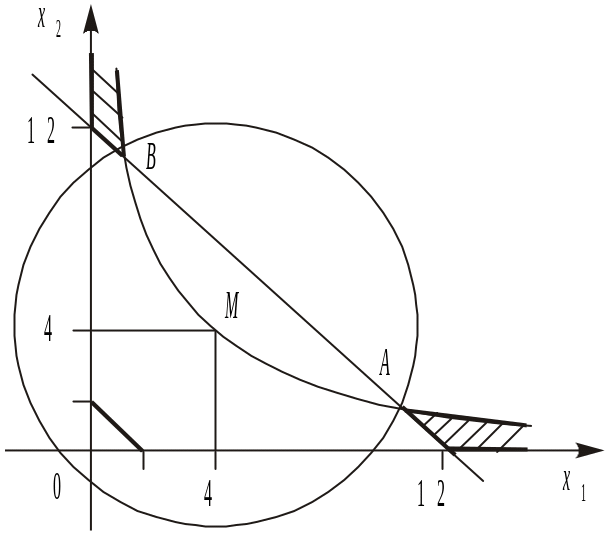
Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених звер­ху (рис. 8.2). Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція F має два локальних мінімуми: в точці А ( ), і в точці В ( ).

З

Рис. 8.2.

начення цільової функції в цих точках однакове і дорівнює:

.

Отже, маємо два альтернатив­ні оптимальні плани.

Даний приклад ілюструє ще одну особливість задач нелінійного програмування: на від­міну від задач лінійного програмування багатогранник допустимих розв’язків задачі нелінійного програмування не обов’язково буде опуклою множиною.