
- •1. Вводные сведения 16
- •Тема 1. Вводные сведения
- •Предмет колориметрии
- •Свет – электромагнитная волна
- •Шкала эмв
- •Тема 2. Элементы геометрической оптики
- •Вводные сведения
- •Четыре закона геометрической оптики
- •Принцип Ферма
- •Закон преломления
- •Тема 3. Тонкие линзы
- •Вводные сведения
- •Построение изображения, даваемого линзой
- •Тема 4. Спектр светового излучения. Цвет
- •Спектральный состав излучения
- •Формирование цвета предметов
- •Методика оценки цвета излучения с непрерывным спектром
- •Тема 5. Источники света. Элементы фотометрии
- •Основные виды источников излучения
- •Стандартные источники излучения
- •Элементы фотометрии
- •Тема 6. Восприятие цвета
- •Глаз – орган восприятия цвета
- •Трехкомпонентная теория зрения.
- •Адаптация зрения
- •Контраст цветов
- •Тема 7. Характеристики цвета. Цветочувствительность глаза
- •Психологическая система описания цветов
- •Психофизическая система характеристики цвета
- •Цветочувствительность глаза
- •Тема 8. Методы образования цвета. Законы Грассмана
- •Аддитивный синтез цвета
- •Законы Грассмана
- •1 Закон
- •2 Закон
- •3 Закон (Закон аддитивности цвета)
- •С убстрактивный синтез цвета
- •Прозрачные среды
- •Непрозрачные среды
- •Тема 9. Теоретические основы измерения цветов
- •Система описания цветов rgb (1931г)
- •Графическое представление цветов в системе rgb
- •Система описание цветов xyz (1931г)
- •4. Цветовой график системы xyz
- •Приложение Удельные координаты монохроматических излучений в системе xyz
- •Литература
Тема 3. Тонкие линзы
Вводные сведения
Л инзой
называется оптически прозрачное тело
(обычно стеклянное), ограниченное двумя
криволинейными поверхностями или одной
плоской и одной криволинейной поверхностью.
инзой
называется оптически прозрачное тело
(обычно стеклянное), ограниченное двумя
криволинейными поверхностями или одной
плоской и одной криволинейной поверхностью.
Ч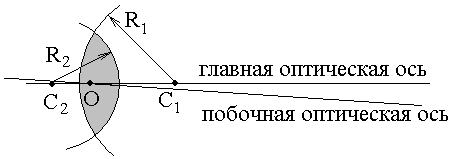 аще
всего поверхности линзы имеют форму
сферы, хотя для специальных применений
изготавливают параболические или даже
цилиндрические линзы.
аще
всего поверхности линзы имеют форму
сферы, хотя для специальных применений
изготавливают параболические или даже
цилиндрические линзы.
Рис. 3.1 Линза: С1 и С2 – центры сферических поверхностей, R1 и R2 – радиусы кривизны сферических поверхностей (для плоской поверхности считают R =)
Т онкой
линзой называется линза, толщина
которой мала по сравнению с радиусами
кривизны её поверхностей.
онкой
линзой называется линза, толщина
которой мала по сравнению с радиусами
кривизны её поверхностей.
Главной оптической осью линзы называется прямая, проходящая через центры кривизны сферических поверхностей линзы С1 и С2.
Точка линзы, проходя через которую луч света не меняет своего направления, называется оптическим центром линзы 2.
Любая прямая, проходящая через оптический центр линзы под углом к ее главной оптической оси называется побочной оптической осью.
По своим свойствам, линзы подразделяются на два класса:
Собирающие линзы (или положительные), обозначаются «+». Критерий: пучок параллельных лучей собирается линзой «в точку». Для стеклянной линзы в пустоте/воздухе это эквивалентно утверждению, что средняя часть линзы толще ее краев.
Рассеивающие линзы (или отрицательные), обозначаются «–». Критерий: пучок параллельных лучей после линзы «расходится веером». Для стеклянной линзы в пустоте/воздухе это эквивалентно утверждению, что края линзы толще ее средней части
Рассмотрим ход световых лучей, падающих на линзу параллельно главной оптической оси. После прохождения через собирающую линзу, лучи сойдутся в одной точке, которая называется главный фокус линзы. Эта точка всегда лежит на главной оптической оси. Точно такие же лучи света после прохождения через рассеивающую линзу станут расходиться – наблюдателю они покажутся исходящими из мнимого главного фокуса линзы.
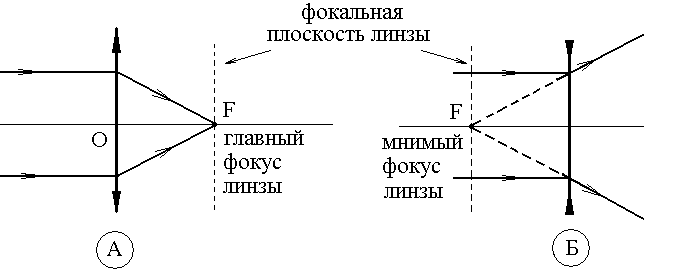 Рис.
3.2 Прохождение лучей света через
линзу. А - собирающая линза, Б -
рассеивающая линза
Рис.
3.2 Прохождение лучей света через
линзу. А - собирающая линза, Б -
рассеивающая линза
Е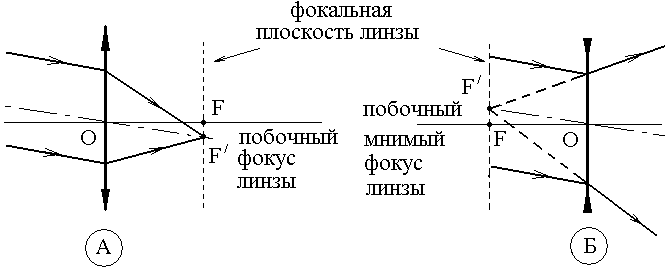 сли
падающие лучи света не параллельны
главной оптической оси линзы, то вместо
главного фокуса необходимо использовать
так называемый «побочный фокус» (см.
рис 3.3)
сли
падающие лучи света не параллельны
главной оптической оси линзы, то вместо
главного фокуса необходимо использовать
так называемый «побочный фокус» (см.
рис 3.3)
Рис. 3.3 Нахождение побочного фокуса линзы. А - собирающая линза, Б - рассеивающая линза
Расстояние от главного фокуса линзы (точка F) до её оптического центра (точка О) называется «главное фокусное расстояние» (f) и измеряется в метрах [м]. Величина, обратная фокусному расстоянию, называется «оптическая сила линзы» (D) и измеряется в «диоптриях» [дп]:
D=1/f (3.1)
Отметим, что в выражение (3.1) и в другие формулы геометрической оптики, величины f и D входят со знаком: для собирающих линз f>0 и D>0. для рассеивающих линз f<0 и D<0.
Оптическая сила линзы D зависит от свойств материала, из которого она изготовлена, от радиусов кривизны её поверхностей R1 и R2 , а так же от оптических свойств окружающей среды:
![]() , (3.2)
, (3.2)
где R1 и R2 – радиусы кривизны (в метрах), которые подставляются формулу в соответствии со следующим правилом знаков: Ri > 0 – если центр кривизны соответствующей поверхности «находится внутри линзы» и Ri < 0 – в противном случае.
Сделаем два важных замечания:
При складывании тонких линз друг с другом их оптические силы складываются:
Dсумма = D1+D2 (3.3)
Величина nлинза в формуле (3.2) зависит от длины волны света: nлинза= nлинза(), поэтому для разных волн оптическая сила линзы D будет не одинакова – для «длинных волн» D всегда несколько меньше, чем для «коротких» (вспомните призму).
